大数据与贝叶斯理论在足球比赛分析与预测中的应用

随着科技的不断进步，大数据分析在各个领域的应用也越来越广泛，其中包括体育竞技。足球比赛作为全球最受欢迎的运动之一，也借助大数据和贝叶斯理论来进行模型分析和预测。本文将通过结合贝叶斯定义和泊松分布模型，探讨大数据如何在分析和预测足球比赛中发挥作用。

贝叶斯定理是关于随机事件A和B的条件机率(或边缘机率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。

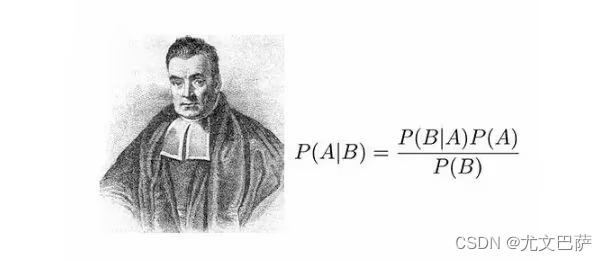
贝叶斯根据大量类似的经验总结的公式:P(Y|X)=P(X,Y)/P(X),对应这个例子就是P(X)是今天下雨的概率,P(X,Y)是今天和明天都下雨的概率,P(Y|X)是今天下雨的情况下明天下雨的概率。

首先，我们需要了解贝叶斯定义以及泊松分布模型在统计学中的应用。贝叶斯定义是由英国统计学家托马斯·贝叶斯提出的一种用于更新和修正概率的方法。该方法将主观的先验概率与新的证据相结合，得出更准确的后验概率。而泊松分布模型则是一种离散概率分布，用于描述时间或空间上独立事件发生次数的概率。

大数据的优势在于它可以提供庞大的数据样本，这意味着我们可以从海量的数据中挖掘出有用的信息，并找到隐藏在数据中的模式和规律。在足球比赛中，我们可以根据球队的历史数据进行分析，例如近期的胜率、进球数、失球数等等。这些数据可以用来生成泊松分布模型的参数，进而用于预测未来比赛的结果。

以一支球队的进球数为例，我们可以利用贝叶斯定义并结合历史数据，计算出该队伍在下一场比赛中进球的概率分布。假设该队在过去的10场比赛中共进了15个球，那么我们可以将泊松分布模型应用于这组数据。根据泊松分布的特性，我们可以通过计算平均值来估计进球的期望数量。如果我们假设进球的期望为1.5个，那么我们可以得到不同进球数的概率分布，例如进0个球的概率为0.2231，进1个球的概率为0.3347，进2个球的概率为0.251，以此类推。

通过贝叶斯定义，我们可以将新的证据与先验概率相结合，从而修正和更新进球数的后验概率。比如，如果我们得知对手球队的防守实力很强，那么我们可以根据先前的进球概率分布和新的证据来计算修正后的后验概率。这样，我们就可以得到一个更准确的进球预测结果。

除了分析进球数外，大数据还可以用于分析其他的足球比赛指标，如控球率、传球成功率、犯规次数等。通过对这些指标进行统计分析，我们可以建立更完整的模型，对比赛结果进行全面的预测。

然而，需要注意的是，大数据和贝叶斯定义并不能100%准确地预测比赛结果。足球比赛是一项复杂的活动，受到众多因素的影响，包括球员状态、战术安排、环境条件等等。因此，尽管大数据和贝叶斯定义可以提供有用的参考，但最终的结果可能仍然取决于各种未知因素。

综上所述，大数据结合贝叶斯定义和泊松分布模型可以在足球比赛分析和预测中发挥重要作用。它们可以帮助我们从历史数据中提取有用的信息，并建立相应的模型来预测比赛结果。然而，我们仍然需要谨慎对待这些预测结果，并意识到其局限性。在未来的研究中，我们可以进一步探索其他统计模型和算法，以提高对足球比赛结果的准确性。
点击获取软件详细教程
软件截图：




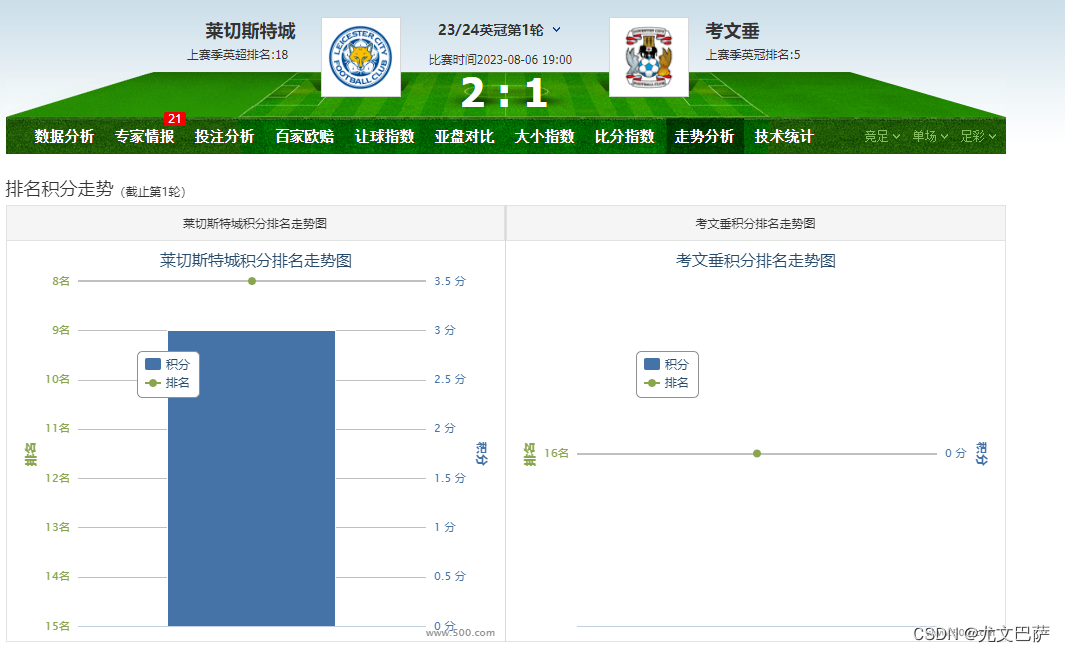
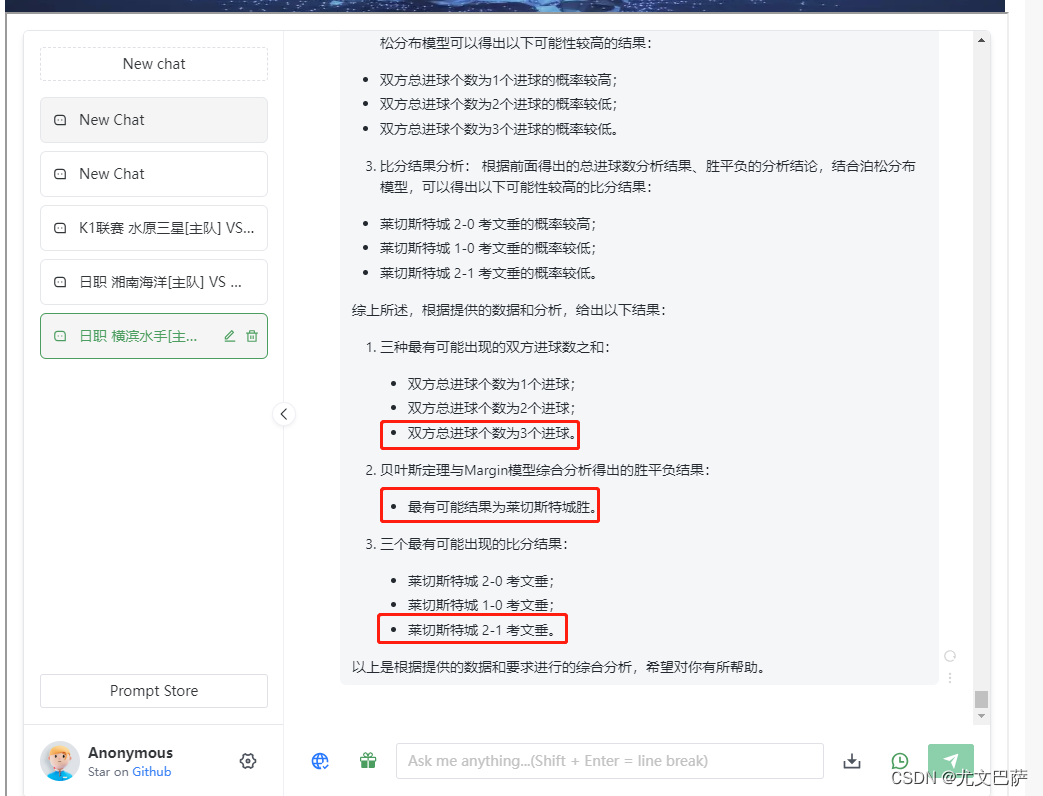
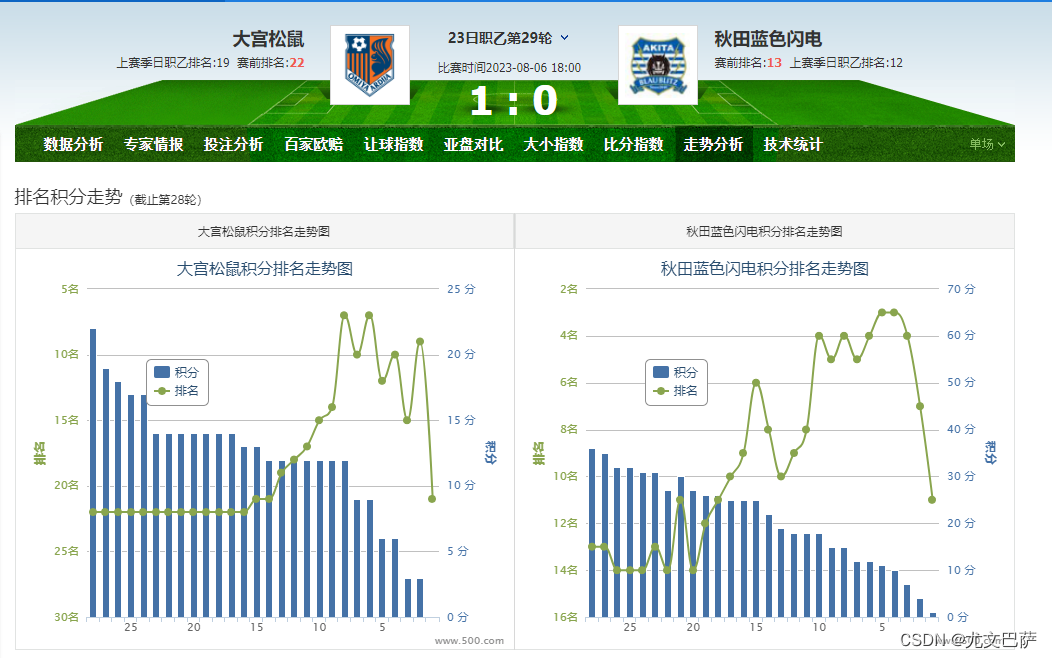
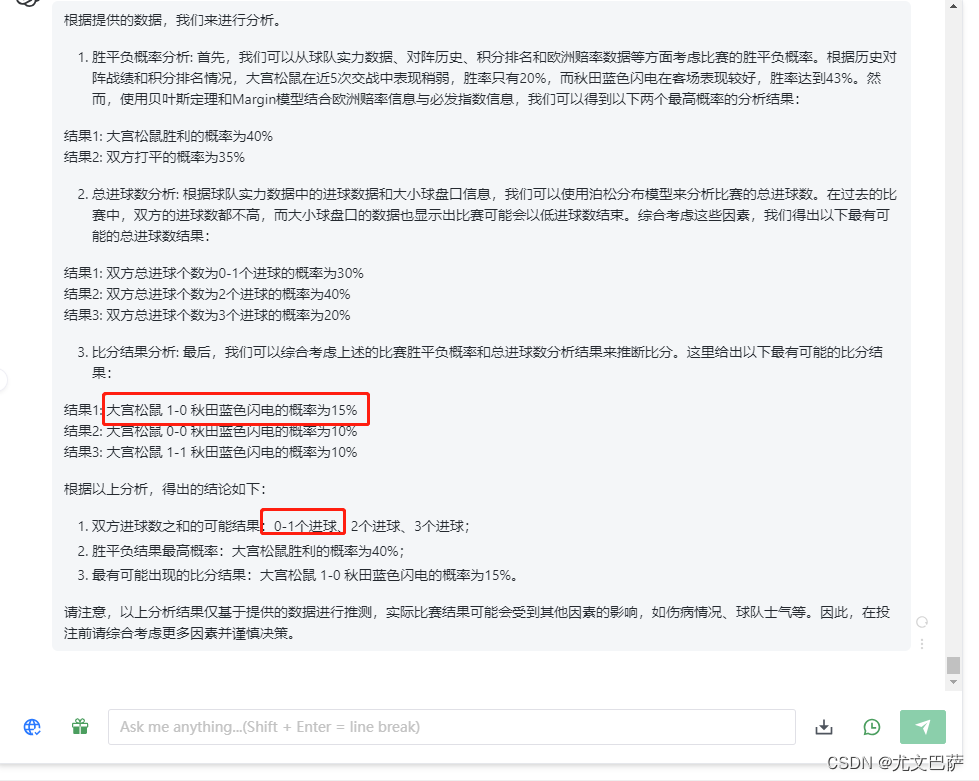
案例就分享到这，凡事没有绝对，欢迎联系作者交流。