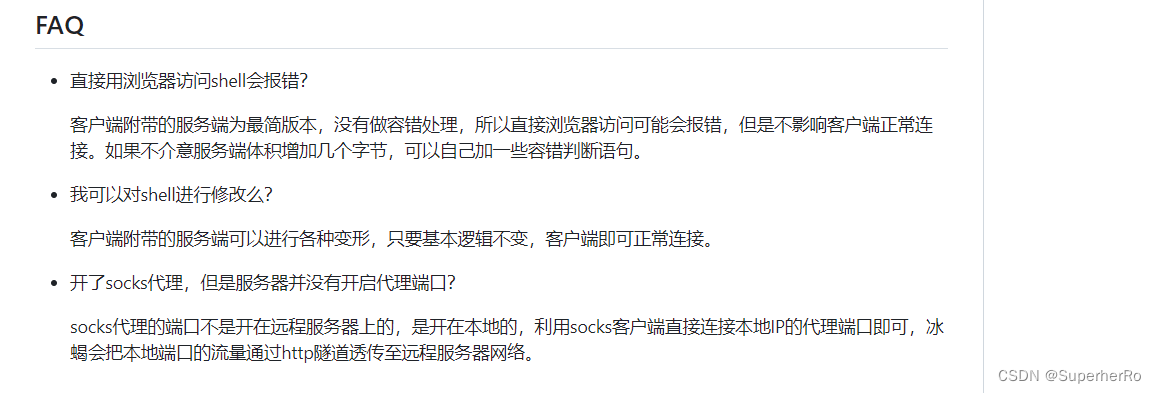
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
这种题型一般都是按照dfs进行遍历查找,因为一个位置上有8种选择

所以我们应该提前的声明两个数组,一个数组中放x坐标,一个数组放y坐标
//设置方向 上右下左
int[] xnum={-1,0,1,0};
int[] ynum={0,1,0,-1};
我觉得这东西和扫雷是一个性质

将雷区看做是水域,数字区看成是我们的陆地,以当前节点为中心,往周围漫射(一条路走到底),但是如果
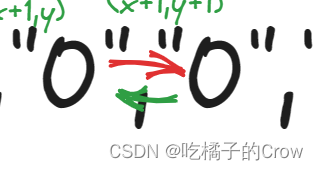
如果我们从A点到B点,如果不加限制的话,我们同样也能从B点到A点,这样就有可能能造成死循环,或者使得最后的效率变慢,所以我们可以采用两种方式
第一种方式:额外的维护一个visited数组,对访问过的地域进行标记
visited=new boolean[row][column];第二种方式:将访问过的陆地给填充成海域,不需要其他额外的操作
grid[i][j]='0';如果还不理解题,还可以这样想,假如题目数组中1组成的是由纯净水的组成的管道,我们每次遍历一个地点就是相当于给这些管道中滴了一滴红墨水,红墨水随着水的流动性,不一会这条管道中的纯净水都会变成红颜色的水
//相当于滴红墨水,需要知道该地点的坐标
private void dfs(char[][] grid, int x, int y) {
} //如果是碰到水域,则停止遍历
if(grid[x][y]=='0'){
return;
}
//是陆地且没有被访问过,进行访问,并以该地点为中心,漫射
if(grid[x][y]=='1'&&!visited[x][y]){
visited[x][y]=true;
//对于漫射的8种选择
for (int i = 0; i <4; i++) {
int newx=x+xnum[i];
int newy=y+ ynum[i];
//越界情况直接继续,不需要执行
if(newx<0||newx>=row||newy<0||newy>=column||visited[newx][newy]){
continue;
}
dfs(grid,newx,newy);
}在判断是否是一个新的岛屿,肯定需要满足两个条件:1.是陆地 2.没有被访问过
//开始连接的岛屿,第一个
if(!visited[i][j]&&grid[i][j]=='1'){
count++;
}碰到新的陆地后,再进行重复的操作
dfs(grid,i,j);
好了,这道题的原理已经讲完,希望对大家能对这道题有一个比较深刻的印象
源码如下:
//设置方向 上右下左
int[] xnum={-1,0,1,0};
int[] ynum={0,1,0,-1};
boolean[][] visited;
int row;
int column;
public int numIslands(char[][] grid) {
//对入参进行判断
if(grid==null||grid.length==0||grid[0].length==0){
return 0;
}
int count=0;
//从每一个点都开始进行遍历
row=grid.length;
column=grid[0].length;
visited=new boolean[row][column];
for (int i = 0; i <row; i++) {
for (int j = 0; j <column; j++) {
//开始连接的岛屿,第一个
if(!visited[i][j]&&grid[i][j]=='1'){
count++;
dfs(grid,i,j);
}
}
}
return count;
}
private void dfs(char[][] grid, int x, int y) {
//如果是碰到水域,则停止遍历
if(grid[x][y]=='0'){
return;
}
if(grid[x][y]=='1'&&!visited[x][y]){
visited[x][y]=true;
for (int i = 0; i <4; i++) {
int newx=x+xnum[i];
int newy=y+ ynum[i];
if(newx<0||newx>=row||newy<0||newy>=column||visited[newx][newy]){
continue;
}
dfs(grid,newx,newy);
}
}
}