前言

本文部分内容参考了深蓝学院的移动机器人运动规划，依此做相关的笔记与整理。

相关代码整理:

1. https://gitee.com/lxyclara/motion-plan-homework/
2. https://github.com/KailinTong/Motion-Planning-for-Mobile-Robots/blob/master
3. https://gitee.com/aries-wu/Motion-plan/blob/main/
4. 链接: https://pan.baidu.com/s/1UtVHRxDq771LfSGK_21wgQ?pwd=rhtp 提取码: rhtp

相关文章：

1. 自动驾驶路径规划——轨迹规划（详解插值法）

介绍

什么是kinodynamic？

$Kinodynamic:Kinematic+Dynamic$

运动学规划问题是综合机器人的运动，同时受到运动学约束（如避开障碍物）和动力学约束（如速度、加速度和力的模量边界）。动力学解是从时间到广义力或加速度的映射。

• Differentially constrained(微分约束)
• Up to force (acceleration)，考虑到力（加速度）

为什么需要kinodynamic？

之前几节介绍的规划算法往往没有考虑到系统的微分约束，状态点之间的连接形成的路线不能直接被用作无人车、无人机的轨迹。

这里可能又会产生新的疑惑？传统的Pipeline通过先规划出一条路径，在通过后端轨迹优化的方式，同样也能得到适用于无人车的轨迹。但是，若在前端不考虑运动学/动力学的约束，完全交由后端的轨迹优化进行，那么后端的负担就会比较大。

规划通常需要以下几点：
• Coarse-to-fine process（流程从粗到细）
• Trajectory only optimizes locally （轨迹优化基于局部的状况）
• Infeasible path means nothing to nonholonomic system（在非完整系统中，一些不可行路径将会毫无意义）

基于kinodynamic的规划算法可以在path finding这一步就可以得到比较理想的轨迹，再在trajectory optimization部分优化时，任务相对轻松一些。

如下图右图无人机规划图所示，若采用单纯的前端不考虑运动学/动力学的规划+后端轨迹优化的方式，规划出的路径是紫色实线，很显然无人机依据这个路径得到最终的轨迹会是紫色虚线部分，相比右侧考虑了kinodynamic的规划，轨迹质量更差，需要无人机通过减速、转向等操作才能进行轨迹跟踪。

同样的，从左图的泊车规划示意图中可以看到轨迹是考虑了车辆的运动学/动力学模型的，车辆无法进行侧向移动（暂时不考虑全向麦轮），若按传统方式进行规划，则毫无意义。

模型示例

详细部分可以参考《PLANNING ALGORITHM》这本书

unicycle model（独轮车模型）

状态方程如下：

$$\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}cos\theta \\ sin\theta \\ 0\end{array}\right)\cdot \nu +\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\cdot \omega$$

独轮车模型对于速度$v$、角速度$\omega$有以下约束：
$$\begin{array}{rl}|v|& \le {\nu }_{\max }\\ |\omega |& \le {\omega }_{\max }\end{array}$$

differential model（两轮差速模型）

状态方程如下：

$$\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}\frac{r}{2}({\omega }_l+{\omega }_r)cos\theta \\ \frac{r}{2}({\omega }_l+{\omega }_r)sin\theta \\ \frac{r}{L}({\omega }_r-{\omega }_l)\end{array}\right)$$$$v=\frac{r}{2}({\omega }_l+{\omega }_r)cos\theta$$$$\begin{array}{r}\omega =\frac{r}{L}({\omega }_r-{\omega }_l)\end{array}$$

其左右轮角速度有以下限制：
$$\begin{array}{rl}|{\omega }_l|& \le {\omega }_{l,max}\\ |{\omega }_r|& \le {\omega }_{r,max}\end{array}$$

Simplified car model (简化车辆模型)

状态方程如下：

$$\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}vcos\theta \\ vsin\theta \\ \frac{r}{L}tan\varphi \end{array}\right)$$

模型	约束
Simple car model
Reeds & Shepp’s car
Dubin’s car

State Lattice Planning

相比较之前的搜索算法，我们需要图中的连接是可行的、符合车辆动力学约束的。

同时，对于图的建立，包括正向连接和反向连接。正向的方法将机器人的控制空间进行离散化；反向的方向则是对周围的状态空间进行离散化。

具体到小车/机器人的控制，可以进行以下描述：

对于一个机器人模型 $\dot{s}=f(s,u)$，假设我已知机器人的初始位置$s_0$，我们可以用以下两种方式对机器人接下来可行的运动进行描述：

1. 选择控制量$u$，确定经历的时间$T$，可以用数值积分的方式正向仿真出机器人接下来的位置。其具有以下的特点

• 正向仿真
• 确定的$u,T$
• 比较容易实现
• 缺乏任务的引导，没有目的性
• 规划效率比较率比较低
  

2. 选定一个状态量$s_f$，确定出从$s_0$到$s_f$之间的轨迹。

• 后向的计算
• 需要计算$u,T$
• 良好的任务引导性
• 比较难以去实现
• 规划效率比较高
  

Sample in control space

示例1

以无人机的模型为例，模型状态变量为$s$，控制输入量为$u$。

$$\text{State: s}=\left(\begin{array}{c}x\\ y\\ z\\ \dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right)\text{Input: }u=\left(\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right)$$

系统的状态方程为：$\dot{s}=A\cdot s+B\cdot u$ ,$A=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]B=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$

高维推广之后，可以得到如下矩阵：$A=\left[\begin{array}{ccccc}0& I_3& 0& \cdots & 0\\ 0& 0& I_3& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 0& I_3\\ 0& \cdots & \cdots & 0& 0\end{array}\right]B=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ I_3\end{array}\right]$

矩阵A是幂零矩阵。

下图是一个基于加速度和jerk的九个平面运动单元从初始点到目标点的移动状态。

上述模型在线性时不变系统中可以如下表述：

所以，当A为幂零矩阵时，状态转移矩阵将可以变得更简洁，后面的高阶项会为0。

$$\begin{array}{l}\text{If matrix A}\in R^{n\times n}\text{is nilpotent,i.e.}{A}^n=0,e^{At}\text{has a closed-form}\\ \text{expression in the form of an}(n-1)\text{degree matrix polynomial in t}.\end{array}$$

PS：在搜索时，只有在有必要的时刻才会进行建图；只有当真正发现节点时，才会建立相应的节点和边；这种带有目的性/启发性的方式，
可以减少计算量。

示例2

以简化后的车辆模型为例：$$\begin{array}{r}\text{State: s}=\left(\begin{array}{c}x\\ y\\ \theta \end{array}\right)\text{Input: }u=\left(\begin{array}{c}v\\ \varnothing \end{array}\right)\\ \text{System equation:}\left(\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right)=\left(\begin{array}{c}v\cdot cos\theta \\ v\cdot sin\theta \\ \frac{r}{L}\cdot tan\varphi \end{array}\right)\end{array}$$

主要有以下步骤：

1. 对于每一个从搜索树中可以找到的状态$s$
2. 选取一定的控制量$u$
3. 对其在一定的时间段内进行数值积分
4. 若得到的边遇到了障碍物，则排除；若没有则不排除

参考论文：Search-based Motion Planning for Quadrotors using Linear Quadratic Minimum Time Control，Sikang Liu, Nikolay Atanasov, Kartik Mohta, and Vijay Kumar

Sample in state space

示例1

基于Reeds-Shepp Car Model完成，状态空间离散化，根据给定的状态计算控制参数。

参考论文：Generating Near Minimal Spanning Control Sets for Constrained Motion Planning in Discrete State Spaces，Mihail Pivtoraiko and Alonzo Kelly

示例2

建立两层的lattice graph，第一层根据车辆的初始状态以及第一层离散化后的状态进行计算得到轨迹，第二次再次离散化状态空间，再次计算。

参考论文：Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots, Thomas M. Howard Alonzo Kelly

比较

控制空间采样的方式难以得到有效的轨迹，同时自由度有限；状态空间采样的方式计算难度大。

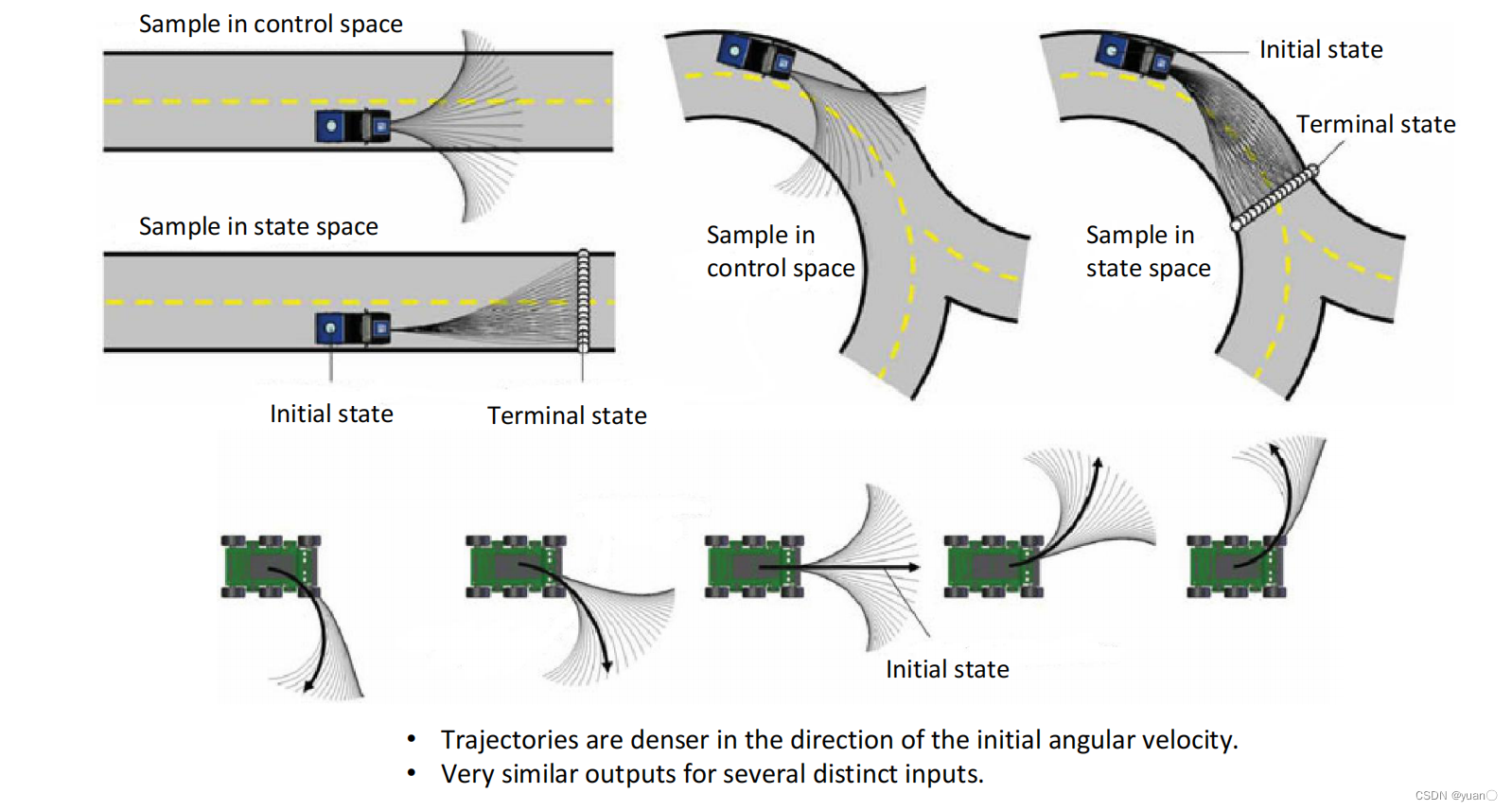
参考论文：State Space Sampling of Feasible Motions for High-Performance Mobile Robot Navigation in Complex Environments, Thomas M. Howard, Colin J. Green, and Alonzo Kelly

Boundary Value Problem (BVP)

BVP是状态空间采样的基础，通常没有通用的解决方案，一般需要复杂的数值优化方法去解决。

首先介绍一下常用的五次多项式插值方法，这部分还可以参考 自动驾驶路径规划——轨迹规划（详解插值法）这篇博文。

首先可以依据起始点、终点状态设置轨迹

之后，利用待定系数法构造多项式，依据边界条件（位置、速度、加速），建立方程组进行求解。

Optimal Boundary Value Problem (OBVP)

论文：A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation, Mark W. Mueller, Markus Hehn, and Raffaello D’Andrea Dynamic Programming and Optimal Control, D. P. Bertsekas
相关博客：庞特里亚金最小值原理解最优控制问题

通过BVP的方式，能求得轨迹的解，但通常不是最优的，因此需要用到OBVP。

首先构建目标函数，对jerk的平方的积分求取最小值：
$$\begin{array}{rl}{J}_{\Sigma }& =\sum _{k=1}^3{J}_k,J_k=\frac{1}{T}{\int }_0^T{j}_k(t{)}^{2}dt.\end{array}$$系统的状态变量是：$s_k=(p_k,v_k,a_k)$,系统的输入是$u_k=j_k$
系统模型为：$\dot{s}=f_s(s_k,u_k)=(v_k,a_k,j_k)$,$k$代表了维度。

之后通过Pontryagin’s minimum principle（庞特里亚金最小值原理）进行求解。

对于Pontryagin’s minimum principle，首先简要介绍一下costate协态$\lambda$，$\lambda =({\lambda }_1,{\lambda }_2,{\lambda }_3)$,可以简单理解为有多少状态量就有多少costate。定义Hamiltonian(汉密尔顿)函数：$$\begin{array}{rl}H\left(s,u,\lambda \right)& \begin{array}{r}=\frac{1}{T}{j}^2+{\lambda }^T{f}_s(s,u)\end{array}\\ & =\frac{1}{T}{j}^2+{\lambda }_{1}v+{\lambda }_{2}a+{\lambda }_{3}j\end{array}$$

Pontryagin’s minimum principle

通常来说，最有问题的目标函数是由终末状态的惩罚项(final state)和从0到T时刻都能量损耗(transition cost)。

接下来，写出系统的汉密尔顿函数。它由状态量$s$, 控制量$u$,以及协态costate$\lambda$组成，$$\begin{array}{rl}H(s,u,\lambda )& =g(s,u)+{\lambda }^{T}f(s,u)\\ \lambda & =({\lambda }_1,{\lambda }_2,{\lambda }_3)\end{array}$$最后求解出最优的状态函数$s^{\ast }$,表示轨迹，以及最优的控制量$u^{\ast }$。

$\lambda (t)$是如下方程的解：$\dot{\lambda }(t)=-{\nabla }_{s}H(s^{\ast }(t),u^{\ast }(t),\lambda (t))$，具有如下边界条件：$\lambda (T)=-\nabla h(s^{\ast }(T))$，h被定义成终末状态的函数。这个公式代表终末状态时间$T$的时候，协态与终末状态中最优的自由量的梯度的和等于0（我们要求上面的问题中的终末状态的p,v,a均达到指定状态，那么这个公式就没了，因为终末状态没有任何自由度）。 最后最优的控制是具有最优状态的汉密尔顿函数的最小值：$\begin{array}{r}{u}^{\ast }(t)=\arg \underset{u(t)}{\min }H(s^{\ast }(t),u(t),\lambda (t))\end{array}$

应用

为了方便，设定$k=1$，则系统模型可以如下表述：$$\dot{s}=f_s(s,u)=(v,a,j)$$其汉密尔顿函数为：$$\begin{array}{rl}H\left(s,u,\lambda \right)& \begin{array}{r}=\frac{1}{T}{j}^2+{\lambda }^T{f}_s(s,u)\end{array}\\ & =\frac{1}{T}{j}^2+{\lambda }_{1}v+{\lambda }_{2}a+{\lambda }_{3}j\end{array}$$对$s$的每个分量$(p,v,a)$进行求得可得：$$\dot{\lambda }=-{\nabla }_{s}H\left(s^{\ast },u^{\ast },\lambda \right)=\left(0,-{\lambda }_1,-{\lambda }_2\right)$$${\lambda }_1$的导数是${\lambda }_2$，${\lambda }_2$的导数是${\lambda }_3$，易得常微分方程组的解为：$$\lambda (t)=\left[\begin{array}{c}\alpha \\ -\alpha t+\beta \\ 0.5\alpha t^2-\beta t+\gamma \end{array}\right]$$配凑系数后可得$$\lambda (t)=\frac{1}{T}\left[\begin{array}{c}-2\alpha \\ 2\alpha t+2\beta \\ -\alpha t^2-2\beta t-2\gamma \end{array}\right]$$接下来求解$u$的最优解，由$u^{\ast }(t)=j^{\ast }(t)=\arg {\min }_{j(t)}H(s^{\ast }(t),j(t),\lambda (t))$可知$u$的最优解与$s^{\ast }(t)$有关。
∵$s^{\ast }(t)=(p^{\ast },v^{\ast },a^{\ast })$
∴汉密尔顿函数可以改写为：$$\begin{array}{rl}H(s,u,\lambda )& =\frac{1}{T}{j}^2+{\lambda }^T{f}_s(s,u)\\ & =\frac{1}{T}{j}^2+{\lambda }_1{v}^{\ast }+{\lambda }_2{a}^{\ast }+{\lambda }_{3}j\end{array}$$此时可得，$H$目前只剩下$j$一个变量，只需对其求得，便可求得控制量$u$:$$\begin{array}{rl}{u}^{\ast }(t)& =j^{\ast }(t)=\arg \underset{j(t)}{\min }H\left(s^{\ast }(t),j(t),\lambda (t)\right)\\ & =\frac{1}{2}\alpha t^2+\beta t+\gamma \end{array}$$现在有了最优的控制表达式，进行一次积分获得$a$,在积分获得$v$,在积分获得$p$，于是$$\begin{array}{r}{\mathrm{s}}^{\ast }(t)=\left[\begin{array}{r}\frac{\alpha }{120}{t}^5+\frac{\beta }{24}{t}^4+\frac{\gamma }{6}{t}^3+\frac{a_0}{2}{t}^2+v_{0}t+p_0\\ \frac{\alpha }{24}{t}^4+\frac{\beta }{6}{t}^3+\frac{\gamma }{2}{t}^2+a_{0}t+v_0\\ \frac{\alpha }{6}{t}^3+\frac{\beta }{2}{t}^2+\gamma t+a_0\end{array}\right]\\ \text{Initial state:}s(0)=(p_0,v_0,a_0)\end{array}$$现在，$s^{\ast }(t)$中的$\alpha 、\beta 、\gamma$还未确定，可以用末尾时刻的边界条件进行确定。令$t=T$，同时代入末尾状态$s_f$时的$p,v,a$的值，可得$$\begin{array}{c}\left[\begin{array}{ccc}\frac{1}{120}{T}^5& \frac{1}{24}{T}^4& \frac{1}{6}{T}^3\\ \frac{1}{24}{T}^4& \frac{1}{6}{T}^3& \frac{1}{2}{T}^2\\ \frac{1}{6}{T}^3& \frac{1}{2}{T}^2& T\end{array}\right]\left[\begin{array}{c}\alpha \\ \beta \\ \gamma \end{array}\right]=\left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]\\ \left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]=\left[\begin{array}{c}{p}_f-p_0-{\mathbf{v}}_{0}T-\frac{1}{2}{\mathbf{a}}_0{T}^2\\ {\mathbf{v}}_f-{\mathbf{v}}_0-{\mathbf{a}}_{0}T\\ {\mathbf{a}}_f-{\mathbf{a}}_0\end{array}\right]\end{array}$$

解方程组得：
$$\left[\begin{array}{c}\alpha \\ \beta \\ \gamma \end{array}\right]=\frac{1}{T^5}\left[\begin{array}{ccc}720& -360T& 60T^2\\ -360T& 168T^2& -24T^3\\ 60T^2& -24T^3& 3T^4\end{array}\right]\left[\begin{array}{c}\Delta p\\ \Delta v\\ \Delta a\end{array}\right]$$

将结果回代目标函数可得：
$$\begin{array}{rl}J& ={\gamma }^2+\beta \gamma T+\frac{1}{3}{\beta }^2{T}^2+\frac{1}{3}\alpha \gamma T^2+\frac{1}{4}\alpha \beta T^3+\frac{1}{20}{\alpha }^2{T}^4\end{array}$$可见，因为$\alpha 、\beta 、\gamma$都与$T$相关，显然可得目标函数$J$只与$T$相关。对$J$求导，就可以求得最优解。

另外：
若在末尾状态时，不完全指定$p,v,a$时，仍然能利用pontryagin’s minimum princple进行计算。利用边界条件$\lambda (t)=-\nabla h(s^{\ast }(t))$,
对于末尾条件确定的情况，$$h(s(T))=\{\begin{array}{llc}0,& ifs=s(T)& \\ \infty ,& otherwise& \end{array}$$并不可微。

对于末尾条件不完全确定的情况，则对未给定的量利用边界条件求偏导进行计算。$$given{s}_i(T),i\in I$$$${\lambda }_j(T)=\frac{\partial h(s^{\ast }(T))}{\partial s_j},forj\ne i$$

论文的附录也给出了相应的情况

其他相关论文：Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots, Thomas M. Howard Alonzo Kelly

Trajectory library（轨迹库）

利用轨迹库，使用cost函数进行评价、打分，作局部路径规划

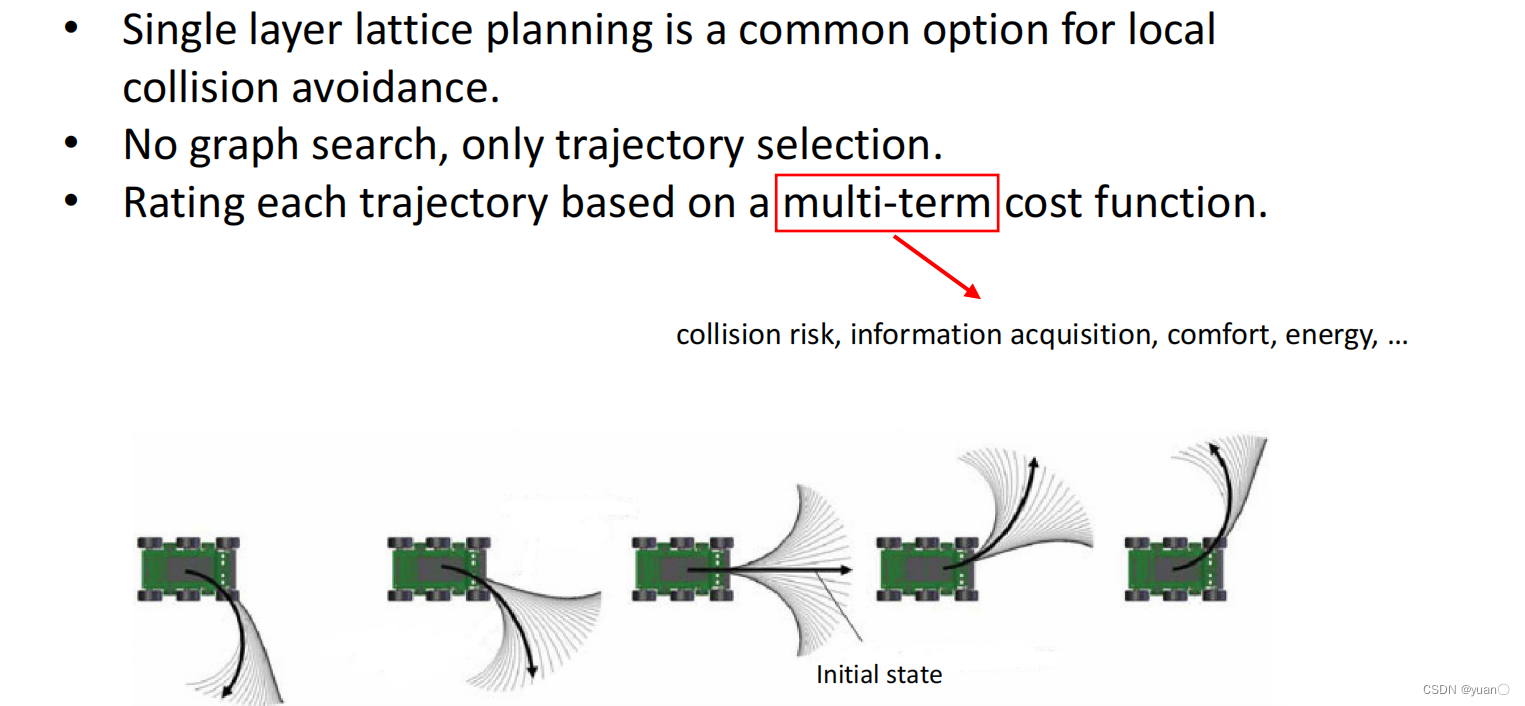
相关论文：Maximum Likelihood Path Planning for Fast Aerial Maneuvers and Collision Avoidance Ji Zhang, Chen Hu, Rushat Gupta Chadha, and Sanjiv Singh

Heuristic design（启发式设计）

通过启发函数加速搜索。（结合考虑动力学不考虑障碍物的估计方法与考虑障碍物不考虑动力学的估计方法。）

论文：Planning Long Dynamically Feasible Maneuvers for Autonomous Vehicles, Maxim Likhachev, Dave Ferguson
论文：Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments, Dmitri Dolgov, Sebastian Thrun, Michael Montemerlo, James Diebel

Planning in Frenet-serret Frame

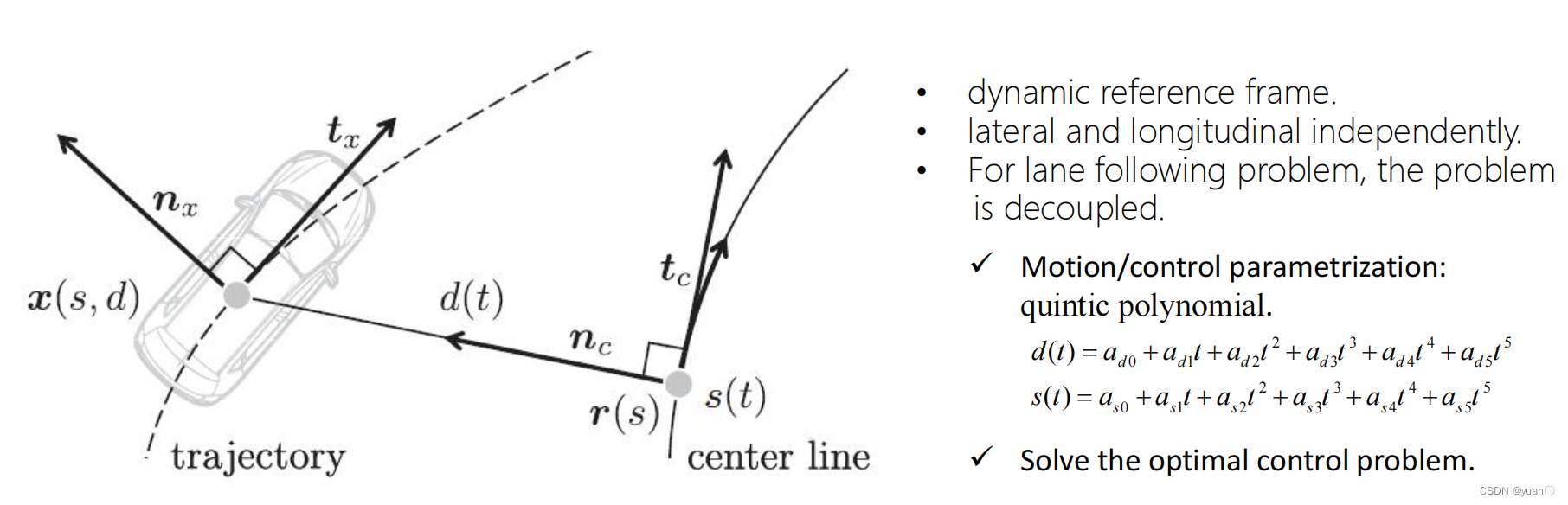
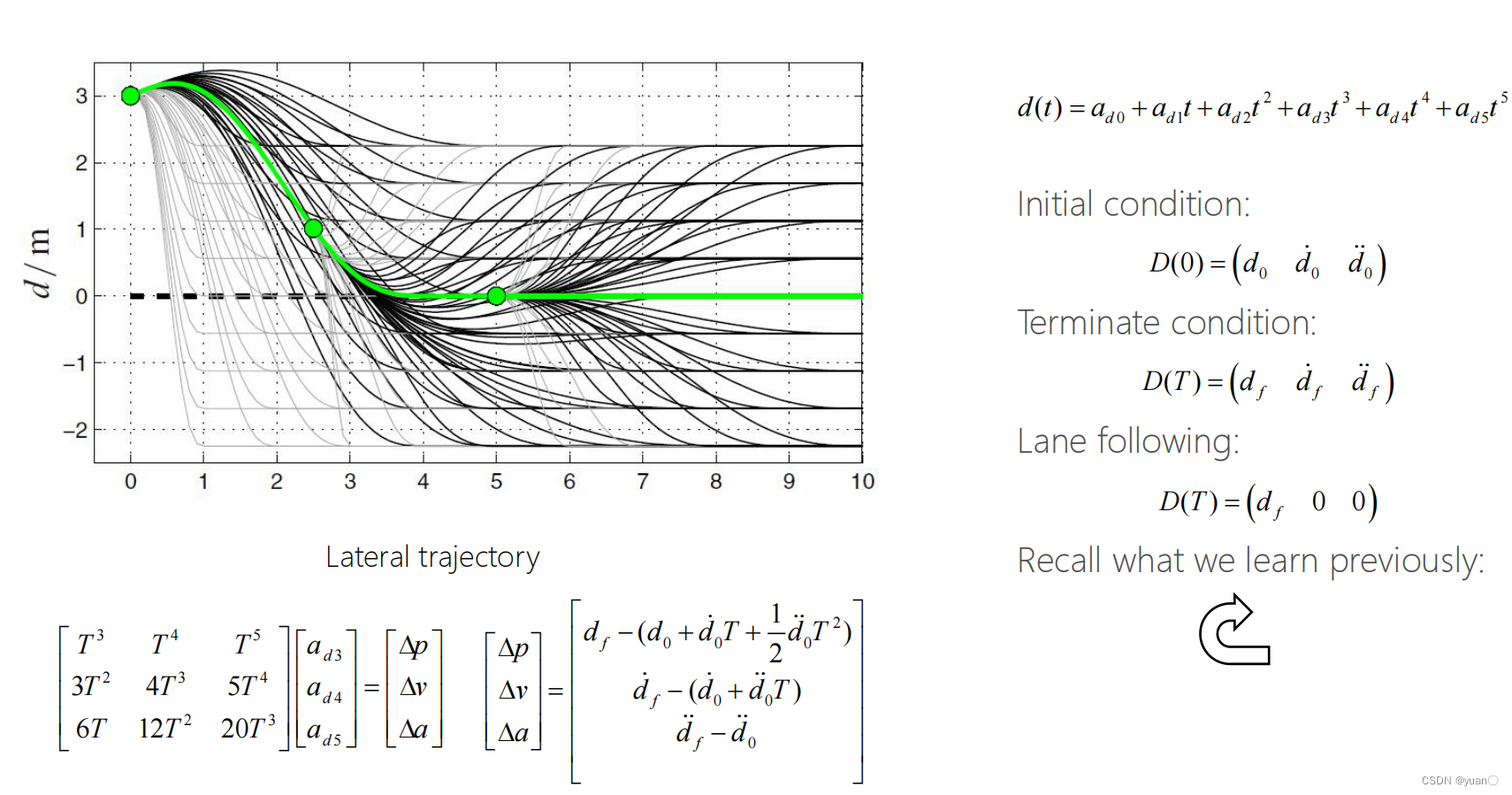
PS1:横纵向解耦
PS2:构造横纵方向上的五次多项式，确定起始条件和终止条件（车道线跟踪时的终止条件要注意）

论文：Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame, Moritz Werling, Julius Ziegler, Sören Kammel, and Sebastian Thrun
论文：Optimal trajectories for time-critical street scenarios using discretized terminal manifolds, Moritz Werling, Sören Kammel, Julius Ziegler and Lutz Gröll

Hybrid A*

论文：Practical Search Techniques in Path Planning for Autonomous Driving, Dmitri Dolgov, Sebastian Thrun Path Planning for
论文：Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments, Dmitri Dolgov, Sebastian Thrun

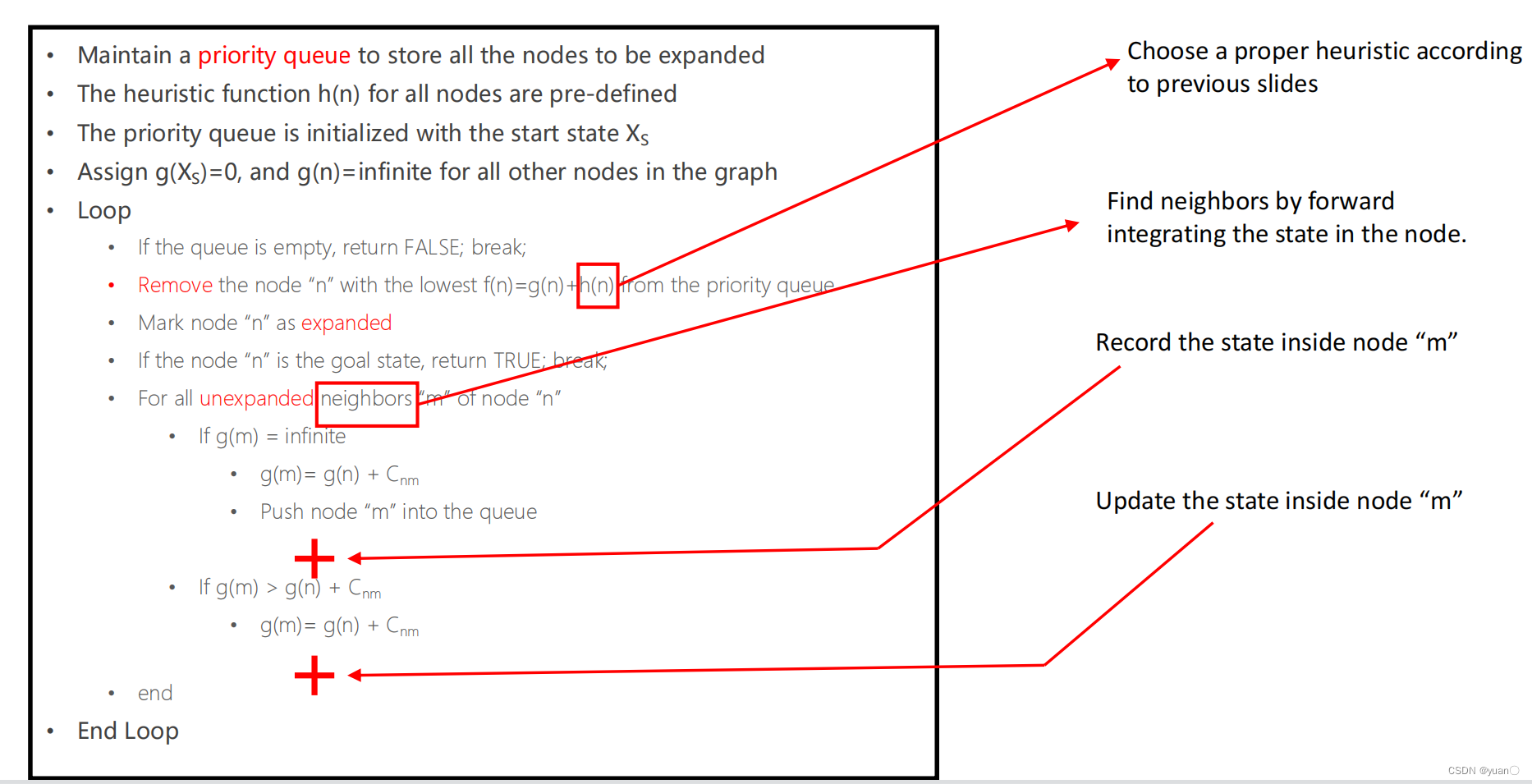
稠密的lattice graph构建会花费大量的时间、占据大量计算资源，需要对其进行剪枝(prune)。hybrid Astar 采用了lattice和栅格地图结合的方式进行剪枝，保证每一个栅格内只有状态点。

hybrid Astar 和Astar的伪代码有以下几点不同：

1. 启发函数不同。
2. 扩展节点的方式不同。hybrid Astar通过对state的推算进行扩展。
3. 要记录节点的状态state
4. 要对节点的state进行更新
   

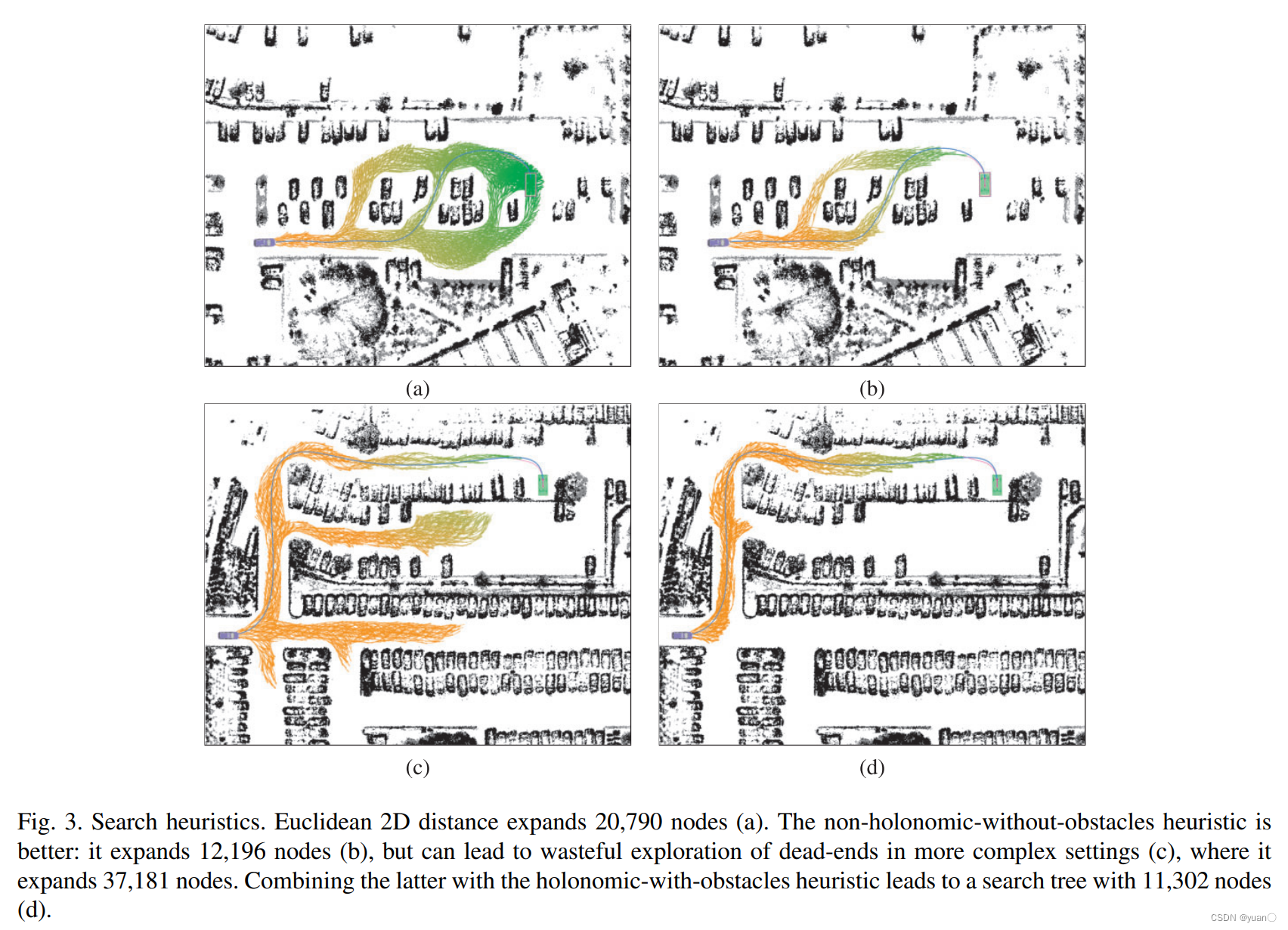
启发函数的设计

non-holonomic-without-obstacles + holonomic-with-obstacles
结合考虑动力学不考虑障碍物的估计方法与考虑障碍物不考虑动力学的估计方法。

其他技巧

Analytic Expansions: One shot heuristic Add a state-driven bias towards the searching process

每个N个节点，对扩展的节点直接计算到终点的曲线，若符合动力学约束且无障碍，则直接结束规划。对于N的设计，可以与终点的距离成反比。

另：
Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight, Boyu Zhou, Fei Gao
https://github.com/HKUST-Aerial-Robotics/Fast-Planner

Kinodynamic RRT*

RRT*具体细节回顾上一讲【移动机器人运动规划】02 —— 基于采样的规划算法

如何采样

不仅仅要对位置（$x,y,z$）进行采样，需要对整个状态空间进行采样，包括($p,v$)等状态变量。

如何进行最优控制的连接

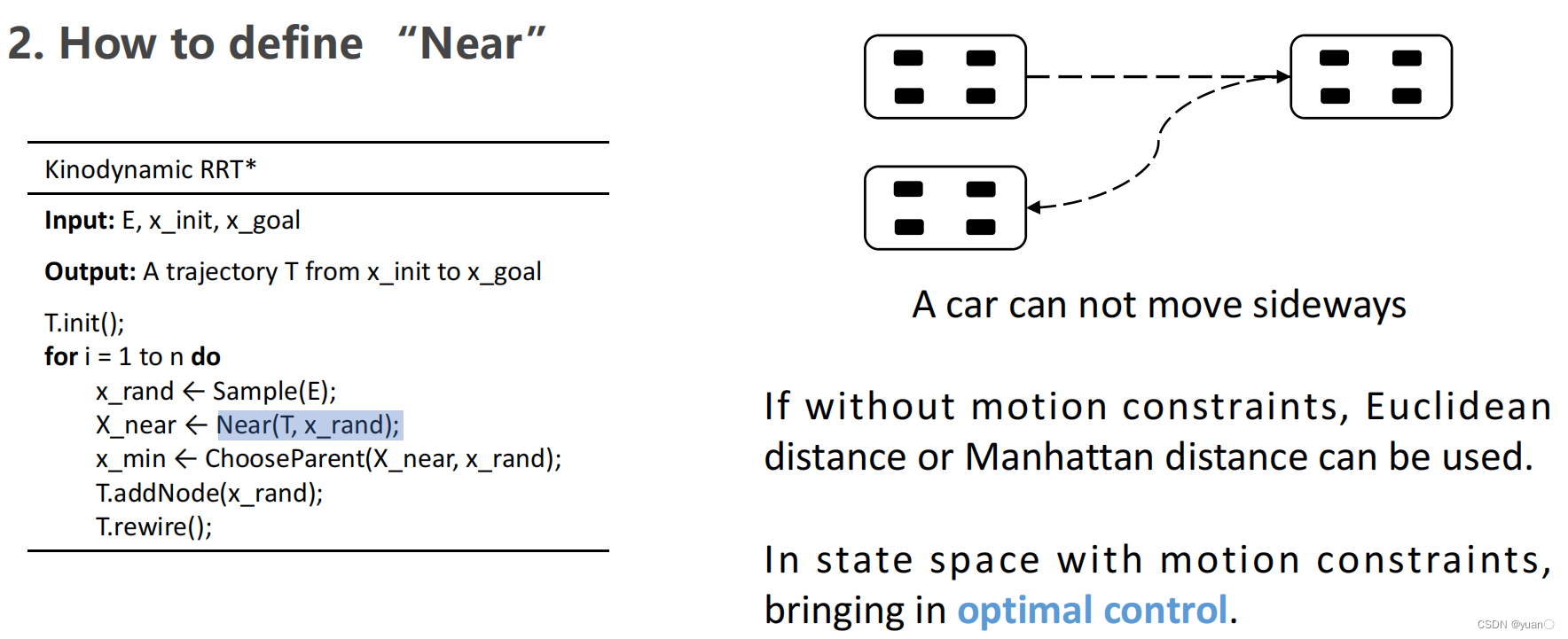
目标函数是（时间+控制量$u^2$），$R$是权重。

用controllability Gramian的方式去求解lyapunov equation，求解出最优控制为$u^{\ast }(t)$

$c[\tau ]$为关于时间和控制量$u$的代价函数

chooseparent 查找的范围不仅仅是以欧式距离作为指标，而是以最优控制的cost最为指标

高维kdtree查询

参考文献

[1] Search-based Motion Planning for Quadrotors using Linear Quadratic Minimum Time Control，Sikang Liu, Nikolay Atanasov, Kartik Mohta, and Vijay Kumar
[2] Generating Near Minimal Spanning Control Sets for Constrained Motion Planning in Discrete State Spaces，Mihail Pivtoraiko and Alonzo Kelly
[3] Optimal Rough Terrain Trajectory Generation for Wheeled Mobile Robots, Thomas M. Howard Alonzo Kelly
[4] State Space Sampling of Feasible Motions for High-Performance Mobile Robot Navigation in Complex Environments, Thomas M. Howard, Colin J. Green, and Alonzo Kelly
[5] A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation, Mark W. Mueller, Markus Hehn, and Raffaello D’Andrea Dynamic Programming and Optimal Control, D. P. Bertsekas
[6] 庞特里亚金最小值原理解最优控制问题
[7] Maximum Likelihood Path Planning for Fast Aerial Maneuvers and Collision Avoidance Ji Zhang, Chen Hu, Rushat Gupta Chadha, and Sanjiv Singh
[8] Planning Long Dynamically Feasible Maneuvers for Autonomous Vehicles, Maxim Likhachev, Dave Ferguson
[9] Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments, Dmitri Dolgov, Sebastian Thrun, Michael Montemerlo, James Diebel
[10] Optimal trajectories for time-critical street scenarios using discretized terminal manifolds, Moritz Werling, Sören Kammel, Julius Ziegler and Lutz Gröll
[11] Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame, Moritz Werling, Julius Ziegler, Sören Kammel, and Sebastian Thrun
[12] Practical Search Techniques in Path Planning for Autonomous Driving, Dmitri Dolgov, Sebastian Thrun Path Planning for
[13] F. Lewis, V. Syrmos. Optimal Control. John Wiley & Sons