红黑树
- 一、什么是红黑树?
- 1.1 AVL树
- 1.2 红黑树
- 二、红黑树的特点
- 三、红黑树的insert、delete
- 3.1 insert
- 3.1.1 父节点为空
- 3.1.2 父节点为Black节点
- 3.1.3 父节点为Red节点
- 3.1.3.1 叔叔节点为Red节点
- 3.1.3.2 叔叔节点为Black节点
- 3.2 delete
- 3.2.1 删除节点有两个子节点
- 3.2.2 删除节点只有一个子节点
- 3.2.3 删除节点无子节点
- 3.2.3.1 删除节点为红色节点
- 3.2.3.2 删除节点为黑色节点
- 1. 兄弟节点为Red
- 2. 兄弟节点为黑色节点
一、什么是红黑树?
在谈及红黑树前,首先我们先了解一下什么AVL(平衡二叉树)树。
1.1 AVL树
AVL树,也叫平衡二叉树,具有以下特点:
- 本身就为一颗 二叉搜索树。
- 每个结点的左右子树的高度之差的绝对值最多为 1。
- 每个节点都是 AVL 树。
- 可以为空。
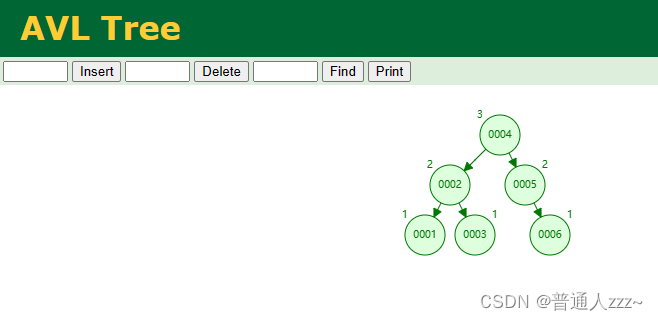
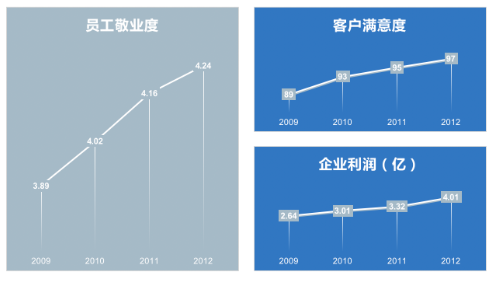
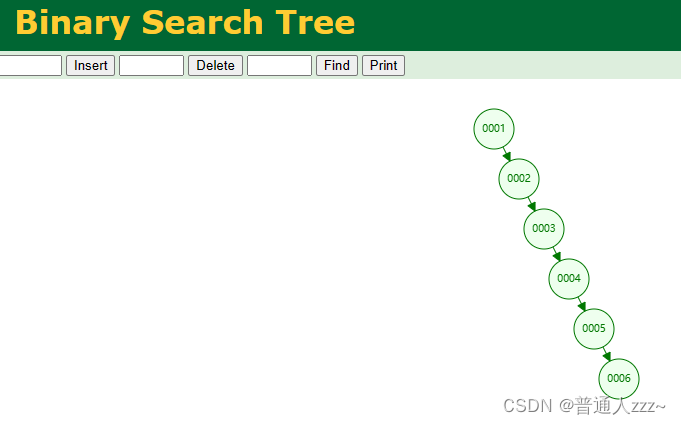
AVL树相比于二叉搜索树,具有更高的查询效率,因为在一些极端场景下,二叉搜索树(Binary Search Tree),会蜕化为链表(如下图),使得搜索的时间复杂度为 O(N),AVL树时间复杂度严格为 O(log2N)。
因为具有以上特点,所以在进行插入、删除节点时,需通过多次旋转节点来满足上述特点,因此,AVL树在查找上效率较高,但是在插入、删除上,效率较低。
因此,一些大牛为满足效率上的提升,对AVL树进行“升级”,红黑树概念由此产生,具体如下:
1.2 红黑树
红黑树是一种特殊的AVL树,通过在插入、删除时多次旋转节点来保持二叉查找树的平衡,从而获得较高的查找性能(O(log2N))。但是红黑树又是一种非严格意义上的AVL树,它的左右子树高差有可能大于 1,但对之进行平衡的代价较低, 使得其性能要远远强于 AVL树。所以在多数计算机语言中,通用使用红黑树,来替代AVL树,进行高效查找、删除、插入。
二、红黑树的特点
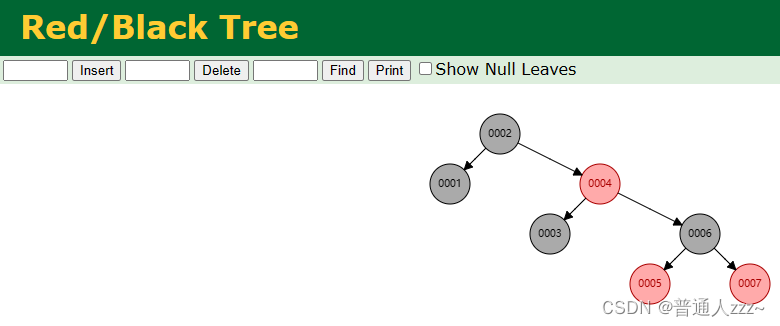
红黑树是一种自平衡的AVL树,其特点如下:
- 可以为空树。
- 如果不为空树,其根节点必须为黑色节点。
- 每个节点的左子节点值都小于父节点,每个节点右子节点都大于父节点值。
- 任何相邻的节点都不能同时为红色节点。
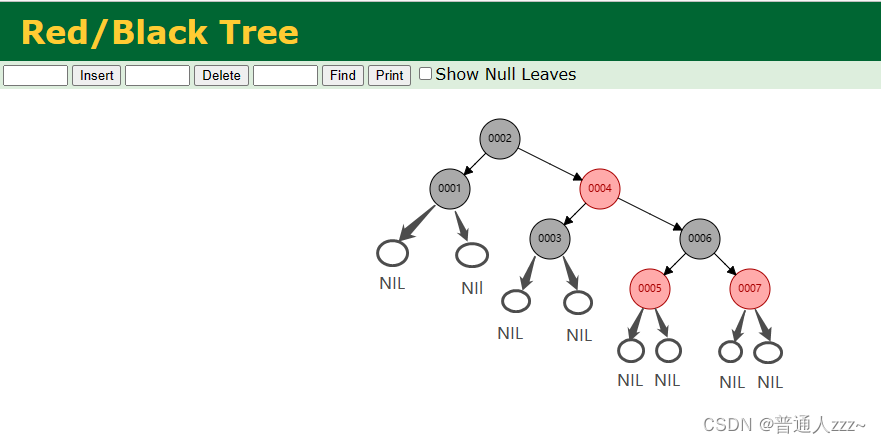
- 每个叶子节点都具有黑色的空节点(NIL),如下图,叶子节点不存储数据,只为满足特点6。
- 每个节点,从该节点到所有可达叶子节点的所有路径,其包含的黑色节点数目都相同,如节点 0004到所有叶子节点都有两个黑色节点。
- 节点的插入,都为红色节点,通过旋转和着色来满足红黑树的其他特征。
三、红黑树的insert、delete
3.1 insert
红黑树的节点insert,初始颜色都为Red,通过旋转和着色来满足红黑树的其他特征。节点的insert又可以分为以下几种情况:
- 插入的节点,其父节点为空;
- 插入的节点,其父节点为Black节点;
- 插入的节点,其父节点为Red节点;
3.1 叔叔节点为Black节点;
3.2 叔叔节点为Red节点;
具体详情下面一一分析。
3.1.1 父节点为空
父节点为空,既当前Tree 为空,直接插入。
通过红黑树的特点可知,根节点为Black节点,所以需要重新着色。
3.1.2 父节点为Black节点
父节点为Black节点,插入节点为Red节点,由红黑树特点可知,直接插入当前节点即可满足其所有特点。
3.1.3 父节点为Red节点
当父节点为Red节点时,不满足红黑树特点:任何相邻的节点都不能同时为红色节点,所以需要旋转、着色。
3.1.3.1 叔叔节点为Red节点
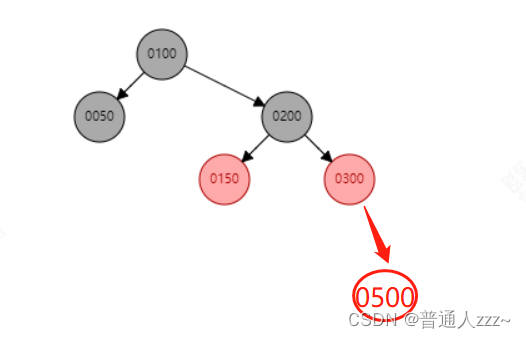
如上图,当插入节点父节点、叔叔节点均为Red节点时,为满足特点:任何相邻的节点都不能同时为红色节点;每个节点,从该节点到所有可达叶子节点的所有路径,其包含的黑色节点数目都相同。所以,需要重新进行着色,将父节点、叔叔节点颜色修改为Black,爷爷节点修改为Red节点。

这就完了么???NO!NO!NO!
试想一下,如果祖父节点恰好为Red节点,是否相邻节点又都为红色节点,如下图所示:
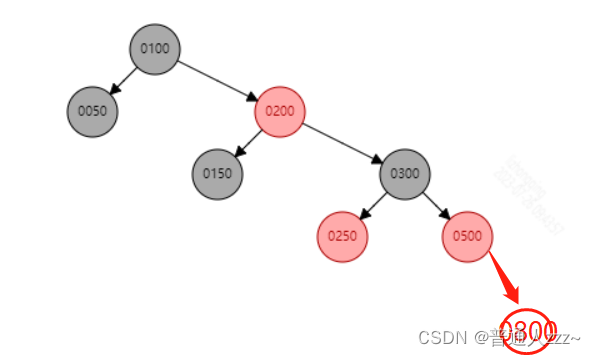
插入一个新节点 800,满足父节点、叔叔节点均为红色,则先将父节点、叔叔节点颜色修改为Black,爷爷节点修改为Red节点。如下:
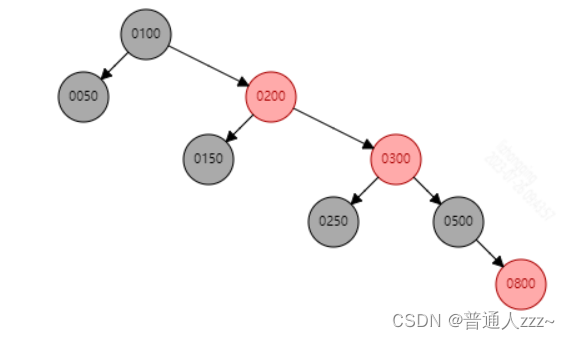
这时,节点 0200 与 节点 0300 都为Red节点,且 0300 的兄弟节点一定为Black节点(任何相邻的两个节点不能同时为Red节点),所以将 0300 节点当做新插入的节点,情况就变为了 3.1.3.2 叔叔节点为Black节点,具体操作步骤下面详细分析。
3.1.3.2 叔叔节点为Black节点
当父节点为Red节点、叔叔节点为Black节点,如下图:
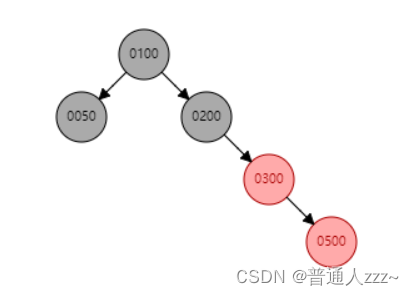
插入节点 0500,其父节点为Red节点,叔叔节点为NIL黑色节点,需根据具体情况来进行旋转、着色,如下:
condition 1(左左):父节点为左子节点,插入节点为左子节点。
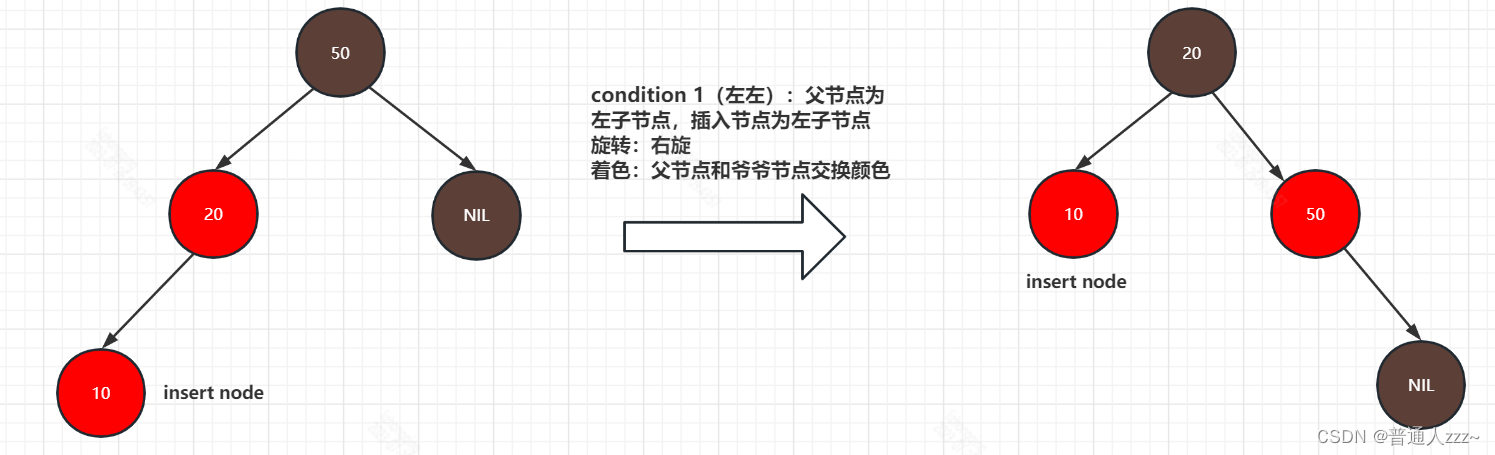
condition 2(左右):父节点为左子节点,插入节点为右子节点。

condition 3(右右):父节点为右子节点,插入节点为右子节点。
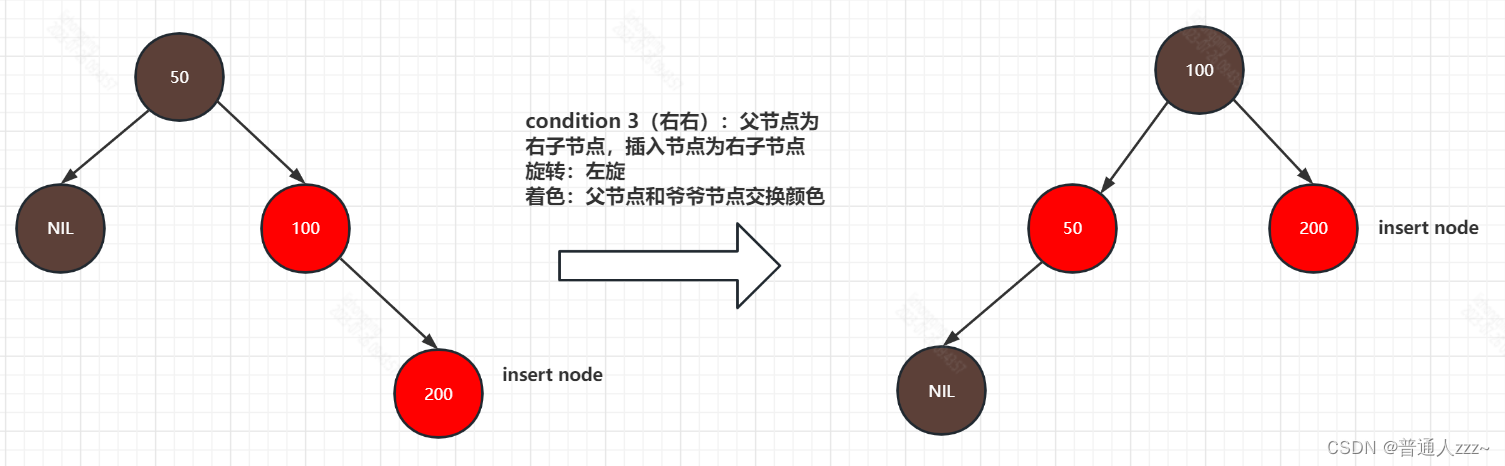
condition 4(右左):父节点为右子节点,插入节点为左子节点。

3.2 delete
红黑树节点的删除与二叉搜索树(AVL树)一样,也分为三种情况,如下:
- 删除节点无子节点;
- 删除节点只有一个子节点;
- 删除节点有两个子节点;
红黑树删除,采用以繁化简进行处理,**对于非叶子节点的删除,最终都转化为对叶子节点的删除。**通过这个思想,下面对以上情况进行详细分析。
3.2.1 删除节点有两个子节点
在了解中间节点的删除前,我们先了解两个概念:
-
前驱节点: 在中序遍历中,一个节点的前驱结点,先找到该节点的左孩子节点,再找左孩子节点的最后一个右孩子节点。向左走一步,然后向右走到头。最后一个右孩子节点即为前驱节点。
-
后继节点: 在中序遍历中,一个节点的后继结点,先找到该节点的右孩子节点,再找右孩子节点的最后一个左孩子节点。向右走一步,然后向左走到头。最后一个左孩子节点即为后继结点。
采用以繁化简进行处理,对于非叶子节点的删除,最终都转化为对叶子节点的删除。
- 当删除节点为中间节点是,寻找当前节点的前驱节点,交换前驱节点与删除节点的值,然后直接删除前驱节点;
- 如果不存在前驱节点,则寻找当前接的后继节点,交换后继节点与删除节点的值,直接删除后继节点;
通过上述操作,将复杂的中间节点删除,转换为叶子节点删除,叶子节点的删除,参照步骤 3.2.2 删除节点只有一个子节点、3.2.3 删除节点无子节点。
3.2.2 删除节点只有一个子节点
将删除节点的父节点指向当前节点的子节点,直接删除,并交换删除节点、子节点颜色,保持颜色平衡,如下:
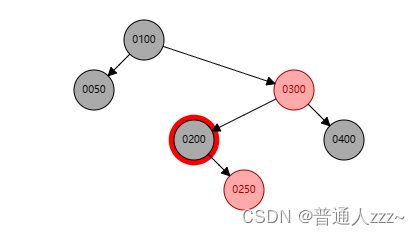
- 将删除节点的父节点指向当前节点的子节点
- 直接删除当前节点
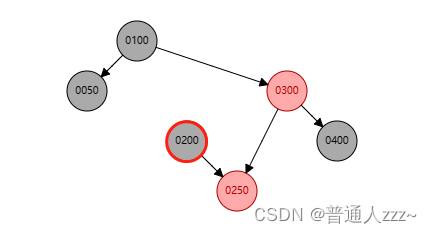
- 交换删除节点、子节点颜色
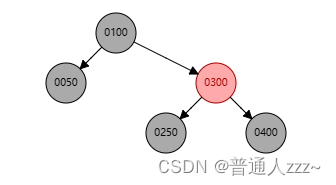
3.2.3 删除节点无子节点
3.2.3.1 删除节点为红色节点
当前模式最为简单,红色叶子节点删除,不影响红黑树平衡,所以可以直接删除即可。
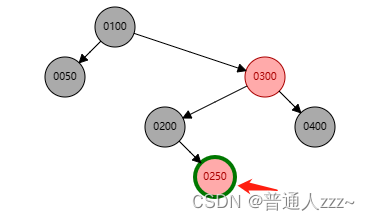
- 删除红色节点 250:直接删除
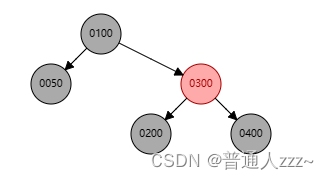
3.2.3.2 删除节点为黑色节点
当删除节点为黑色节点时,由于影响到红黑树的特点(每个节点,从该节点到所有可达叶子节点的所有路径,其包含的黑色节点数目都相同,这种特定称为黑高相同),所以需要进行旋转、着色来修复红黑树。
可分为以下几种情况。
1. 兄弟节点为Red
- 1 父节点为红色节点:不存在当前情况,无需考虑。
- 2 父节点为黑色节点;
- 2.1 兄弟节点无子节点:不存在当前情况,需保持黑高相同
- 2.2 兄弟节点存在一个子节点:不存在当前情况,需保持黑高相同
- 2.3 兄弟节点存在两个子节点:分析可知,两个子节点均为红色节点
最终,当兄弟节点为Red节点时,父节点一定为Black节点,且兄弟节点一定存在两个子节点,两个子节点均为红色,如下:
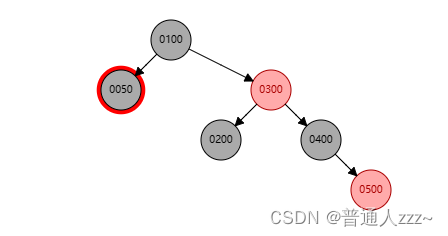
(图1)
删除步骤如下:
- 直接删除节点;
- 将兄弟节点设置为Black;
- 如果删除节点为左子节点
- 则将兄弟节点左子节点设置为红色;
- 对父节点进行左旋;
- 如果兄弟节点的左子节点(BLeft)存在子节点;
- 存在左子节点:对BLeft进行右旋,然后对BLeft的父节点进行左旋,设置BRight左子节点为Black。
- 存在右子节点:对BLeft的父节点进行左旋,交换BLeft与BLeft右子节点的颜色。
- 存在左右子节点:对BLeft的父节点进行左旋,交换BLeft与BLeft右子节点的颜色。
- 如果删除节点为右子节点
- 则将兄弟节点右子节点设置为红色;
- 对父节点进行右旋;
- 如果兄弟节点的右子节点(BRight)存在子节点;
- 存在左子节点:对BRight的父节点进行右旋,交换BRight与BRight左子节点的颜色。
- 存在右子节点:对BRight进行左旋,然后对BRight的父节点进行右旋,设置BRight右子节点为Black。
- 存在左右子节点:对BRight的父节点进行右旋,交换BRight与BRight左子节点的颜色。
删除图1中的Black节点 0050,通过以上步骤,最终红黑树如图二所示。
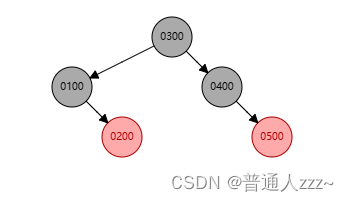
(图二)
2. 兄弟节点为黑色节点
注意:分析可知,当前节点为Black节点,兄弟节点也为Black节点,则如果兄弟节点存在子节点,子节点颜色一定为Red节点。
- 1 父节点为红色节点:
- 1.1 兄弟节点无子节点:直接交换父节点、兄弟节点颜色;
- 1.2 兄弟节点存在一个子节点;
- 1.2.1 存在左子节点:① 删除节点为左子节点:将兄弟节点右旋,然后将父节点左旋,最后把兄弟节点左子节点颜色修改为Black,并修改兄弟节点颜色为Red;② 删除节点为右子节点:将父节点右旋;
- 1.2.2 存在右子节点:① 删除节点为左子节点:将父节点左旋;② 删除节点为右子节点:将兄弟节点左旋,然后将父节点右旋,最后把兄弟节点右子节点颜色修改为Black,并修改兄弟节点颜色为Red;
- 1.3 兄弟节点存在两个子节点;
- 1.3.1 删除节点为左子节点:将父节点左旋,然后将兄弟节点右子节点修改为Black;
- 1.3.2 删除节点为右子节点:将父节点右旋,右旋后,会导致两个节点连续为红色,把之前兄弟节点的右子节点当做插入的节点,走新增节点3.1.3父节点为Red节点、3.1.3.1叔叔节点为Red节点;
- 2 父节点为黑色节点;
- 2.1 兄弟节点无子节点;
- 2.1.1 不存在祖父节点:直接将兄弟节点颜色修改为红色;
- 2.1.2 存在祖父节点:直接将兄弟节点颜色修改为红色;以父节点作为条件判断,将父节点赋值个当前节点,递归处理,判断其父节点、兄弟节点颜色。
- 2.2 兄弟节点存在一个子节点;
- 2.2.1 存在左子节点:① 删除节点为左子节点:将兄弟节点右旋,然后将父节点左旋,最后把兄弟节点左子节点颜色修改为Black;② 删除节点为右子节点:将父节点右旋,然后把兄弟节点左子节点颜色修改为Black;
- 2.2.2 存在右子节点:① 删除节点为左子节点:将父节点左旋,然后把兄弟节点右子节点颜色修改为Black;② 删除节点为右子节点:将兄弟节点左旋,然后将父节点右旋,最后把兄弟节点右子节点颜色修改为Black;
- 2.3 兄弟节点存在两个子节点;
- 2.3.1 删除节点为左子节点:将父节点左旋,然后将兄弟节点右子节点修改为Black;
- 2.3.2 删除节点为右子节点:将父节点右旋,然后将兄弟节点左子节点修改为Black;
- 2.1 兄弟节点无子节点;