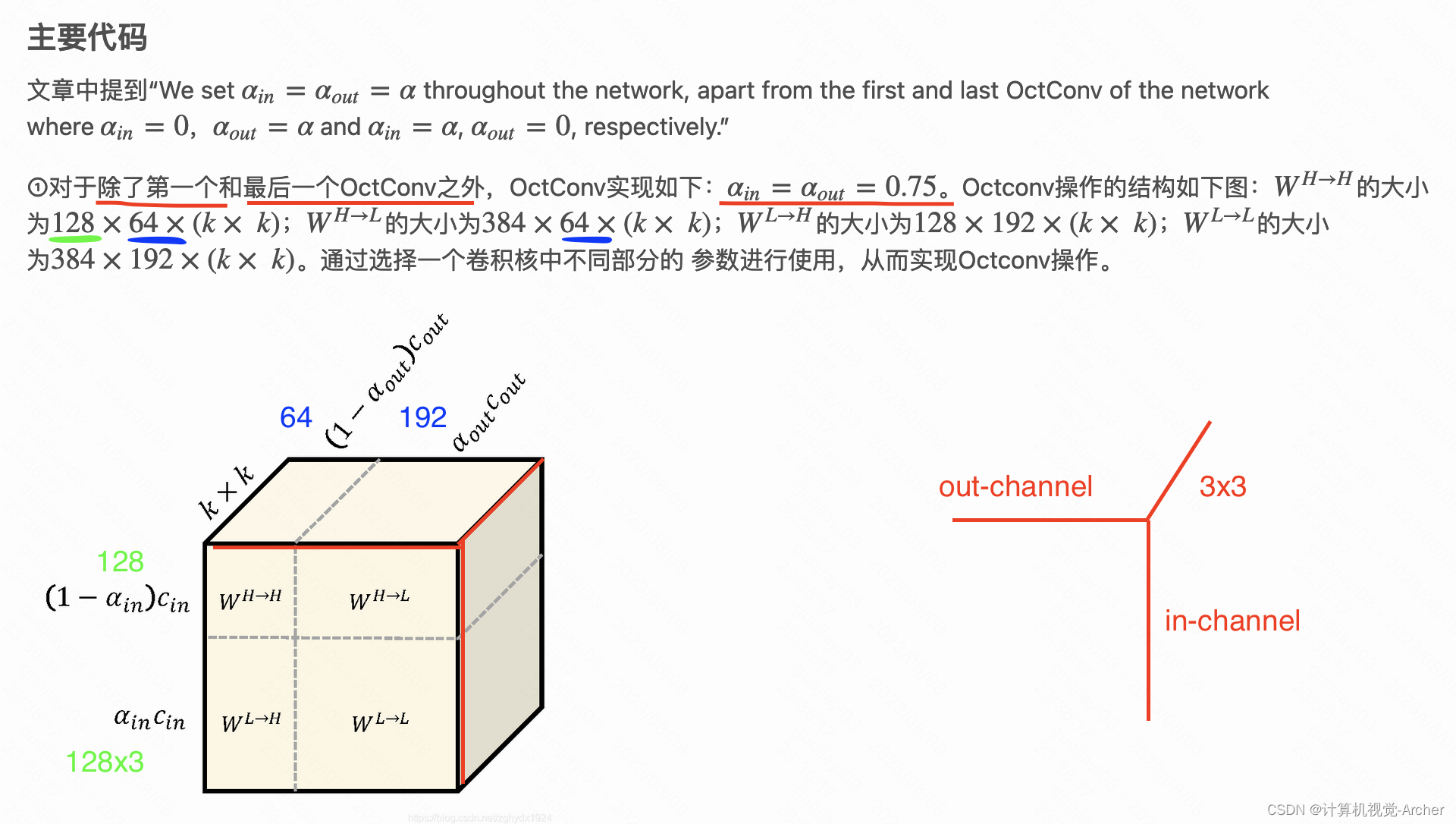
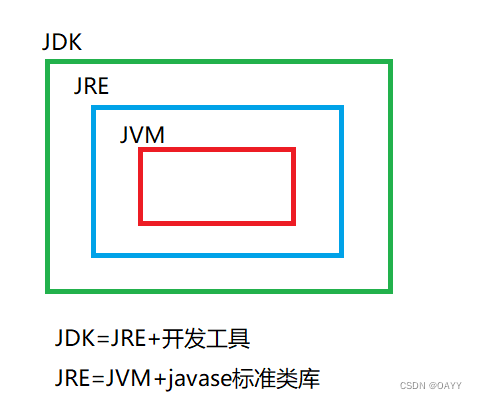
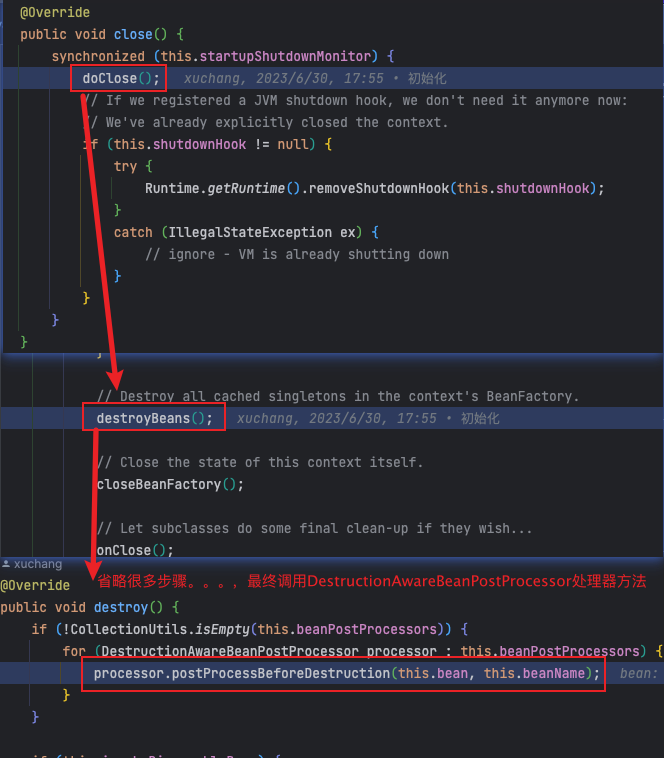
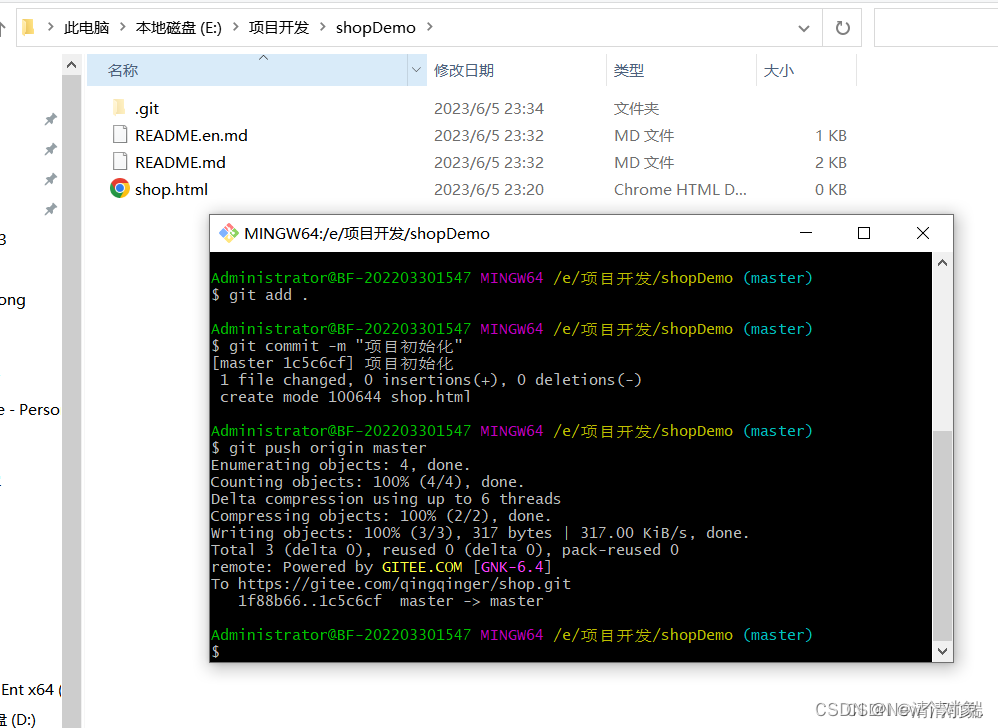
一、说明
在本系列中,我们将学习如何仅使用普通和现代C++编写必须知道的深度学习算法,例如卷积、反向传播、激活函数、优化器、深度神经网络等。
在这个故事中,我们将通过引入梯度下降算法来介绍数据中 2D 卷积核的拟合。我们将使用卷积和上一个故事中引入的成本函数概念,将所有内容编码为现代C++和特征。

这个故事是:C++的梯度下降,查看其他故事:
0 — 现代C++深度学习编程基础
1 — 在C++中编码 2D 卷积
2 — 使用 Lambda 的成本函数
4 — 激活函数
...更多内容即将推出。
二、函数逼近作为优化问题
如果你读过我们之前的演讲,你已经知道,在机器学习中,我们大部分时间都在关注使用数据来寻找函数近似值。
通常,我们通过找到最小化成本值的系数来获得函数近似。因此,我们的近似问题被转换为优化问题,我们试图最小化成本函数的值。
三、成本函数和梯度下降
成本函数计算使用函数 H(X) 近似目标函数 F(X) 的开销。例如,如果 H(X) 是输入 X 和核 k 之间的卷积,则 MSE 成本函数由下式给出:
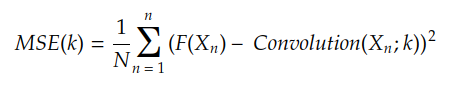
我们通常做 Yn = F(Xn),结果是:
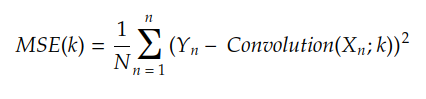
MSE是均方误差,是上一个故事中介绍的成本函数
因此,我们的目标是找到最小化MSE(k)的内核值km。找到 km 的最基本(但最强大)的算法是梯度下降。
梯度下降使用成本函数梯度来查找最小成本。为了理解什么是梯度,让我们谈谈成本表面。
四、绘制成本曲面
为了更容易理解,让我们暂时假设内核仅由两个系数组成。如果我们为每个可能的组合绘制 MSE(k) 的值,我们最终会得到这样的表面:k[k00, k01][k00, k01]

在每个点上,曲面与0k₀₀轴有一个倾角,与0k₀₁轴有另一个倾角:(k00, k01, MSE(k00, k01))
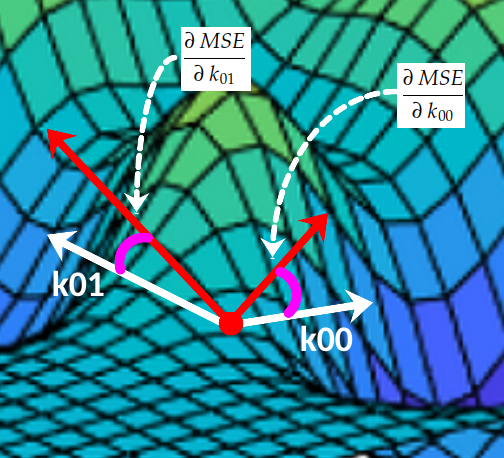
偏导数
这两个斜率分别是 MSE 曲线相对于轴 O k₀₀ 和 Ok₀₁ 的偏导数。在微积分中,我们非常使用符号∂来表示偏导数:
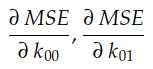
这两个偏导数共同构成了MSE相对于轴O k₀₀和Ok₀₁的梯度。此梯度用于驱动梯度下降算法的执行,如下所示:
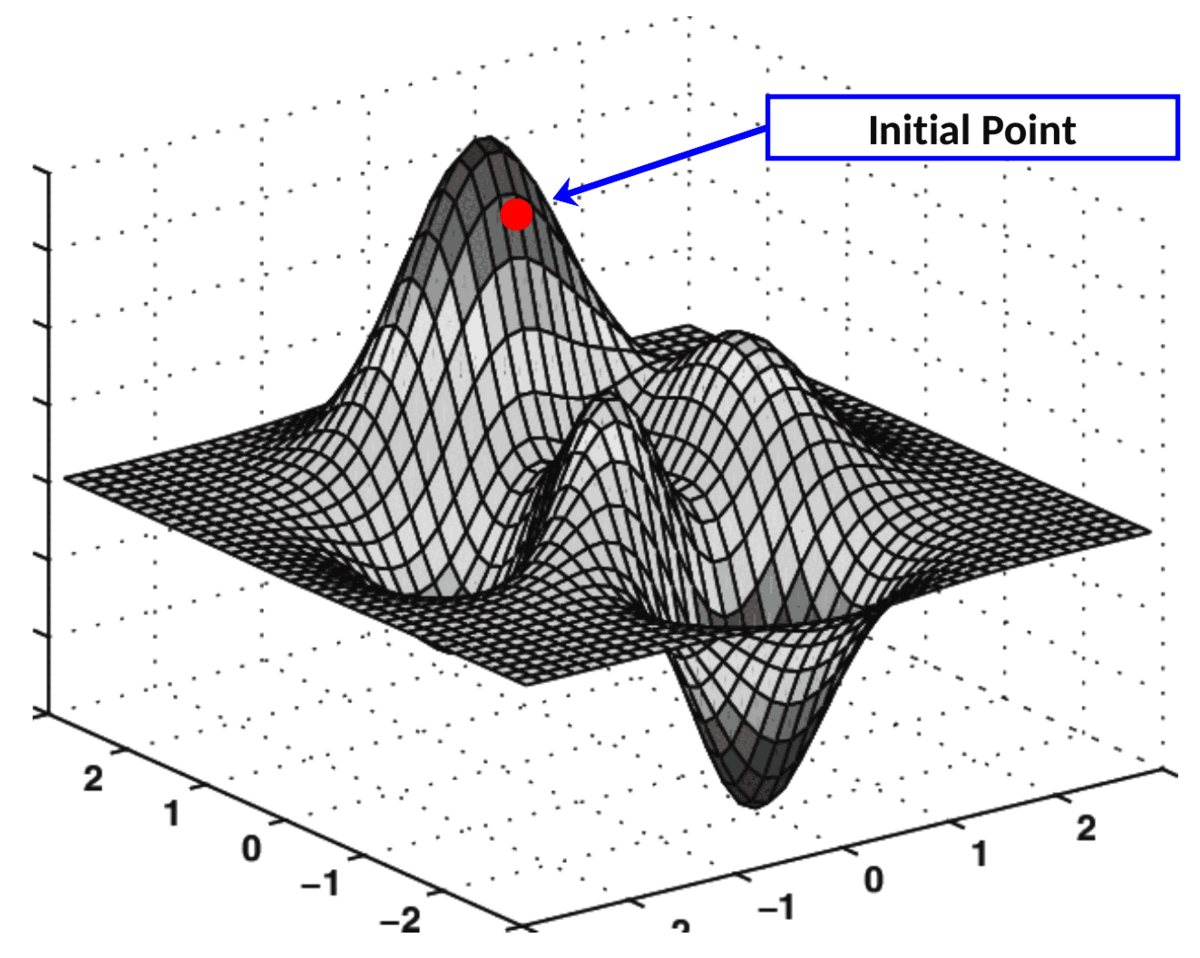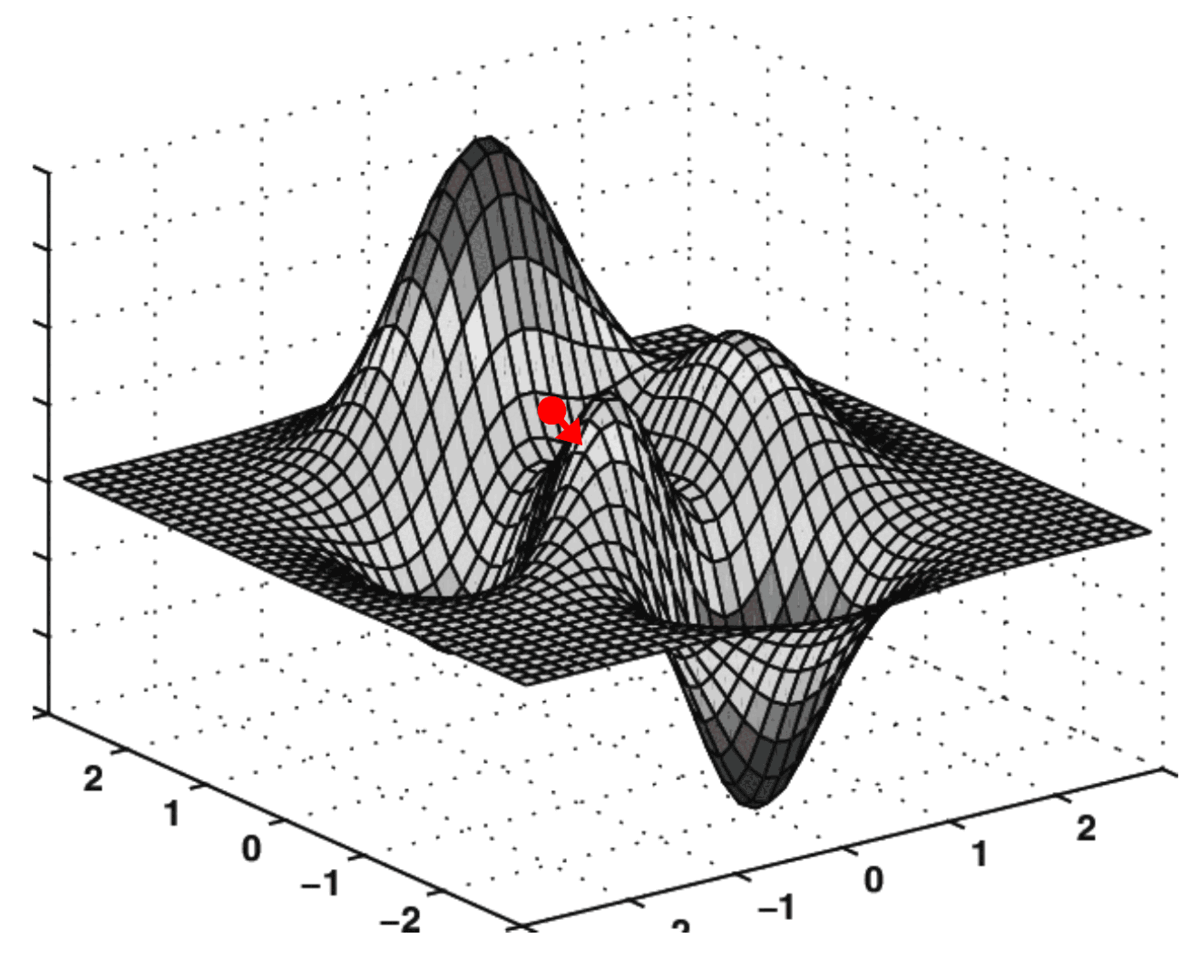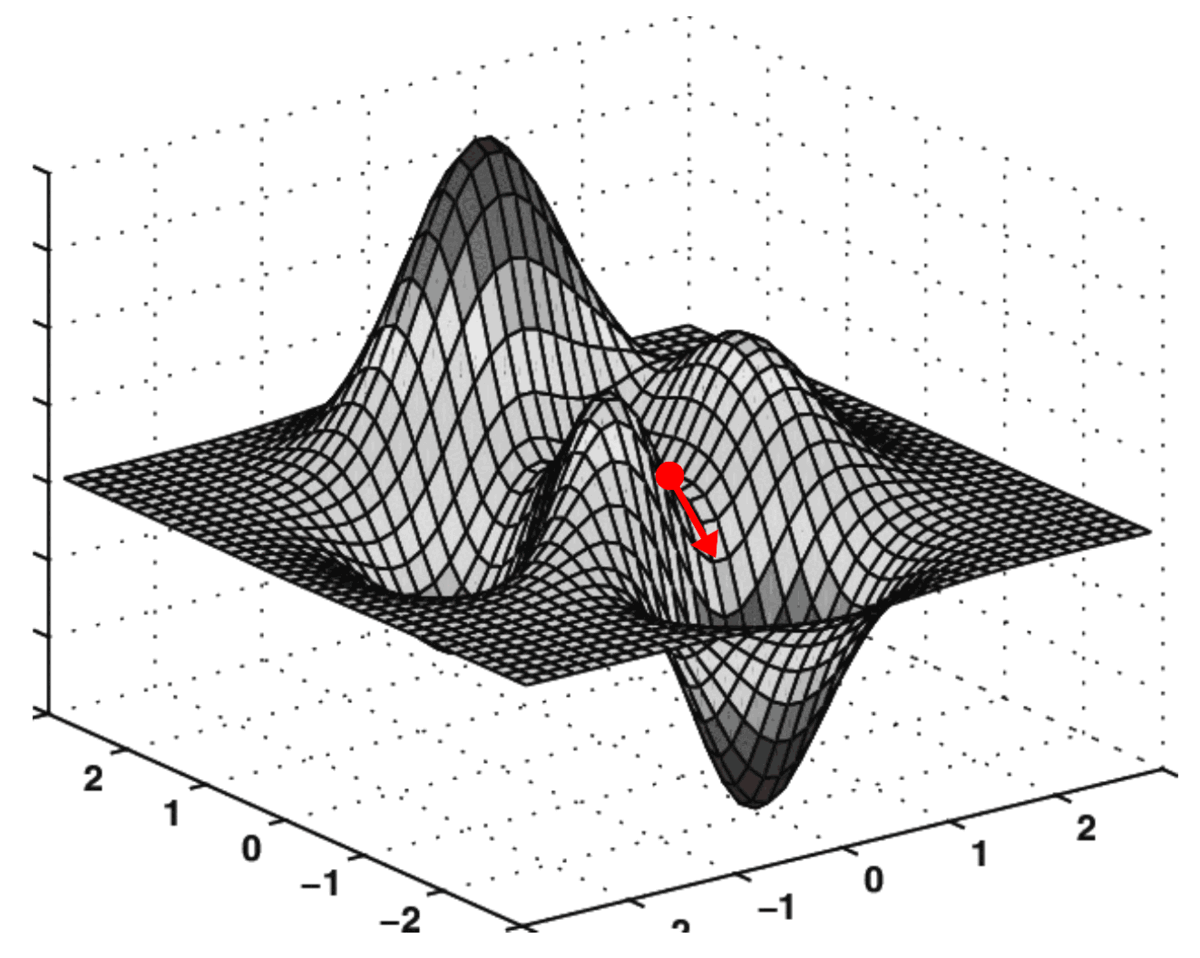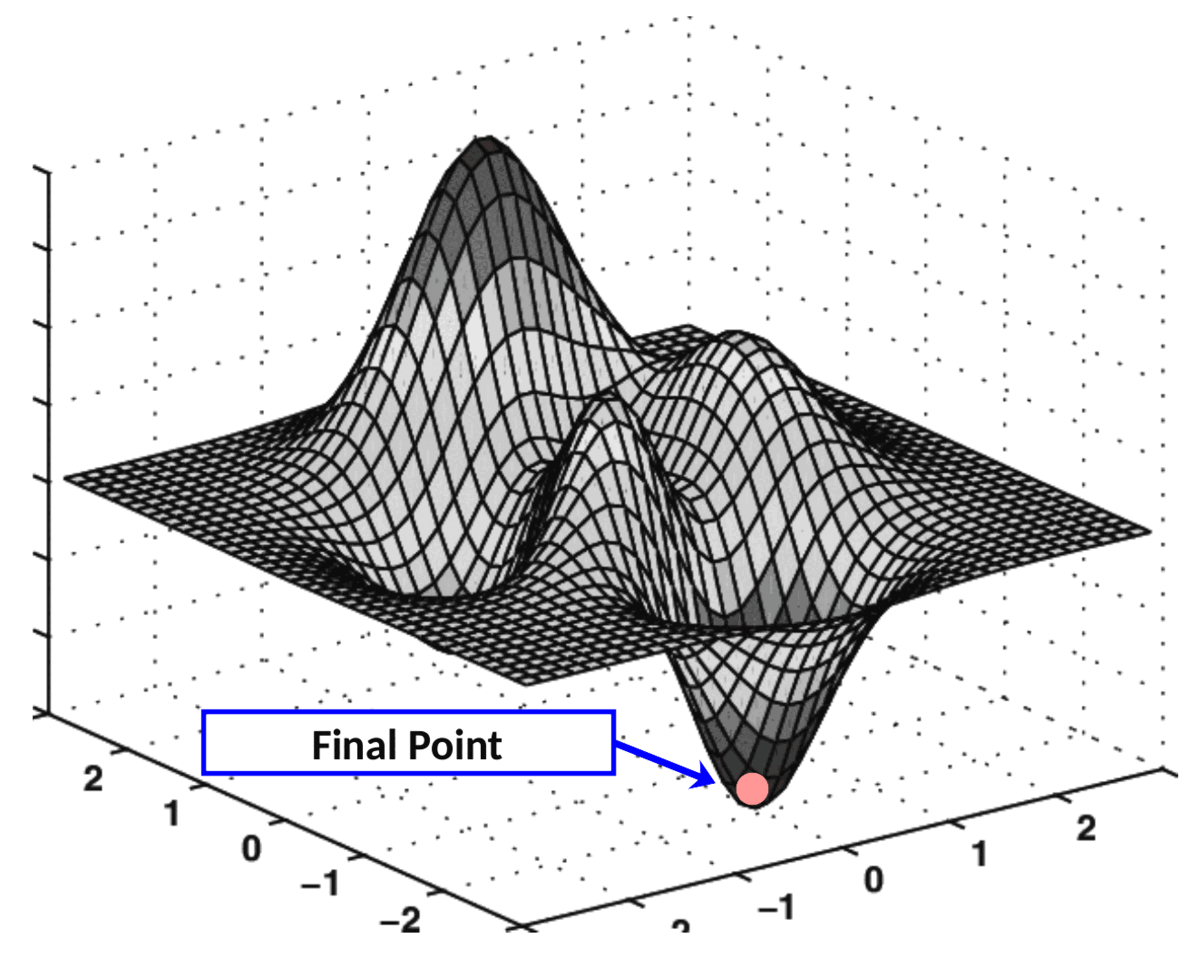
梯度下降的实际应用
在成本表面上执行此“导航”的算法称为梯度下降。
五、梯度下降
梯度下降伪代码描述如下:
gradient_descent:
initialize k, learning_rate, epoch = 1
repeat
k = k - learning_rate x ∇Cost(k)
until epoch <= max_epoch
return klearning_rate x ∇Cost(k) 的值通常称为权重更新。我们可以通过以下方式恢复梯度下降的行为:
for each iteration:
calculate the weight update
subtract it from the parameter k顾名思义,Cost(k) 是配置 k 的成本函数。梯度下降的目的是找到成本(k)最小的k值。
learning_rate通常是像 0.1、0.01、0.001 左右这样的标量。此值控制优化过程中的步长。
该算法循环 max_epoch 次。有时,我们会更早地停止算法,即,即使纪元< max_epoch,在 Cost(k) 太小的情况下。
我们通常用超参数的名称来指代learning_rate和max_epoch等参数。
要实现梯度下降,我们需要知道的最后一件事是如何计算 C(k) 的梯度。幸运的是,在成本函数为 MSE 的情况下,如前所述,查找 ∇Cost(k) 非常简单。
六、查找 MSE 梯度
到目前为止,我们已经看到梯度的分量是每个轴 0kij 的成本面的斜率。我们还看到,MSE(k) 相对于每个 i 个、核 k 的系数 j-的梯度由下式给出:
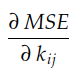
让我们记住,MSE(k) 由下式给出:
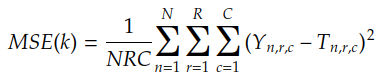
其中n是每对的索引(Yn,Tn),r&c是输出矩阵系数的索引:
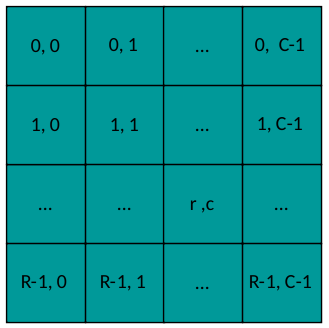
输出布局
使用链式规则和线性组合规则,我们可以通过以下方式找到MSE梯度:
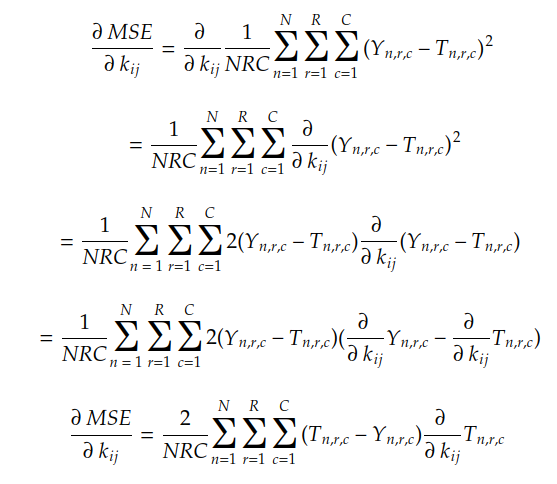
由于 N、R、C、Yn 和 T n 的值是已知的,我们需要计算的只是 Tn 中每个系数相对于系数 kij 的偏导数。在带有填充 P 的卷积的情况下,此导数由下式给出:
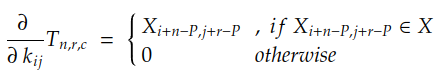
如果我们展开 r 和 c 的总和,我们可以发现梯度由下式给出:
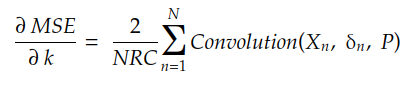
其中 δn 是矩阵:
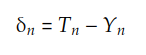
以下代码实现此操作:
auto gradient = [](const std::vector<Matrix> &xs, std::vector<Matrix> &ys, std::vector<Matrix> &ts, const int padding)
{
const int N = xs.size();
const int R = xs[0].rows();
const int C = xs[0].cols();
const int result_rows = xs[0].rows() - ys[0].rows() + 2 * padding + 1;
const int result_cols = xs[0].cols() - ys[0].cols() + 2 * padding + 1;
Matrix result = Matrix::Zero(result_rows, result_cols);
for (int n = 0; n < N; ++n) {
const auto &X = xs[n];
const auto &Y = ys[n];
const auto &T = ts[n];
Matrix delta = T - Y;
Matrix update = Convolution2D(X, delta, padding);
result = result + update;
}
result *= 2.0/(R * C);
return result;
};现在我们知道了如何获得梯度,让我们来实现梯度下降算法。
七、编码梯度下降
最后,我们的梯度下降的代码在这里:
auto gradient_descent = [](Matrix &kernel, Dataset &dataset, const double learning_rate, const int MAX_EPOCHS)
{
std::vector<double> losses; losses.reserve(MAX_EPOCHS);
const int padding = kernel.rows() / 2;
const int N = dataset.size();
std::vector<Matrix> xs; xs.reserve(N);
std::vector<Matrix> ys; ys.reserve(N);
std::vector<Matrix> ts; ts.reserve(N);
int epoch = 0;
while (epoch < MAX_EPOCHS)
{
xs.clear(); ys.clear(); ts.clear();
for (auto &instance : dataset) {
const auto & X = instance.first;
const auto & Y = instance.second;
const auto T = Convolution2D(X, kernel, padding);
xs.push_back(X);
ys.push_back(Y);
ts.push_back(T);
}
losses.push_back(MSE(ys, ts));
auto grad = gradient(xs, ys, ts, padding);
auto update = grad * learning_rate;
kernel -= update;
epoch++;
}
return losses;
};This is the base code. We can improve it in several ways, for example:
- using the loss of each instance to update the kernel. This is called Stochastic Gradient Descent (SGD), which is very useful in real-world scenarios;
- grouping instances in batches and updating the kernel after each batch, which is called Minibatch;
- 使用学习率时间表来降低各个时期的学习率;
- 在这一行中,我们可以连接一个优化器,如Momentum、RMSProp或Adam。 我们将在接下来的故事中讨论优化器;
kernel -= update; - 引入验证集或使用某些交叉验证架构;
- 通过矢量化替换嵌套循环以获得性能和 CPU 使用率(如上一个故事所述);
for(auto &instance: dataset) - 添加回调和钩子以更轻松地自定义我们的训练循环。
我们可以暂时忘记这些改进。现在,重点是了解如何使用梯度来更新参数(在我们的例子中是内核)。这是当今机器学习的基本、核心概念,也是推进更高级主题的关键因素。
让我们通过说明性实验将其付诸行动,看看这段代码是如何工作的。
八、实际实验:修复索贝尔边缘探测器
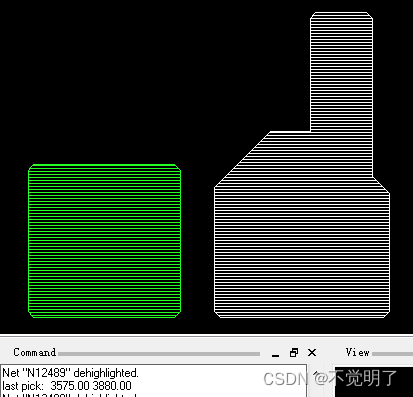
在上一个故事中,我们了解到我们可以应用 Sobel 滤波器 Gx 来检测垂直边缘:
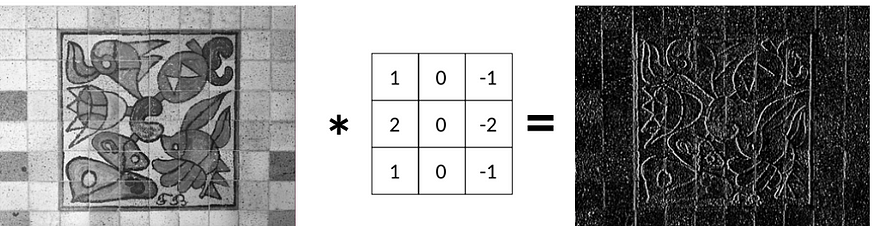
现在,问题是:给定原始图像和边缘图像,我们是否设法恢复了 Sobel 滤镜 Gx?

换句话说,我们可以在给定输入 X 和预期输出 Y 的情况下拟合内核吗?
答案是肯定的,我们将使用梯度下降来做到这一点。
九、加载和准备数据
首先,我们使用OpenCV从文件夹中读取一些图像。我们对它们应用 Gx 过滤器,并将它们成对存储在我们的数据集对象中:
auto load_dataset = [](std::string data_folder, const int padding) {
Dataset dataset;
std::vector<std::string> files;
for (const auto & entry : fs::directory_iterator(data_folder)) {
Mat image = cv::imread(data_folder + entry.path().c_str(), cv::IMREAD_GRAYSCALE);
Mat formatted_image = resize_image(image, 640, 640);
Matrix X;
cv::cv2eigen(formatted_image, X);
X /= 255.;
auto Y = Convolution2D(X, Sobel.Gx, padding);
auto pair = std::make_pair(X, Y);
dataset.push_back(pair);
}
return dataset;
};
auto dataset = load_dataset("../images/");我们使用辅助实用程序 .resize_image 格式化每个输入图像以适合 640x640 网格

如上图所示,将每个图像集中到黑色 640x640 网格中,而无需通过简单地调整图像大小来拉伸图像。resize_image
我们使用 Gx 过滤器为每个图像生成真实输出 Y。现在,我们可以忘记这个过滤器了。我们将使用梯度下降和 2D 卷积从数据中恢复它。
十、运行实验
通过连接所有部分,我们最终可以看到训练执行情况:
int main() {
const int padding = 1;
auto dataset = load_dataset("../images/", padding);
const int MAX_EPOCHS = 1000;
const double learning_rate = 0.1;
auto history = gradient_descent(kernel, dataset, learning_rate, MAX_EPOCHS);
std::cout << "Original kernel is:\n\n" << std::fixed << std::setprecision(2) << Sobel.Gx << "\n\n";
std::cout << "Trained kernel is:\n\n" << std::fixed << std::setprecision(2) << kernel << "\n\n";
plot_performance(history);
return 0;
}The following sequence illustrates the fitting process:

一开始,内核充满了随机数。因此,在第一个纪元中,输出图像通常是黑色输出。
然而,在几个纪元之后,梯度下降开始使核拟合到全局最小值。
最后,在最后一个纪元中,输出几乎等于基本事实。此时,损失值渐近移动到最低值。让我们检查一下各时期的损失表现:
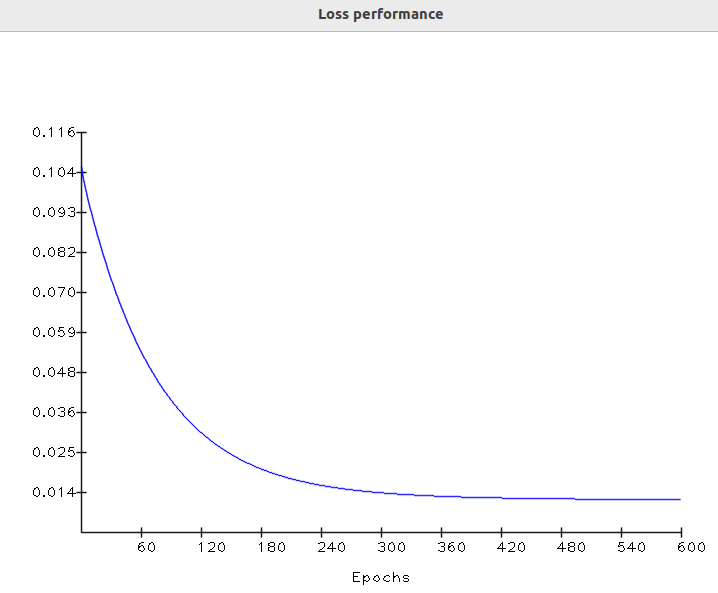
训练表现
在机器学习中,这种损失曲线形状非常常见。事实证明,在第一个纪元中,参数基本上是随机值。这会导致初始损失很高:

成本面上的算法搜索表示
在最后一个时期,梯度下降终于完成了它的工作,将核拟合到合适的值,这使得损失收敛到最小值。
现在,我们可以将学习到的内核与原始 Gx Sobel 的过滤器进行比较:
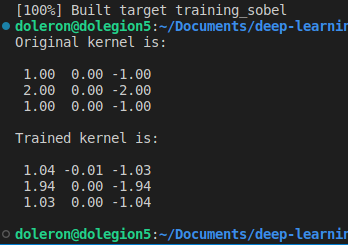
正如我们所料,学习内核和原始内核非常接近。请注意,如果我们在更多的时期训练内核(并使用较小的学习率),这种差异仍然可以更小。
用于训练此内核的代码可以在此存储库中找到。
十一、关于差异化和autodiff
在这个故事中,我们使用常见的微积分规则来查找MSE偏导数。然而,在某些情况下,为给定的复数成本函数找到代数导数可能具有挑战性。幸运的是,现代机器学习框架提供了一个神奇的功能,称为自动微分或简称。autodiff
autodiff跟踪每个基本算术运算(如加法或乘法),将链式规则应用于它们以找到偏导数。因此,在使用时,我们不需要计算偏导数的代数公式,甚至不需要直接实现它们。autodiff
由于这里我们使用的是简单的、众所周知的成本公式,因此不需要手动使用甚至解决复杂的微分。autodiff
更详细地涵盖导数、偏导数和自动微分值得一个新的故事!
十二、结论
在这个故事中,我们学习了如何使用梯度来拟合数据中的内核。我们介绍了梯度下降,它简单、强大,是推导出更复杂的算法(如反向传播)的基础。我们还使用梯度下降法进行了一项实际实验,从数据中恢复了Sobel滤波器。
参考书
机器学习,米切尔
Cálculo 3, Geraldo Ávila(巴西葡萄牙语)
神经网络:综合基础,Haykin
模式分类,杜达
计算机视觉:算法和应用,Szeliski。
Python machine learning, Raschka