链接:

105. 从前序与中序遍历序列构造二叉树

先序

能够确定谁是根

中序

知道根之后，能够确定左子树和右子树的范围

例子

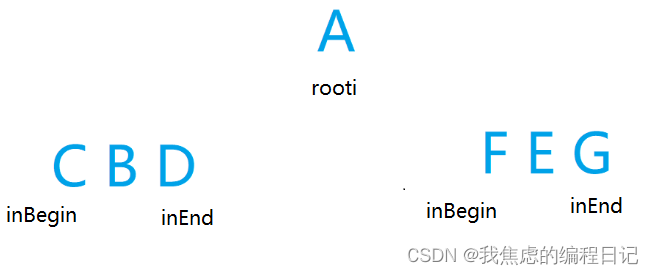
根据先序的性质（根左右），能够确定根，我们就能够从总序中找出根节点（rooti所在的结点）。

1. 先序的第一个是A，所以这棵树的根节点是A
2. 那么从中序中找出A，分布于A左右两侧的结点就是左右子树的范围

CBD 就是A的左子树（但是具体哪个是左子树根并不确定），右子树FEG同理。

3. 示意图：
4. （先找左边是因为先序：根完了是左，而不是右) 接着我们找A.left：从先序中找到第一个在CBD范围中的是B，A.left的根是B
5. 构建A.left示意图：
   
6. 下一步应该构建B.left：inEnd变为rooti-1，与inBeign相遇，标志着到达叶子结点，仍应创建C结点，构造到B的左边，即B.left。

在此时应该考虑一种此题中未出现的情况：
如果本题中没有C结点（即中序为BDAFG），那么inBegin仍会停留在未分叉的rooti位置，但是inEnd仍会走到rooti-1（是-1下标），这时会造成越界。
所以对这种情况需要进行筛选：

if (inBegin > inEnd)   return null;

代码：

class Solution {
    // preIndex是局部变量的时候，递归不是想要的一直++的值
    // 所以设置为成员变量
    public int preIndex = 0;

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder, inorder, 0, inorder.length-1);
    }
    // 需要写新函数进行递归构造
    public TreeNode buildTreeChild(int[] preorder, int[] inorder, int inBegin, int inEnd) {
        // 1. 除了inBegin > inEnd 这种情况（没有左/右子树），其他的都应该新建结点进行构造
        if (inBegin > inEnd) {
            return null;
        }
        // 2. 找到根节点，创建
        TreeNode root = new TreeNode(preorder[preIndex]);

        // 3. 找到root下标
        int rooti = findRootIndex(inorder, inBegin, inEnd, preorder[preIndex]);
        // 如果没有找到根节点
        if (rooti == -1) {
            return null;
        }

        // 继续向后找根节点
        preIndex++;

        // 4. 递归构造
        // 先构建左子树, 左端点是inBegin,右端点是rooti-1
        root.left = buildTreeChild(preorder, inorder, inBegin, rooti-1);
        // 再构建右子树
        root.right = buildTreeChild(preorder, inorder, rooti+1, inEnd);

        return root;
    }

    // 在给定区间中找到key，返回rooti（下标）
    public int findRootIndex(int[] inorder, int inBegin, int inEnd, int key) {
        for (int i = inBegin; i <= inEnd; i++) {
            if (inorder[i] == key) {
                return i;
            }
        }
        // 没找到
        return -1;
    }
}