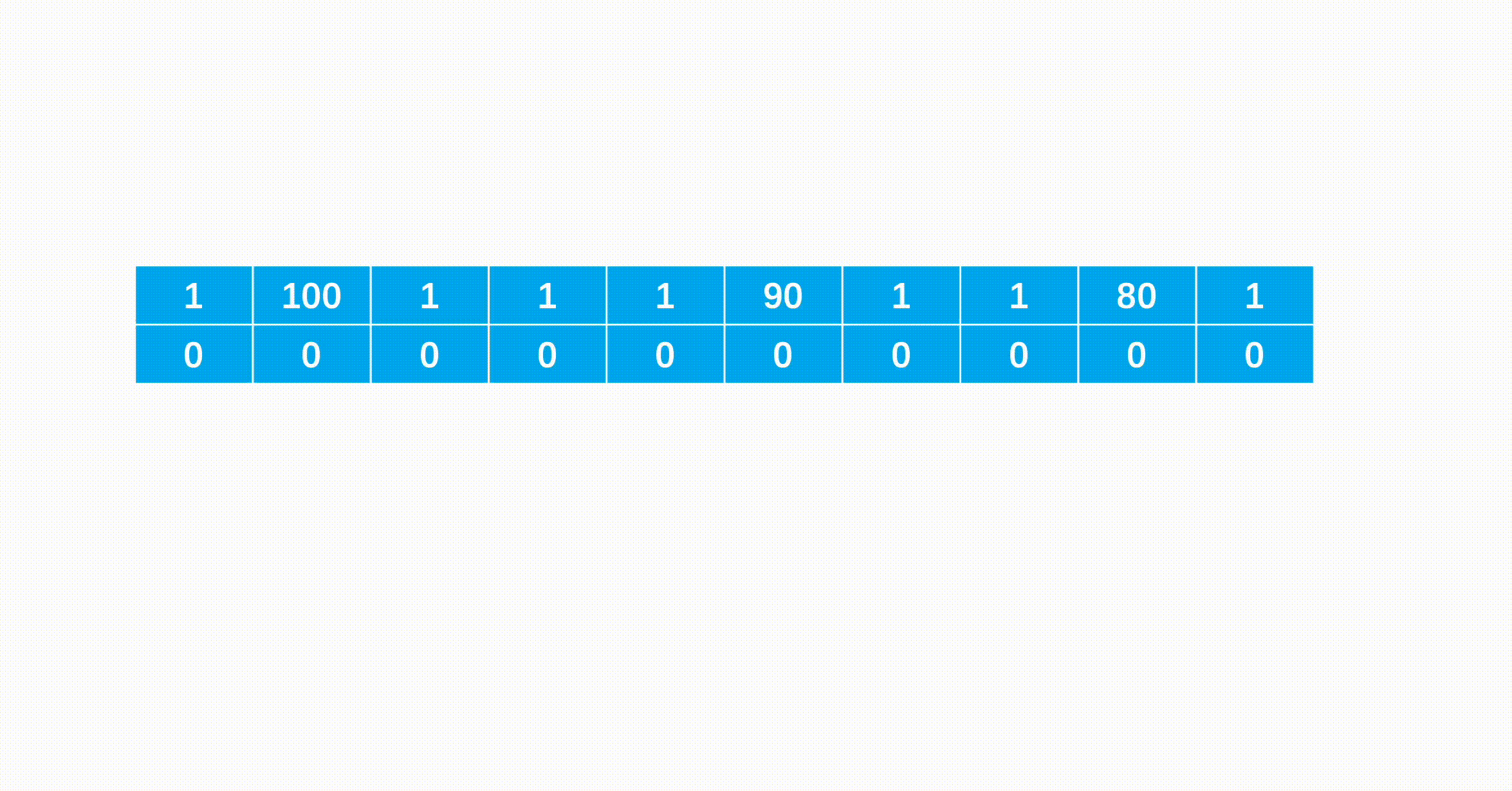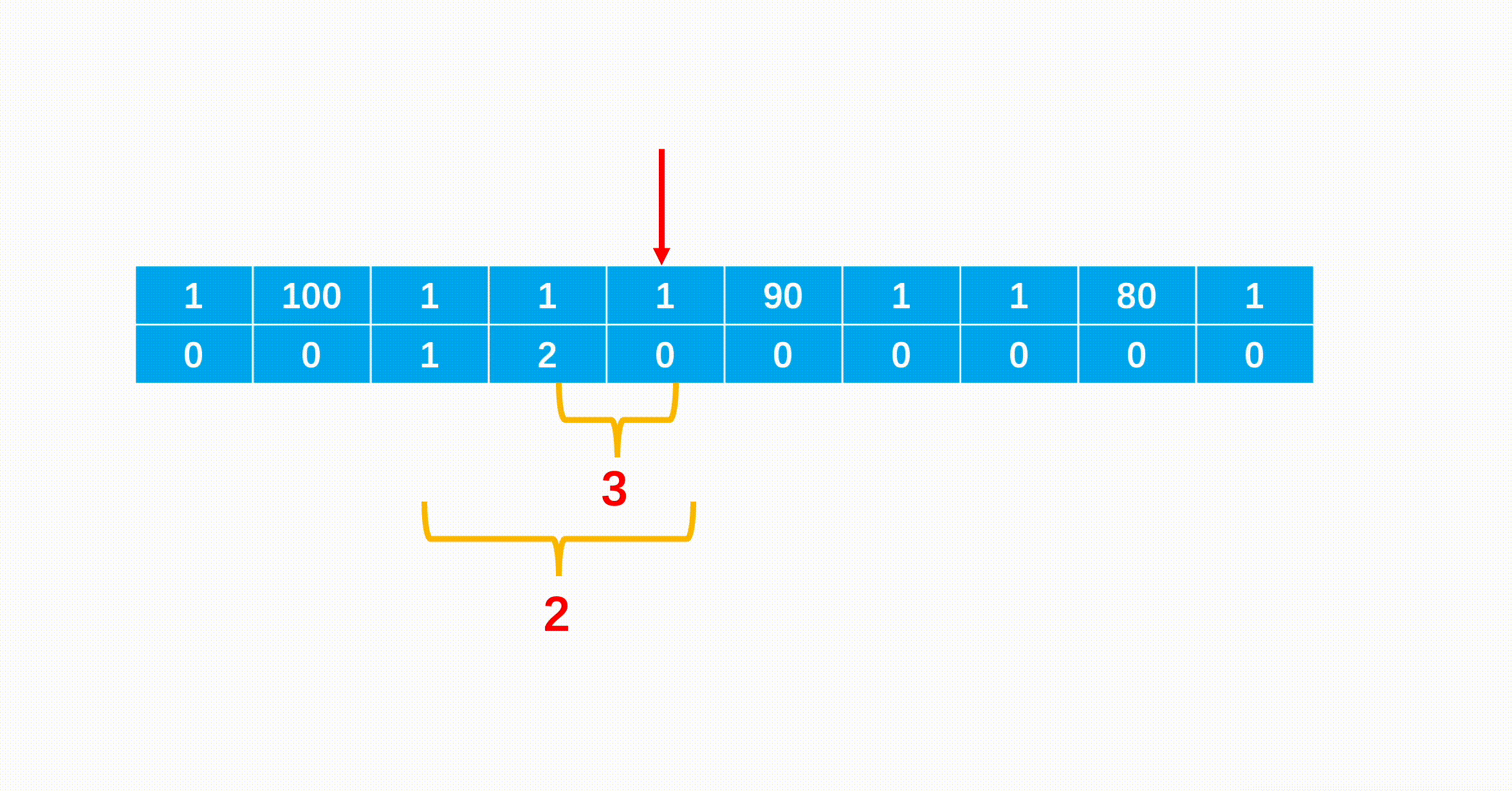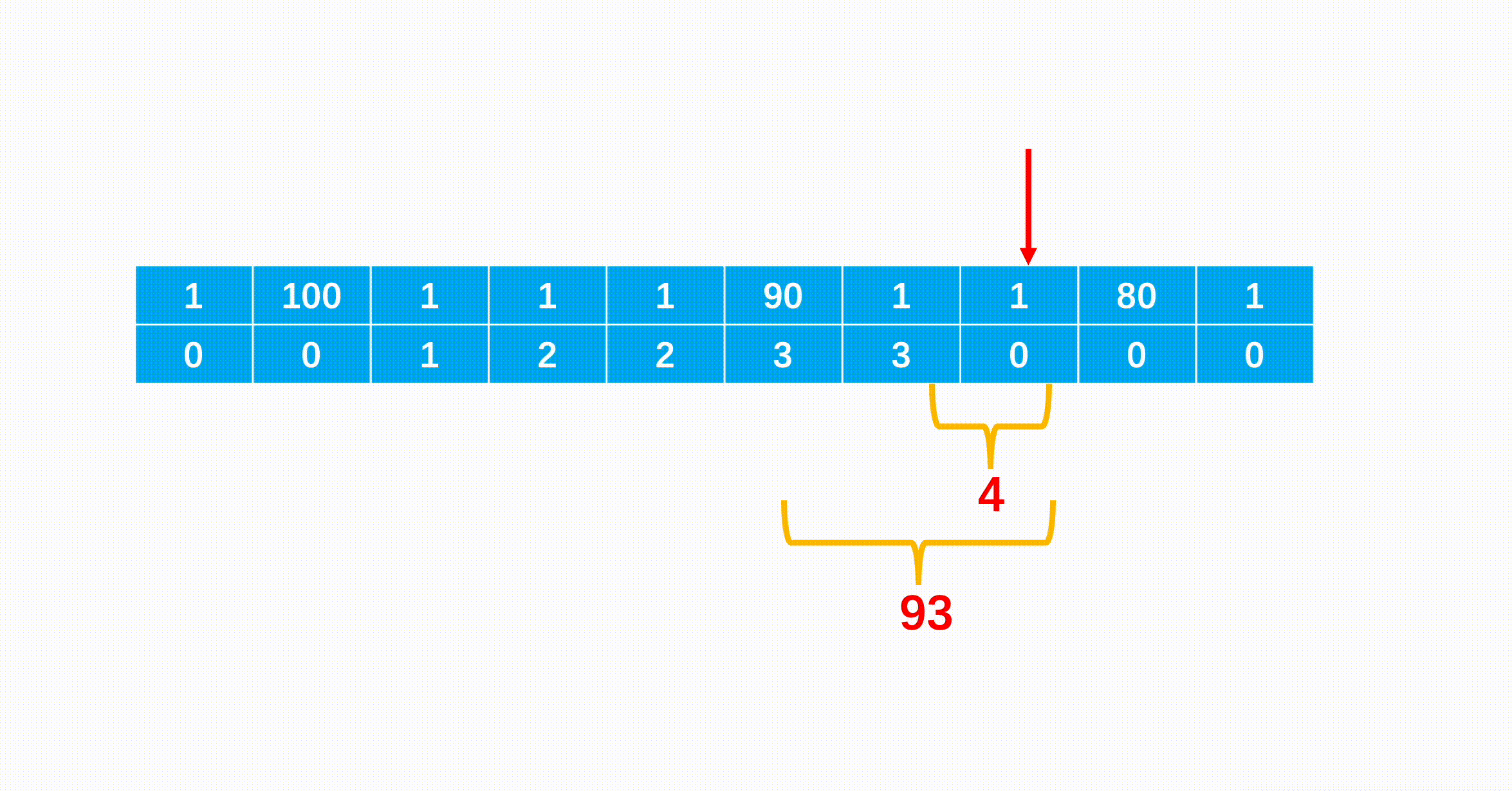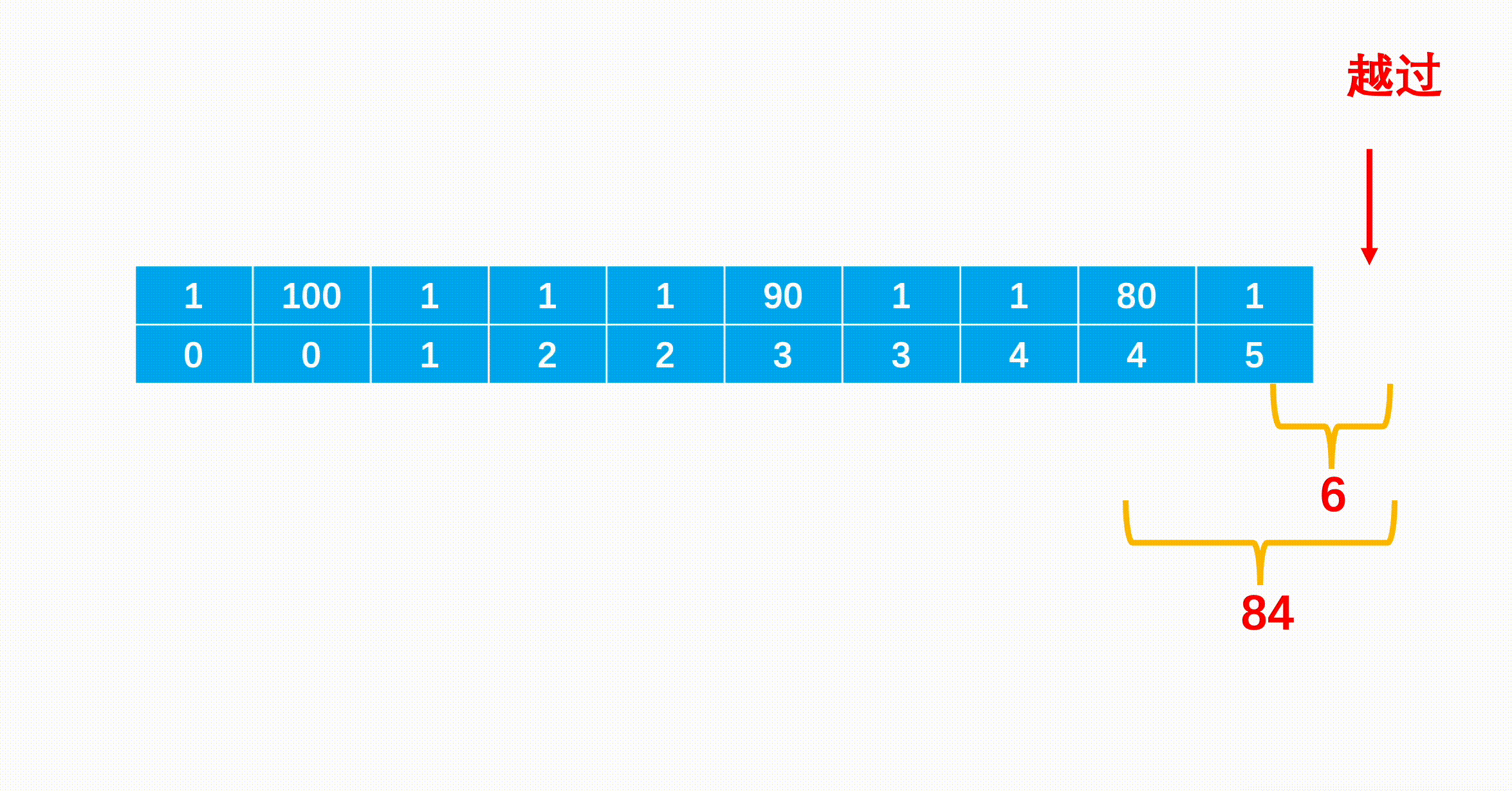
这道题我知道要用位运算，想了一下没头绪就直接看题解了，就是所有元素进行异或操作，对于两个操作数的每一位，相同结果为0，不同结果为1，在计算过程中，成对出现的数字的所有位会凉凉抵消为0，最终得到的结果就是那个出现了一次的数字。

进一步改进这个方法，可以把所有数字分成两组，使得：1，两个不同的数字在不同的组中；2，所有相同的数字在同一组中。

假设这两个不同的数字是a和b，那么所有数字异或的结果就是a和b异或的结果，记这个数为x，x的二进制形式是XkXk-1……X1X0，Xi=1或0，Xi=1表示a和b在第i位上不等，Xi=0表示a和b在第i位相等。然后我们选择一个Xi=1的i，通过第i位的是0还是1把数字分成两组，是0的在一组，是1的在另一组，这样就做到了那两个条件，a和b在不同的组（因为a和b的第i位不同），相同的数在同一组（因为相同的数所有位都相同，第i位相同就在同一组）。

最后只要在每个组内自己全部元素相与，相同的数会两两抵消，最后只剩a另一组只剩b，把a，b放在数组返回即可。

class Solution {
    public int[] singleNumbers(int[] nums) {
       int ret = 0;
       for(int n : nums){
           ret ^= n;
       } 
       int div = 1;
       while((div & ret) == 0){
           div <<= 1;
       }
       int a =0, b =0;
       for(int n : nums){
           if((div & n) != 0){
              a ^= n;
           }else{
              b ^= n;
         }
       }
       return new int[]{a, b};
    }
}