具体dijkstra算法就不展开说了,因为太多帖子来解释了,并且这也只是我的个人总结/记录,我会把自己的思考过程写在代码的注释中。
743. 网络延迟时间(有向图)
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
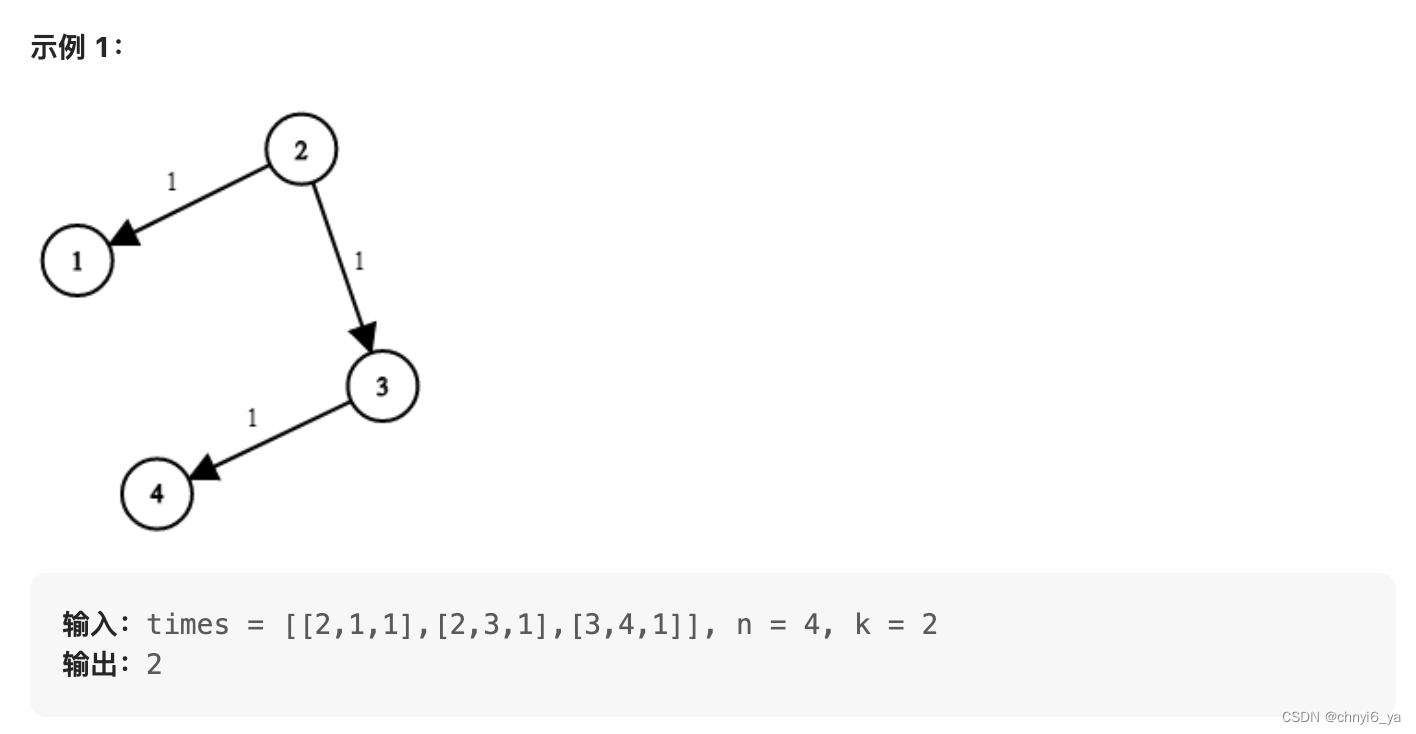
1. 邻接表法
class Solution {
public:
// distances数组 保存:起点k 到其他点的最短距离
// visited数组 保存:某点是否被访问过了,被访问过则设置为true
// graph 二维数组:邻接表
// n : 节点总数
void dijkstra(vector<vector<long long>>& graph,vector<int>& distances,int n,int k,vector<bool>& visited){
distances[k] = 0;// 起始点到起始点自身的距离为0
// 这里只需要循环 n-1次
// 原因:除k点以外只有 n-1个点,每循环一次,就更新k点到一个点的距离
for(int i = 1;i<=n-1;i++){
int id = 0,minDistance = INT_MAX;
for(int j = 1;j<=n;j++){
// 这个循环的目的:去找 距离 k点最近的点
// 原因:可以通过 这个点,去更新 其他点到 k点的距离
if(!visited[j] && distances[j]<minDistance){
minDistance = distances[j];
id = j;
}
}
// 所有点都被访问过了 或者 所有点都不可达
if(id == 0) return;
visited[id] = true;
// 得到一个中间点 id后,比较k->id->某一点的距离 和 k->某一点的距离
// 来更新distances数组,注意,这个数组存的是k到某一点的距离
for(int j = 1;j<=n;j++){
if(!visited[j] && distances[id]+graph[id][j]<distances[j]){
distances[j] = distances[id]+graph[id][j];
}
}
}
}
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<vector<long long>> graph(n+1,vector<long long>(n+1,INT_MAX));
vector<int> distances(n+1,INT_MAX);
vector<bool> visited(n+1,false);
// 建立邻接表
for(auto t:times){
int u = t[0],v = t[1],w = t[2];
graph[u][v] = w;
}
//dijkstra算法
dijkstra(graph,distances,n,k,visited);
int ans = 0;
for(int i = 1;i<=n;i++){
if(distances[i] == INT_MAX) return -1;
ans = max(ans,distances[i]);
}
return ans;
}
};
2. 优先队列
class Solution {
public:
void dijktra(vector<vector<int>>& times,vector<int>& dis, int n, int k){
dis[k] = 0;
using Pair = pair<int,int>; // first是距离,second是目标点
priority_queue<Pair,vector<Pair>, greater<Pair>> pq;
pq.push({0,k});
while(!pq.empty()){
auto e = pq.top();
pq.pop();
if(e.first>dis[e.second]) continue;
for(int i = 0;i<times.size();i++){
if(times[i][0] == e.second){
int v = times[i][1];
// 到v点的的距离
int w = e.first+times[i][2];
if(dis[v]==-1 || dis[v]>w){
dis[v] = w;
pq.emplace(w,v);
}
}
}
}
}
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
vector<int> dis(n+1,-1);
dijktra(times,dis,n,k);
int ans = 0;
for(int i = 1;i<=n;i++){
if(dis[i]==-1) return -1;
ans = max(ans,dis[i]);
}
return ans;
}
};
1334. 阈值距离内邻居最少的城市
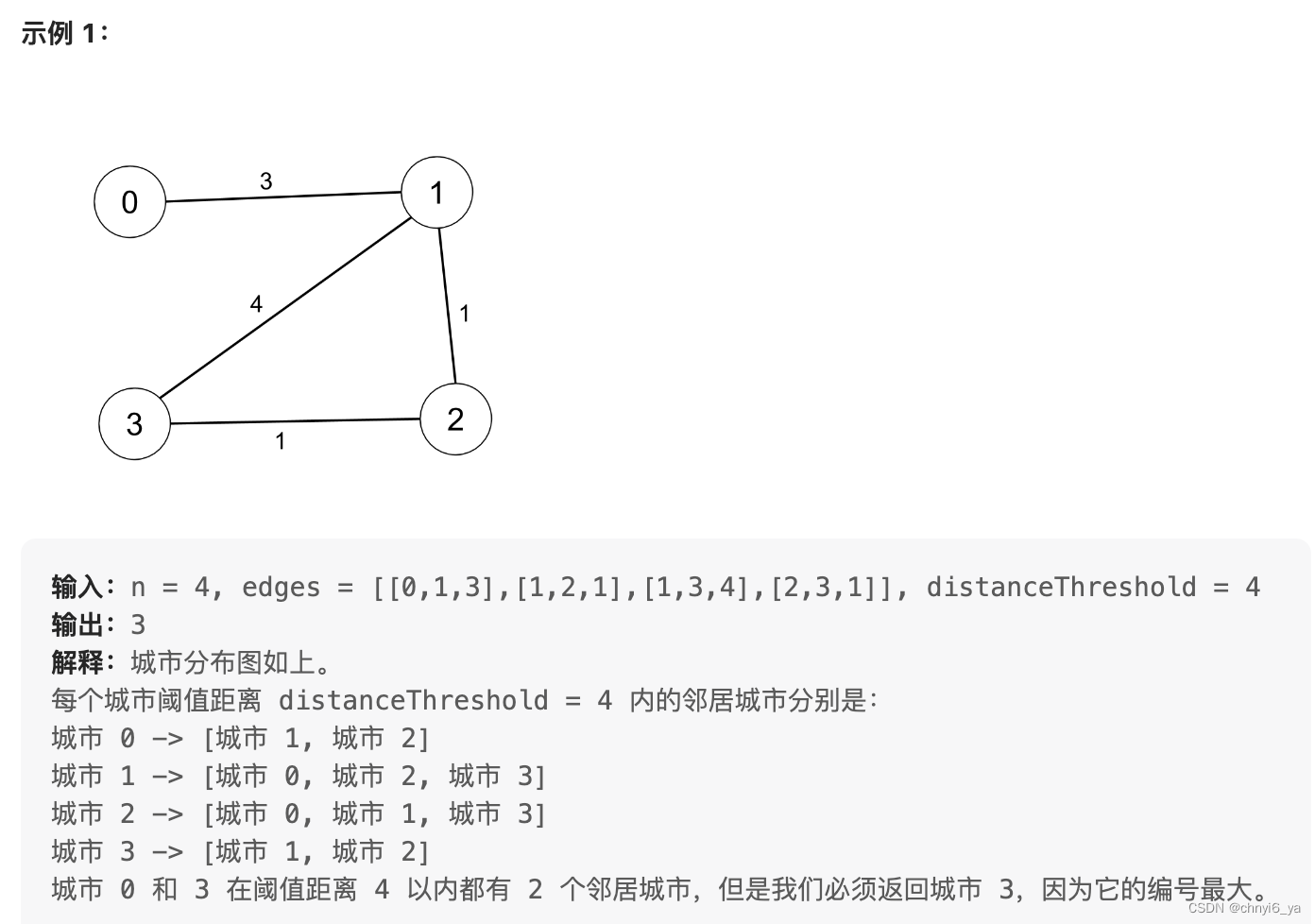
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
1. 邻接表法
class Solution {
public:
void Dijkstra(vector<vector<long long>>& graph,vector<int>& distances,vector<bool> &visited,int n,int distanceThreshold,int start){
// 自身到自身的距离为0
distances[start] = 0;
for(int i = 0;i<n-1;i++){
int u = -1,minDis = INT_MAX;
// 下面这个这个循环的目的:
// 为了在 和 start 点相连的所有点中找到一个最近的点,再把它设为新的起点
for(int j = 0;j<n;j++){
if(!visited[j] && distances[j] <minDis){
u = j; // 设置新的起点
minDis =distances[j];
}
}
// 如果所有点都访问过了 或者 不可达,直接return 即可
if(u==-1) return;
// 把新的起点设置为访问过
visited[u] = true;
// 接下来更新 start到所有点的 新的 距离
// 为什么有新的距离?
// 回答:因为此时我们有了一个新的点,那么从 start点开始到其他点就不止一种直连路线
// 而是可以借助 刚刚确立好的新的点 ,比如从 start到某点 需要距离为5
// 而start 到 u 的距离为1,u到某点的距离为2,那么就可以更新新的距离了
for(int j = 0;j<n;j++){
// 注意:仍然需要不去管那些已经访问过的节点
//因为已经访问过的节点就已经是最短的距离了
if(!visited[j] && distances[u]+graph[u][j]<distances[j]){
distances[j] = distances[u]+graph[u][j];
}
}
}
}
// 使用Dijkstra算法,邻接矩阵版
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<long long>> graph(n,vector<long long>(n,INT_MAX));// 邻接矩阵
for(auto edge:edges){
int u = edge[0],v = edge[1],w = edge[2];
graph[u][v] = graph[v][u] = w;
}
// minCount:在指定的阈值内可以 到达节点 的最少数量
int idx = -1,minCount = INT_MAX;
for(int i = 0;i<n;i++){
vector<int> distances(n,INT_MAX);// 单源最短路径数组
vector<bool> visited(n,false); // 用来记录某一节点是否被访问过
// 调用函数可以得到从i点出发到其他各个点的最短距离
// 这些距离被保存在distances数组中
Dijkstra(graph,distances,visited,n,distanceThreshold,i);
int count = 0; // 小于等于阈值的城市个数
for(int j = 0;j<n;j++){
if(i!=j && distances[j] <= distanceThreshold ){
count++;
}
}
if(count<=minCount){
minCount = count;
// 保存当下这个出发点
idx = i;
}
}
return idx;
}
};
2. 优先队列
class Solution { //优先队列版
public:
void Dijkstra(vector<vector<int>>& graph, vector<int>& distances, int n, int distanceThreshold, int start) {
//小顶堆,按照距离dist从小到大排序,pair中first存dist
priority_queue <pair<int, int>,vector<pair<int, int>>, greater<pair<int, int>>> q;
distances[start] = 0;
q.push({distances[start],start});
while (!q.empty()) {
pair<int, int>p = q.top();
int u = p.second;
q.pop();
if (distances[u] < p.first) {
continue;
}
for (int v=0; v<n; ++v) {
if (graph[u][v] != INT_MAX && distances[v]>distances[u]+graph[u][v]) {
distances[v]=distances[u]+graph[u][v];
q.push({distances[v],v});
}
}
}
}
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<int>>graph(n,vector<int>(n,INT_MAX)); //邻接矩阵
for (vector<int> edge : edges) {
int u=edge[0], v=edge[1], w=edge[2];
graph[u][v] = graph[v][u] = w;
}
int idx = -1, minCount = INT_MAX;
for (int i=0; i<n; ++i) {
vector<int>distances(n,INT_MAX); //单源最短路径数组
Dijkstra(graph, distances, n, distanceThreshold, i);
int count = 0; //小于等于距离阈值的城市个数
for (int j=0; j<n; ++j) {
if (distances[j]<=distanceThreshold && i!=j) {
count++;
}
}
if (count <= minCount) {
minCount = count;
idx = i;
}
}
return idx;
}
};
最后:
其实dijkstra算法(邻接表版本)对有向图和无向图使用起来都是一样的,没有区别。我之前会想如果我把[0,3,2]中的0和3调换会不会情况不一样,答案是不会的。因为在建邻接表的时候,就把双向的距离给设置好了,如果调换顺序,不过是从另一个点出发,距离仍然一样,并且也不用担心重复访问的问题,因为使用了visited数组来区分。