1.题目：

69. x 的平方根(Easy)

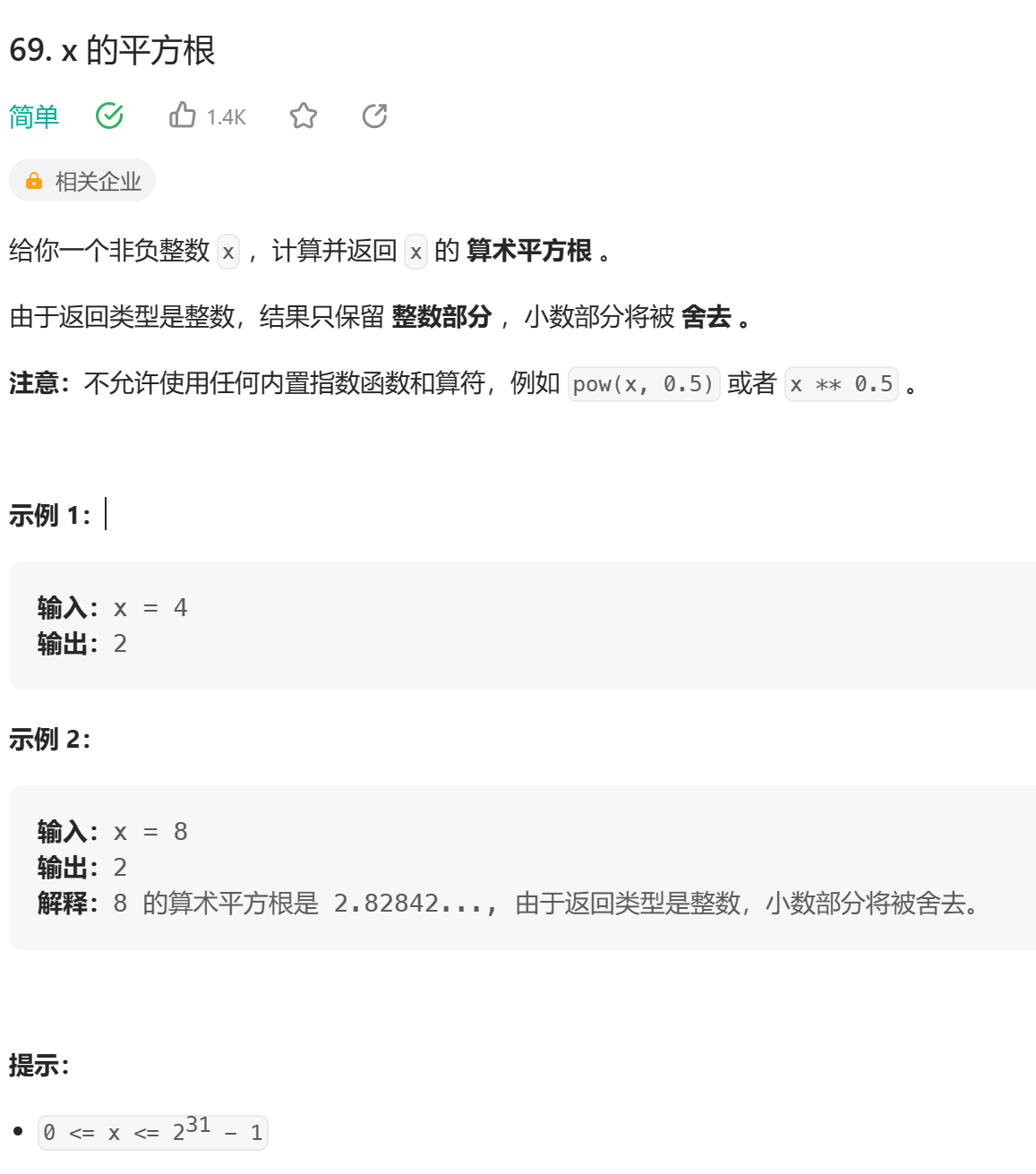
1.代码：

class Solution:
    def mySqrt(self, x: int) -> int:
        # 思路：二分法，左闭右开
        # 额外添加1：判断0，1是否符合；
        if x == 0 or x ==1 :
            return x
        left , right ,res = 0 , x ,-1           # res 是为了记录返回最小，题解说为-1，防内存溢出？
        while left < right :
            mid = left + (right-left)//2        
            if mid**2 <= x:          #额外添加2： <  →  <=  因为返回的值平方小于等于x即可
                left = mid + 1
                res = mid            #记录res 
            else :
                right = mid
        return res

2.题目：

367. 有效的完全平方数（Easy）

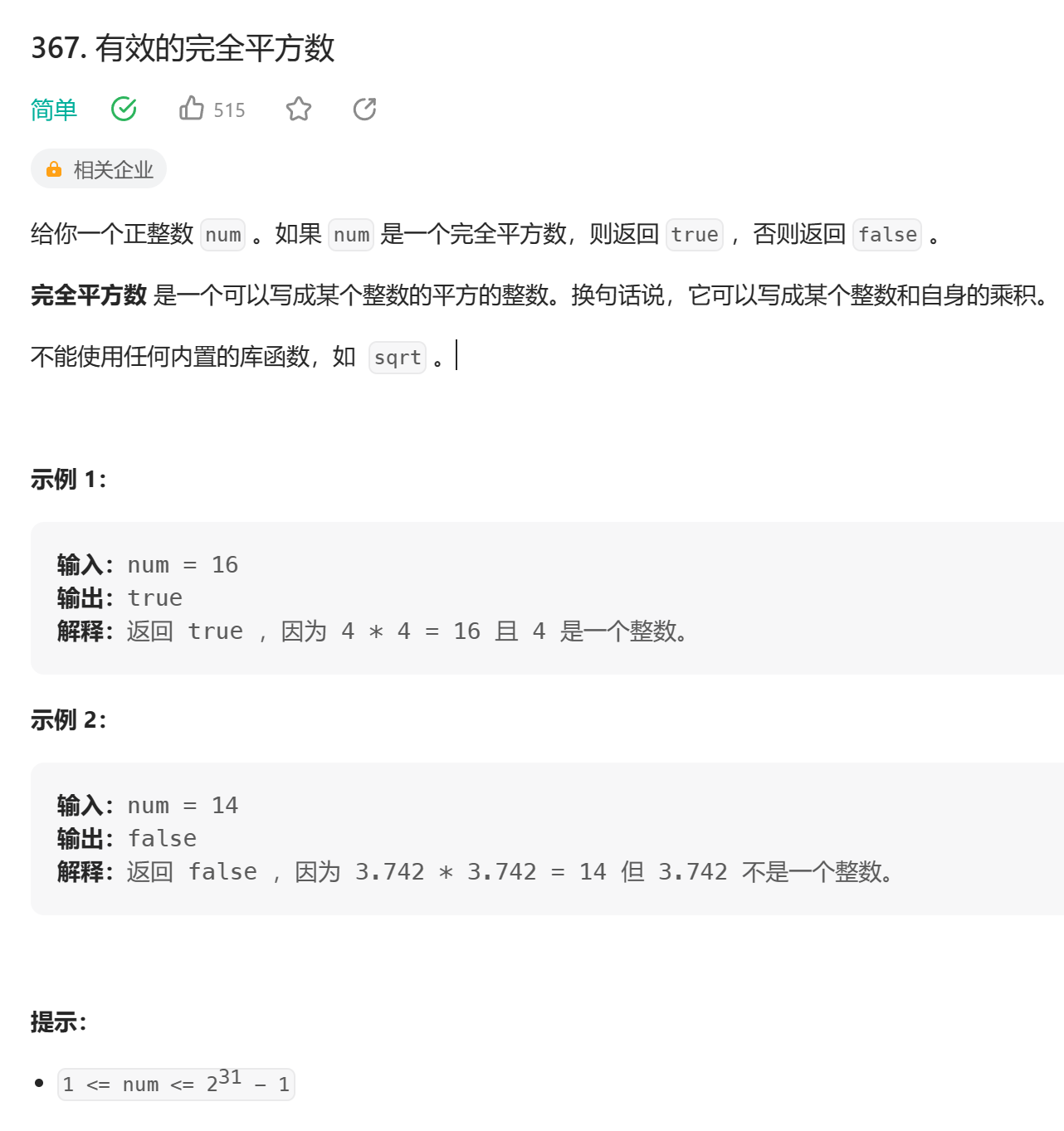
2.代码：

1.左闭右闭，分条件判断

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        # 二分法，考虑到需要相等，所以要用左闭右闭；
        left , right = 0 , num-1
        if num == 1 :           #下边漏掉了1，因为len-1 直接为0
            return True
        while left <= right:
            mid = left + (right-left)//2
            if mid**2 == num :
                return True
            elif mid**2 < num :
                left = mid +1 
            else: 
                right = mid -1
        return False

1.左闭右开 + 返回判断

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        # 二分法，左闭右开
        l,r = 1 ,num                #左边改为从1开始，因为为正整数的积
        while l < r :
            mid = l + (r-l)//2
            if mid**2 < num:
                l = mid + 1
            else :
                r = mid
        # 前边就是普通左闭右开二分法，最后一个神来之笔！！！
        # 比我漏条件 + 多条件 return 好的多    ！！！   
        return l*l == num