Acwing.883 高斯消元解线性方程组

news2024/12/28 2:12:27

题目

输入一个包含n个方程n个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含m个方程n个未知数的线性方程组示例:

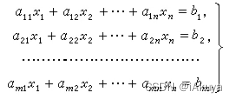
在这里插入图片描述

输入格式

第一行包含整数n。
接下来n行，每行包含n+1个实数，表示一个方程的n个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共n行，其中第i行输出第i个未知数的解，结果保留两位小数。如果给定线性方程组存在无数解，则输出"Infinite group solutions"。
如果给定线性方程组无解，则输出"No solution"。

数据范围

1<n ≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过100。

输入样例

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1,00 -1,00 2.00 7.00

输出样例

1.00
-2.00
3.00

题解

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 110;
/*  C++浮点数存在误差，不能直接判断0，要判断是否小于一个很小的数，
    如果小于这个很小的数，就认为是0，如小于1e-6*/
const double eps = 1e-6;

int n;
double a[N][N];


int gauss()
{
    int c, r;// c列，r行
    for (c = 0, r = 0; c < n; c ++ )
    {
        int t = r;
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        if (fabs(a[t][c]) < eps) continue;
        

        for (int i = c; i < n + 1; i ++ ) swap(a[t][i], a[r][i]);

        for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];
        
   
        for (int i = r + 1; i < n; i ++ )
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j -- )
                    a[i][j] -= a[r][j] * a[i][c];

        r ++ ; 
    }
    
    // 无解和无穷多解的判断
    if (r < n)
    {
        // 如果出现了等号左右一个为0一个非0，则说明无解
        for (int i = r; i < n; i ++ )
            if (fabs(a[i][n]) > eps)
                return 2;
        // 否则说明有无穷多解
        return 1;
    }
    
    for (int i = n - 1; i >= 0; i -- )
        for (int j = i + 1; j < n; j ++ )
            a[i][n] -= a[j][n] * a[i][j];
    
    return 0;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n + 1; j ++ )
            cin >> a[i][j];
    int t = gauss();
        if (t == 0)
    { 
        for (int i = 0; i < n; i ++ ) printf("%.2lf\n", a[i][n]);
    }
    else puts("No solution");
    return 0;
}