文章地址: https://ieeexplore.ieee.org/document/9577798/footnotes#footnotes

参考博客: https://github.com/PangTongyao/Recorrupted-to-Recorrupted-Unsupervised-Deep-Learning-for-Image-Denoising

1. 方法原理

1.1 相关研究

Noise2Noise的问题

• 噪声图像对不好获取
• 同一场景不同图像怎么对齐？

解决N2N配对问题的工作可以分为两类

• 数据增强方法：

  • Noise2Void 和 Noise2Self使用盲点网络的方法避免过拟合（直接点到点映射）
  • Noiser2Noise 和 Noise-as-Clean 是采样额外的噪声数据配对进行训练

• 正则化去噪的DNN：

  • Stein’s Unbiased Risk Estimator（SURE）通过添加对预测结果散度的惩罚添加正则
  • Deep Image Prior 使用 early-stopping 防止过拟合
  • Self2Self中使用 Dropout引入不确定性估计，提高去噪的鲁棒性。

研究动机

• 无监督/自监督学习在实际工作、缺少干净数据的时候是非常有效的
• 现有的无监督方法还无法和监督学习媲美

---

1.2 研究思路

从可加性的高斯噪声出发，配对的噪声数据对科比表示为
$$\begin{array}{rl}y& =x+nn\sim N(0,{\sigma }_1^{2}I)\\ y^{\prime }& =x+n^{\prime }{n}^{\prime }\sim N(0,{\sigma }_2^{2}I)\end{array}$$

Noise2Noise的L2损失函数需要优化
E n , n ′ { ∣ ∣ F θ ( y ) − y ′ ∣ ∣ 2 2 } E_{n,n'}\{ ||F_{\theta}(y) - y'||_2^2\} En,n′​{∣∣Fθ​(y)−y′∣∣22​}

将其展开进行推导
E n , n ′ { ∣ ∣ F θ ( y ) − y ′ ∣ ∣ 2 2 } = E n , n ′ { ∣ ∣ F θ ( y ) − x − n ′ ∣ ∣ 2 2 } = E n , n ′ { ∣ ∣ F θ ( y ) − x ∣ ∣ 2 2 − 2 ( n ′ ) T ( F θ ( y ) − x ) + ( n ′ ) T n ′ } = E n , n ′ { ∣ ∣ F θ ( y ) − x ∣ ∣ 2 2 } − 2 E n , n ′ { ( n ′ ) T F θ ( y ) } + c o n s t \begin{aligned} &E_{n,n'}\{ ||F_{\theta}(y) - y'||_2^2\} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x - n'||_2^2\} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x||_2^2 - 2(n')^T(F_{\theta}(y) -x) + (n')^Tn' \} \\ &= E_{n,n'}\{ ||F_{\theta}(y) - x||_2^2\} - 2E_{n,n'}\{ (n')^T F_{\theta}(y)\} + const \end{aligned} ​En,n′​{∣∣Fθ​(y)−y′∣∣22​}=En,n′​{∣∣Fθ​(y)−x−n′∣∣22​}=En,n′​{∣∣Fθ​(y)−x∣∣22​−2(n′)T(Fθ​(y)−x)+(n′)Tn′}=En,n′​{∣∣Fθ​(y)−x∣∣22​}−2En,n′​{(n′)TFθ​(y)}+const​

如果噪声 $n$ 和 $n^{\prime }$ 是独立的，那么 $E_{n,n^{\prime }}\{(n^{\prime }{)}^T{F}_{\theta }(y)\}=0$，也就是说噪声对监督学习和噪声-干净数据的监督学习可以得到相同的优化结果。现在的问题就是如何从一张噪声图片（$y$）中构建出一对具有独立噪声的数据($\hat{y},\tilde{y}$)

根据假设，噪声的分布是 AWGN（additive white Gaussian noise），那么噪声服从分布 $n\sim N(0,{\sigma }_1^{2}I)$。 现在根据下方的方法进行采样
$$\hat{y}=y+D^{T}z,\tilde{y}=y-D^{-1}z,z\sim N(0,{\sigma }_1^{2}I)$$

其中D可以是任何可逆矩阵，文章中证明了 噪声样本$\hat{y}$和$\tilde{y}$相互独立，所以根据这两个样本训练的网络满足
E n , z { ∣ ∣ F θ ( y ^ ) − y ~ ∣ ∣ 2 2 } = E n ^ { ∣ ∣ F θ ( x + n ^ ) − x ∣ ∣ 2 2 } E_{n,z}\{||F_{\theta}(\widehat{y}) - \widetilde{y}||_2^2\} = E_{\widehat{n}} \{ ||F_{\theta}(x + \widehat{n}) - x||_2^2 \} En,z​{∣∣Fθ​(y ​)−y ​∣∣22​}=En ​{∣∣Fθ​(x+n )−x∣∣22​}

其中 $\hat{n}=n+D^{T}z$

那么对于这种无结构噪声数据：
$$y^k=x^k+n^k,x^k\sim X,n^k\sim N(0,{\sigma }^{2}I)$$

用噪声数据对 {$({\hat{y}}^k,{\tilde{y}}^k)$}定义的损失函数为也就等价于下面这个损失函数了
E x , n ^ { ∣ ∣ F θ ( x + n ^ ) − x ∣ ∣ 2 2 } E_{x,\widehat{n}}\{ ||F_{\theta}(x + \widehat{n}) - x||_2^2\} Ex,n ​{∣∣Fθ​(x+n )−x∣∣22​}

对于结构化的噪声数据，可以调整噪声数据的表示形式：比如噪声的分布和干净数据相关
n服从 $N(0,{\sum }_x)$的正态分布，可以将噪声对表示为

$$\hat{y}=y+\sqrt{\sum _x}{D}^{T}z,\tilde{y}=y-\sqrt{\sum _x}{D}^{-1}z,z\sim N(0,I)$$

其中协方差差矩阵 ${\sum }_x$是正定矩阵，其满足 ${\sqrt{{\sum }_x}}^T=\sqrt{{\sum }_x},\sqrt{{\sum }_x}\sqrt{{\sum }_x}={\sum }_x$

1.3 小结

1. 从数学推导上证明了 R2R的方法和监督学习的可比性
2. 相比其他无监督去噪方法，该方法简单且灵活，也可以直接在噪声图像上进行处理
3. 去噪效果很好，在真实数据中也应用非常好

---

2. 实验结果

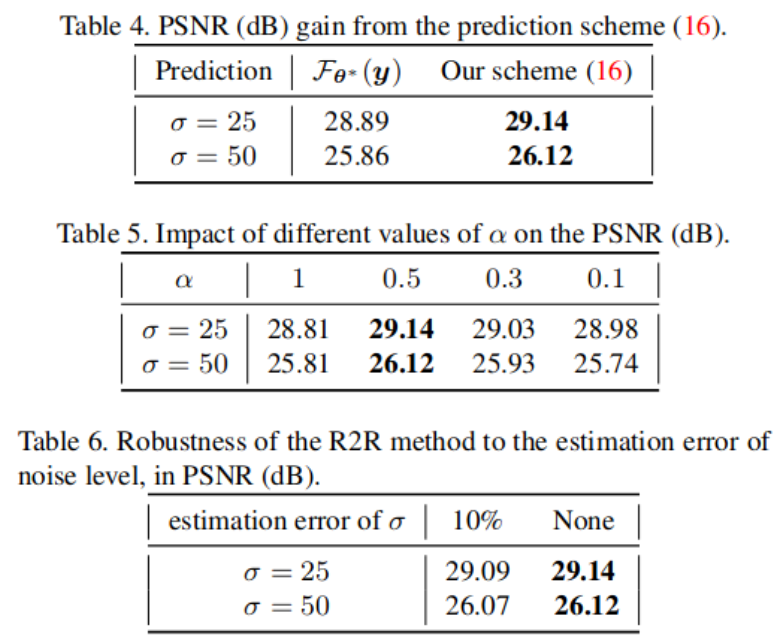
• 去除高斯噪声效果对比，R2R的效果比当前最好的 SURE 效果还要好。这里的 $D=\alpha I$ 和 $D^{-1}=I/\alpha$,其中 $\alpha =0.5$

  • 

• 去除真实图片中的噪声：噪声水平函数（noisy level function）给定，噪声函数建模为 heteroscedastic signle dependent Gaussian single, 其协方差为
  $$\sum _x=diag({\beta }_{1}x+{\beta }_2)$$
  设置 $D=2I,D^{-1}=I/2$。训练的结果展示R2R的效果在各种传统方法和无监督中是最好的，但是和监督学习仍然存在一定的差距。分析原因是：噪声模式和噪声水平函数的估计不准确

  • 

• 消融实验：比如对比不同的噪声水平的预测结果

  • 

3. 总结

优势：

1. 相比Noise2Noise：不需要配对噪声图片，而是根据一张噪声图片加噪
2. 相比Noiser2Noise：都是采样加噪，都需要估计噪声模式，但是本文的方法从数学上的推导更加严谨一些，同时也给定了如何加噪声的方式。
3. 相比Noise2Void，Noise2Self：作者对比了效果，会更好（我自己还需要补一个实验证明）
4. 这种方法可以应用到实际噪声之中，但是如何估计噪声模式是个大问题
5. 可以处理结构噪声和无结构噪声

缺点：

1. 需要估计噪声模式，网络会继承噪声模式估计的误差
2. 对于不同的噪声模式，其构建噪声对的方法会有所不同；
3. 对于不同的损失函数，这种方法是否也是需要修改？比如现在想要去除图片中的文字，那么使用L1损失函数明显是会比L2损失函数更有优势的。那么上面的推导是不是也需要相应地修改？