文章目录

前言

1. 题目一：环形链表Ⅱ

1.1 思路

1.2 分析

1.3 题解

1.4 方法二

2. 题目二：复制带随机指针的链表

2.1 思路

2.2 分析

2.3 题解

总结

前言

在这个专栏博客中，我们将提供丰富的题目资源和解题思路，帮助读者逐步提高解题能力。同时，我们也将分享一些刷题技巧和经验，帮助读者更加高效地进行刷题训练。通过持之以恒的努力和不断的实践，相信读者可以在数据结构领域取得长足的进步。本期将是数据结构刷题训练链表篇的最后一期，后续我们将进入栈和堆的刷题训练。

1. 题目一：环形链表Ⅱ

题目描述：

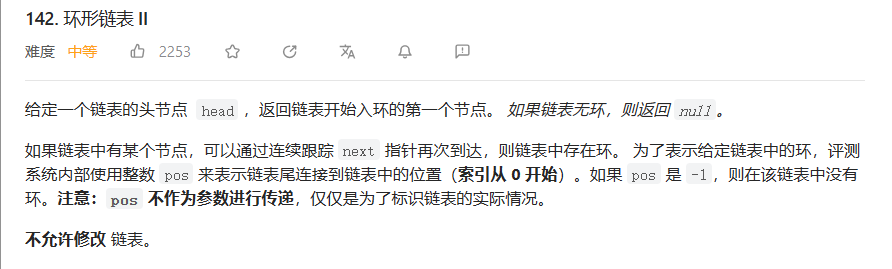
示例：

题目链接：环形链表Ⅱ

1.1 思路

本题的题意是：给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 NULL。

寻找第一个入环的节点，在上道环形链表的题目中仅仅只是判断是否有环，但没法确定入环的节点，这道题目属于之前题目的进阶。那我们要如何去解决呢？

这里向大家说明一点，如果在刷题的时候，遇到一个题目，连题意都很难理解或者，是无从下手，那这道题目就不再是简简单单的考察代码能力，其中的分析更为重要，没有分析的过程，仅仅只要代码是无法看懂理解的。

1.2 分析

初看题目毫无思路，但是别担心，我在分析之后记住这种做题思路、方法就可以，在后续刷题中灵活运用。这道题目我们仍然可以使用快慢指针的方法。

首先我们需要知道带环链表的几种情况：

一般情况：

环很大

环很小

在上期中我们将道使用快慢指针遍历链表，快指针一次走两步，慢指针一次走一步，如果它们相遇那它们一定是带环的链表。那问题来了，fast一次走两步，slow一次走一步，一定可以追上吗？ 结论是一定能追上。

为什么？我们可以分析一下，在两个指针都入环以后，快指针一次走两步，慢指针一次走一步，它们的距离会减一，一直走一直减一，最后直到追上，距离变化过程：

N

N-1

N-2

……

2

1

0

那如果fast一次走3步，slow一次走两步呢？

假设它们之间的距离是M，fast和slow都进环以后，它们的距离一次就是减2，那它们的距离变化：

M是偶数 M是奇数

M-2 M-2

M-4 M-4

…… ……

4 3

2 1

0 -1

如果M是偶数，就刚好追上相遇，如果M是奇数这就说明它们会错过，一旦错过就要继续走一圈，假设环的周长是C，当C为奇数时，当它们错过后，它们之间的距离是C-1，此时C-1必为偶数，下次一定能追上，但如果C是偶数时，C-1为奇数，然而它们每次距离减小2，这样无论怎么走都不会相遇。

如果继续增大步数呢？fast一次走4步，slow一次走两步。假设进入环后它们的距离是k，那么它们的距离变化：

k是3的倍数      k%3=2            k%3=1

k-3 k-3                  k-3

k-6   k-6 k-6

……                     …… ……

6 5 4

3 2 1

0 -1 -2

错过后距离： C-1 C-2

如果C-1或C-2仍然不是3的倍数，那它们仍然始终无法相遇。有人可能会这样想，那让其中一个停下来，另一个去追不就可以了，但我们无法确定慢指针是否进环了，如果没进环，那快指针走多少圈都不会追上。这里只是移动步数的分析，在带环链表中使用快慢指针，最好使用步数差为1的，下面步入正题：

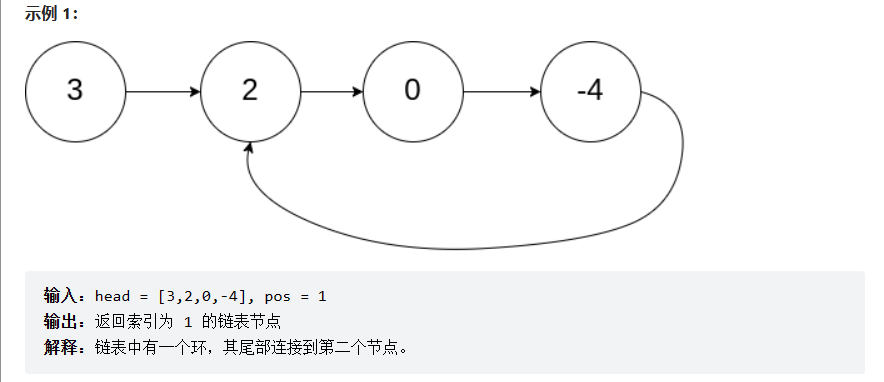
依据上述结论，我们看这道题目，这里我们让fast一次走2步，slow一次走1步，当fast入环时：

假设从起点到入环点距离为L，环周长为C

慢指针入环时：

相遇时：

由上可以得出：fast走的距离时slow的二倍，那slow走的距离就是X+L，那fast走的路程就是L+X+n*C（n>=0），因为无法确定L于C的关系，如果C很小，那fast就可能走了很多圈。或许有人会疑惑，那slow为什么不用加n*C，因为slow入环以后，fast在slow走一圈之内一定能追上它。

我们根据这些关系可以得到：

L+X+n*C=2（L+X）

化简一下：

L+X=n*C

n*C-X=L

得到n*C-X=L这个结论再转化一下就是：(n-1)*C+C-X=L

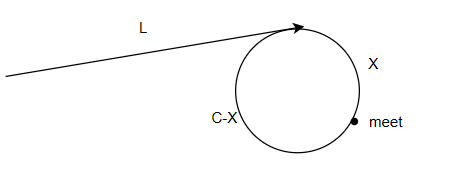
到这里就一目了然了，一个指针从相遇点开始出发，一个从起点开始出发，最终它们会在入环点相遇。

1.3 题解

根据上述的分析进行编写代码：

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* slow,*fast;
    slow=fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            struct ListNode* meet=slow;
            while(meet!=head)
            {
                head=head->next;
                meet=meet->next;
            }
            return head;
        }
    }
    return NULL;
}

1.4 方法二

方法二的思路简单，但代码量增多，我们先让两指针相遇，相遇后将相遇的节点的next置为NULL，也就是将环断掉，这样就转化成了链表相交。

代码如下：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{
    struct ListNode* curA=headA,*curB=headB;
    int lenA=1,lenB=1;
    while(curA->next)
    {
        curA=curA->next;
        lenA++;
    }
    while(curB->next)
    {
        curB=curB->next;
        lenB++;
    }
    if(curA!=curB)
    {
        return NULL;
    }
    int t= abs(lenA-lenB);
    struct ListNode* longlist=headA, *shortlist=headB;
    if(lenB>lenA)
    {
        longlist=headB;
        shortlist=headA;
    }
    while(t--)
    {
        longlist=longlist->next;
    }
    while(longlist!=shortlist)
    {
        longlist=longlist->next;
        shortlist=shortlist->next;
    }
    return longlist;
}
struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* slow,*fast;
    slow=fast=head;
    while(fast&&fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            struct ListNode* meet=slow;
            struct ListNode* newnode=meet->next;
            meet->next=NULL;

            return getIntersectionNode(newnode,head);
           
        }
    }
    return NULL;
}

2. 题目二：复制带随机指针的链表

题目描述：

示例：

题目链接：

复制带随机指针的链表

2.1 思路

或许大部分人读完题目还是像上道题目一样，读完没有思路，甚至连题意都读不懂。

复制一个链表不难，但这道题目的难点在于每个节点指针域的随机指针，我们很难控制随机指针的指向，单纯的完全复制行不通，复制下来的节点关系要与原链表相同，这才是本道题目的难点。

怎么才能找到随机指针的指向关系呢？

我们的思路是这样的：

遍历原链表，遍历一个节点复制一个节点，然后将复制的节点插入道原节点的后边。
再次遍历插入后的链表，找复制节点的随机指针的指向关系。
最后将复制的链表与原链表分开

2.2 分析

根据思路进行分析：

复制后的链表链接道原链表

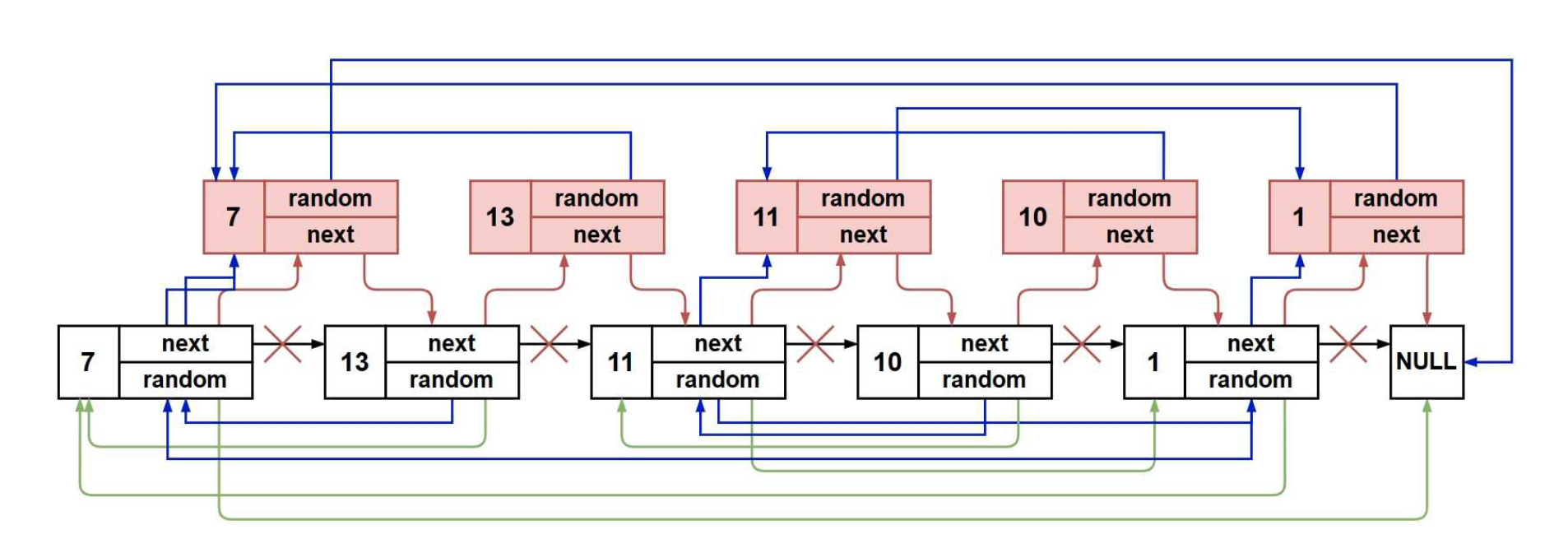
这里要理解如何去找复制节点的random指向的节点。

我们可以这样操作：copy->random=cur->random->next

重点就是这句的理解，cur指向的是原链表中的节点，复制的也就是cur指向的节点，然后将复制的节点（copy）链接到cur节点后，那copy节点的random不就在cur节点的random指向节点的下一个吗？

意思就是说，遍历原链表中的节点，找到当前节点的random就可以找到复制节点的random，因为复制节点（copy）的random，就是当前节点（原链表）random指向节点的下一个节点。

这里要好好理解，例如：13号这个节点（cur)，13节点的下一个节点就是复制的13号节点。cur的random指向的是7号节点（原链表），7号节点的下一个节点不就是复制的13号节点（copy）要找的random吗？

但这里需要特殊处理一种情况，就是原链表random指向为NULL的情况，这里就直接将复制节点的random置为NULL。

2.3 题解

根据上述的分析，开始编写代码：

struct Node* copyRandomList(struct Node* head)
{
	struct Node* cur=head;
    while(cur)                    //复制节点
    {
        struct Node* copynode=(struct Node*)malloc(sizeof(struct Node));
        struct Node* next=cur->next;
        copynode->val=cur->val;
        
        //插入到原节点后
        cur->next=copynode;
        copynode->next=next;
        
        cur=next;
    }
    cur=head;
    
//寻找复制节点的random
    while(cur)        
    {
        struct Node* copynode=cur->next;
        if(cur->random==NULL)        //随机指针为NULL进行特殊处理
        {
            copynode->random=NULL;
        }
        else
        {
            copynode->random=cur->random->next;
        }
        
        cur=cur->next->next;
    }
     cur=head;
     struct Node* copyhead,*copytail;
     copyhead=copytail=NULL;

//还原原节点，将两个链表分开
    while(cur)
    {
        
        struct Node* copynode=cur->next;
        struct Node* next=cur->next->next;
        //将复制节点链接到新的链表，这里使用的是无头节点的链表，所有需要特殊处理
        if(copyhead==NULL)
        {
            copyhead=copytail=copynode;
        }
        else
        {
            copytail->next=copynode;
            copytail=copytail->next;
        }
        //恢复原链表
        cur->next=next;
        cur=next;

    }
    return copyhead;
}