1.HashMap

1.1Hash的概念和基本特征

哈希(Hash)：也称为散列。就是把任意长度的输入，通过散列算法，变换成固定长度的输出，这个输出值就是散列值。

假设数组array存放的是1到15这些数，现在要存在一个大小是7的Hash表中，存储的位置计算公式是：

index = number % 7

在这里插入图片描述

对于如何取值，比如要取13，我们同样利用计算存储位置的计算公式13 % 7 = 6，我们访问array[6]，13是在的，返回true。如果想看20在不在哈希表里，操作同上20 % 7 = 6，访问array[6]，没有20，返回false。

通过上面的例子可以发现有一些数据被存放到同一个位置了。有些Hash的位置中可能会存放多个元素，这种两个不同的输入值，根据同一散列函数计算出的散列值相同的现象叫做碰撞。

1.2碰撞的处理方法

1.2.1开放定址法

开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到并将记录存入。

在这里插入图片描述

如上，存7,8,9的时候找到null的位置存储，这样并不会引起存储混乱，如果再存储3,5的话，会继续向后找，找到null的位置然后进行存储。ThreadLocal有一个专门存储元素的TheadLocalMap，每次在get 和set元素的时候，会先将目标位置前后的空间搜索一下，将标记为null的位置回收掉，这样大部分不用的位置就收回来了。

1.2.2链地址法

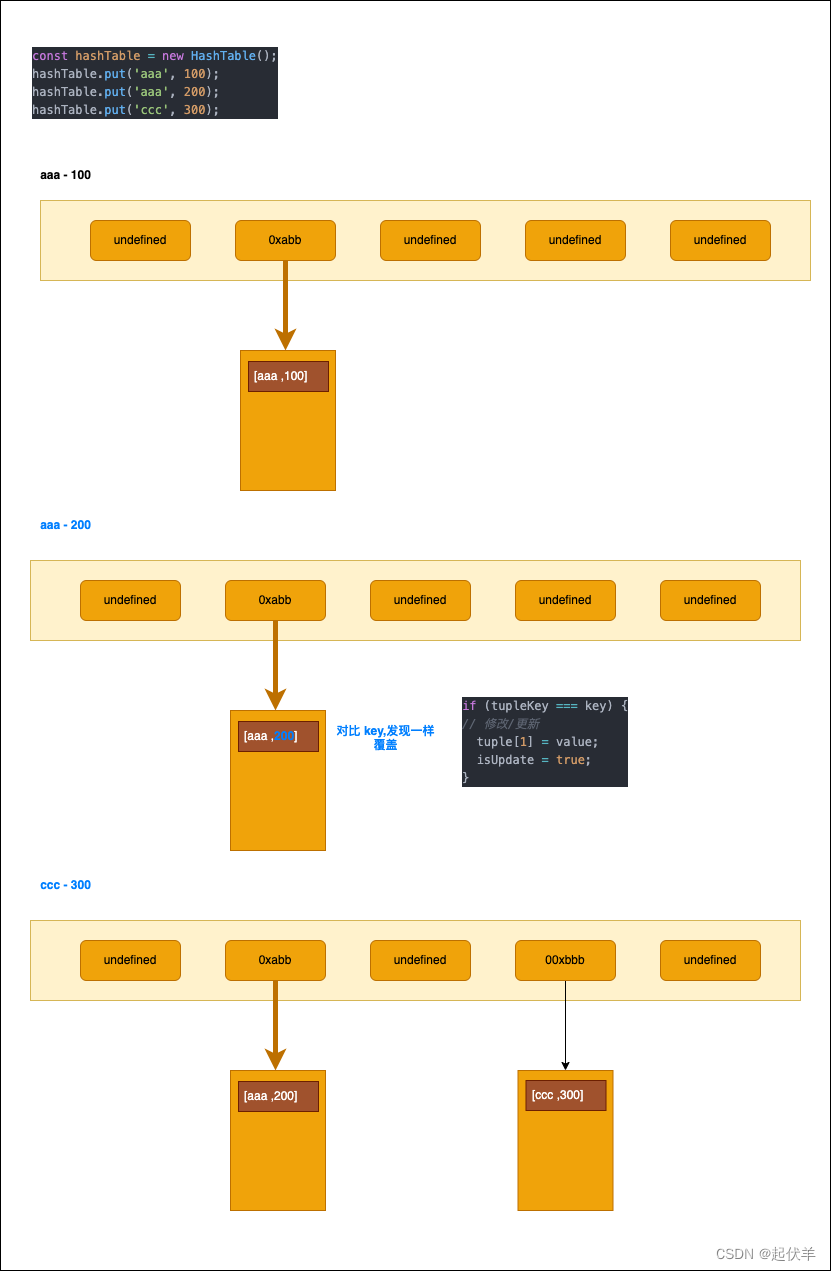
将哈希表的每个单元作为链表的头结点，所有哈希地址为i的元素构成一个同义词链表。即发生冲突时就把该关键字链在以该单元为头结点的链表的尾部。

在这里插入图片描述

1.3HashMap的扩容机制

HashMap的默认容量为16，默认的负载因子为0.75，当HashMap中元素个数超过容量乘以负载因子的个数时，就创建一个大小为前一次两倍的新数组，再将原来数组中的数据复制到新数组中。当数组长度到达64且链表长度大于8时，链表转为红黑树。

那么问题来了，为什么数组长度达到64且链表长度大于8时，转为红黑树？

每次遍历一个链表，平均查找的时间复杂度是 O(n)，n 是链表的长度。红黑树有和链表不一样的查找性能，由于红黑树有自平衡的特点，可以防止不平衡情况的发生，所以可以始终将查找的时间复杂度控制在 O(log(n))。
最初链表还不是很长，所以可能O(n)和 O(log(n)）的区别不大，但是如果链表越来越长，那么这种区别便会有所体现。所以为了提升查找性能，需要把链表转化为红黑树的形式。

那么又有问题了，既然红黑树这么好用，为什么不直接使用红黑树呢？

源码里是这样解释的：

Because TreeNodes are about twice the size of regular nodes,
use them only when bins contain enough nodes to warrant use
(see TREEIFY_THRESHOLD). And when they become too small (due 
removal or resizing) they are converted back to plain bins.

我们可以这样理解，在最开始使用链表的时候，空间占用较少，由于链表比较短，查询时间也较短，随着链表越来越长，需要用红黑树的形式来保证查询的效率。系统里将链表转换成红黑树的阈值设置为8，是因为在理想情况下，链表长度符合泊松分布，各个长度的命中概率依次递减，当长度为8的时候，概率仅为0.00000006。这是一个小于千万分之一的概率，在时间情况中我们的Map里面是不会存储这么多的数据的，所以通常情况下，并不会发生从链表向红黑树的转换。当链表长度降到6的时候就自动转换回链表。

2.队列

2.1队列的概念和基本特征

队列(Queue)：具有一定操作约束的线性表。其只能在**一端插入（入队列，AddQ），而在另一端删除(出队列，DeleteQ)。特征是先进先出(FIFO)**。

队列的顺序存储实现：队列的顺序存储结构通常由一个一维数组和一个记录队列头元素位置的变量**front以及一个记录队列尾元素位置的变量rear**组成
顺环队列使用额外标记Size或tag来判断是否已满，求余函数
队列的链式存储实现：队列的链式存储结构也可以用一个**单链表**实现。插入和删除操作分别在链表的两头进行。rear指向队尾节点，front指向队头结点。

这里看一下基于链表的队列实现。只需要在rear后插入元素，在front删除元素即可。

class ListQueue{
	constructor() {		
		this.size = 0;
		this.front = new ListNode(0);
		this.rear = new ListNode(0);
	}
}

class ListNode {
	constructor(data, next) {		
		this.data = (data === undefined ? 0 : data);
		this.next = (next === undefined ? null : next);
	}
}

/**
 * 入队
 * @param {number} val
 * */

ListQueue.prototype.push(val) {
	const newNode = new ListNode(val);
	let temp = this.front;
	while (temp.next) {
		temp = temp.next;
	}
	temp.next = newNode;
	this.rear = newNode;
	this.size++;
}

/**
 * 出队
 * @return {number}
 * */
ListQueue.prototype.pull() {
	if (this.front.next === null) {
		console.log("队列已空")
	}
	let firstNode = this.front.next;
	this.front.next = firstNode.next;
	this.size--;
	return firstNode.data;
}

/**
 * 遍历队列
 * @return {void}
 **/
ListQueue.prototype.traverse(){
	let temp = this.front.next;
	while (temp) {
		console.log(temp.data + "\t");
		temp = temp.next;
	}
}