跳表原理

跳表是Redis有序集合ZSet底层的数据结构

首先有一个头结点 这个头结点里面的数据是null 就是他就是这个链表的最小值 就算是Math.Min也比它大

 然后我们新建一个节点的时候是怎么操作的呢 先根据参数(假如说是5)创建一个节点 然后把它放在对应位置 就是找到小于他的最大节点 然后把它放在这个小于他的最大节点后面 我们当前只有一个null节点 而且它是最小的 所以直接放在他后面就行了

 然后我们开始提高它的"高度" 这个层数最小为1 剩下的我们用抛硬币的方式决定 如果为正面就加一层 如果背面就不加(当然计算机底层肯定不是抛硬币 是随机算法实现的) 

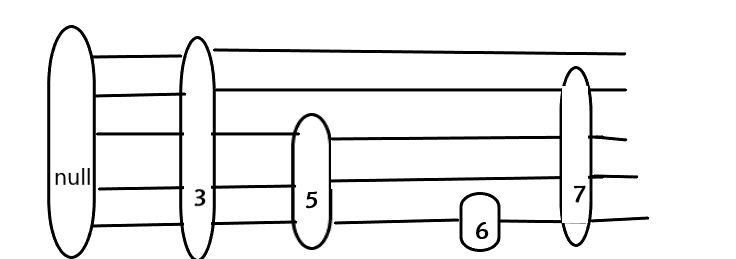
假如说我们在决定五的层数的时候 两次判定都是正面 那他的高度就是3

三层就是三条路 这个路是用来连接下一个节点的(就跟链表似的 只不过链表只有一条路)一会你就知道为啥了 

然后呢 这个null的高度 永远要和最高的节点的高度是一致的 他刚开始是0 现在要变成3 

 然后我们还想加一个6节点 找到比它小的最大节点 是5 那就插在5后面

然后我们随机它的高度 假如说高度是1

哎 看懂没 这个6的高度是1 那么5的上面两条路就连不到它了 直接干后面去了

再来一个高度为5的3节点

比三小的最大节点就是null

所以

 哎 记得null节点要同步

再插一个7节点

查找节点

假如说查找节点6

先从null的最上层出发 找到3 3<6 还得往右走 再往右走空了

所以3往下走一个 再往右走 走到7 7>6 那还得在3往下走一层

3 走到了 5 5<6 那就停在这一层 5再往右走是7 7>6 不行 

5再往下走 不行

5再往下走 找到了6

总结一下 查找一个节点 就是能往右走就往右走 往走走不了就往下走 再往右走

它的时间复杂度为O(logN)  最差复杂度为O(N)

Redis中的跳表

Redis中的跳表相较于经典跳表

1.有重复值

2.最底层有回退指针

3.随机高度+1的概率是百分之25

4.有最大层数限制 Redis 5.0是64层，在Redis 7.0是32层

QS

1.跳表是什么，和普通的链表有什么区别？

跳表算是特殊的链表 他比链表的层数高 可以实现log(N)的查找效率

2.跳表插入数据会影响其它节点层高吗?

就会影响第一个null节点