线性回归
线性回归:根据数据,确定两种或两种以上变量间相互依赖的定量关系
函数表达式:
y
=
f
(
x
1
,
x
2
.
.
.
x
n
)
y = f(x_1,x_2...x_n)
y=f(x1,x2...xn)
回归根据变量数分为一元回归[
y
=
f
(
x
)
y=f(x)
y=f(x)]和多元回归[
y
=
f
(
x
1
,
x
2
.
.
.
x
n
)
y = f(x_1,x_2...x_n)
y=f(x1,x2...xn)],根据函数关系分为线性回归[
y
=
a
x
+
b
y=ax+b
y=ax+b]与非线性回归[
y
=
a
x
2
+
b
x
+
c
y=ax^2+bx+c
y=ax2+bx+c]
平方误差成本函数:
m
i
n
i
m
i
z
e
(
J
)
minimize(J)
minimize(J)
J
=
1
2
m
∑
i
=
1
m
(
y
i
‘
−
y
i
)
2
=
1
2
m
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
2
=
g
(
a
,
b
)
J=\frac{1}{2m} \sum_{i=1}^{m}(y^{`}_i-y_i)^2=\frac{1}{2m} \sum_{i=1}^{m}(ax_i+b-y_i)^2=g(a,b)
J=2m1i=1∑m(yi‘−yi)2=2m1i=1∑m(axi+b−yi)2=g(a,b)
梯度下降算法:
J
=
f
(
p
)
J=f(p)
J=f(p)
p
=
p
−
α
∂
∂
p
i
f
(
p
i
)
p = p - \alpha \frac{\partial}{\partial p_i}f(p_i)
p=p−α∂pi∂f(pi)
寻找极小值的一种方法。通过向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索,直到在极小点收敛。
实验:
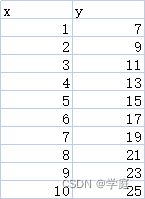
基于generated_data.csv数据,建立线性回归模型,预测x=3.5对应的y值,评估模型表现
#load the data
import pandas as pd
data = pd.read_csv('D:\workspace\data\ML\generated_data.csv')
data.head()
print(type(data), data.shape)
x = data.loc[:,'x']
y = data.loc[:,'y']
print(x,y)
#visualize the data
from matplotlib import pyplot as plt
plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.show()
# set up a linear regression model
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
import numpy as np
x = np.array(x)
x = x.reshape(-1,1)
y = np.array(y)
y = y.reshape(-1,1)
lr_model.fit(x,y)
y_predict = lr_model.predict(x)
print(y_predict)
print(y)
y_predict_single = lr_model.predict([[3.5]])
print(y_predict_single)
# a/b print
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)
from sklearn.metrics import mean_squared_error, r2_score
MSE = mean_squared_error(y, y_predict)
R2 = r2_score(y, y_predict)
print(MSE, R2)
plt.figure()
plt.plot(y,y_predict)
plt.show()
运行结果:
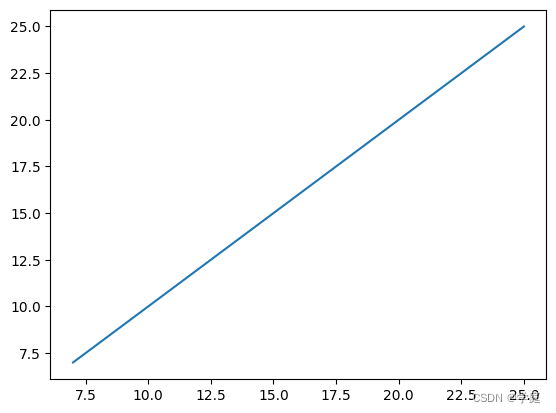
其中MSE为 3.1554436208840474 e − 31 3.1554436208840474e^{-31} 3.1554436208840474e−31,R2为1.0
实验结论:在这个实验中,我们建立了一个单因子线性回归模型,得到x=3.5对应的y值为12,其均方误差(MSE)非常接近于零,而确定系数(R^2)接近于1。这表明我们的模型可以非常好地拟合数据,预测能力非常强。
附:generated_data,csv数据