题目

给你两个整数，被除数 dividend 和除数 divisor。将两数相除，要求 不使用 乘法、除法和取余运算。

整数除法应该向零截断，也就是截去（truncate）其小数部分。例如，8.345 将被截断为 8 ，-2.7335 将被截断至 -2 。

返回被除数 dividend 除以除数 divisor 得到的 商 。

注意：假设我们的环境只能存储 32 位 有符号整数，其数值范围是 [−231,  231 − 1] 。本题中，如果商 严格大于 231 − 1 ，则返回 231 − 1 ；如果商 严格小于 -231 ，则返回 -231 。

示例 1:

输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = 3.33333.. ，向零截断后得到 3 。

示例 2:

输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = -2.33333.. ，向零截断后得到 -2 。

提示：

• -231 <= dividend, divisor <= 231 - 1
• divisor != 0

---

思路 

这道题我是将除法转化为减法，如：

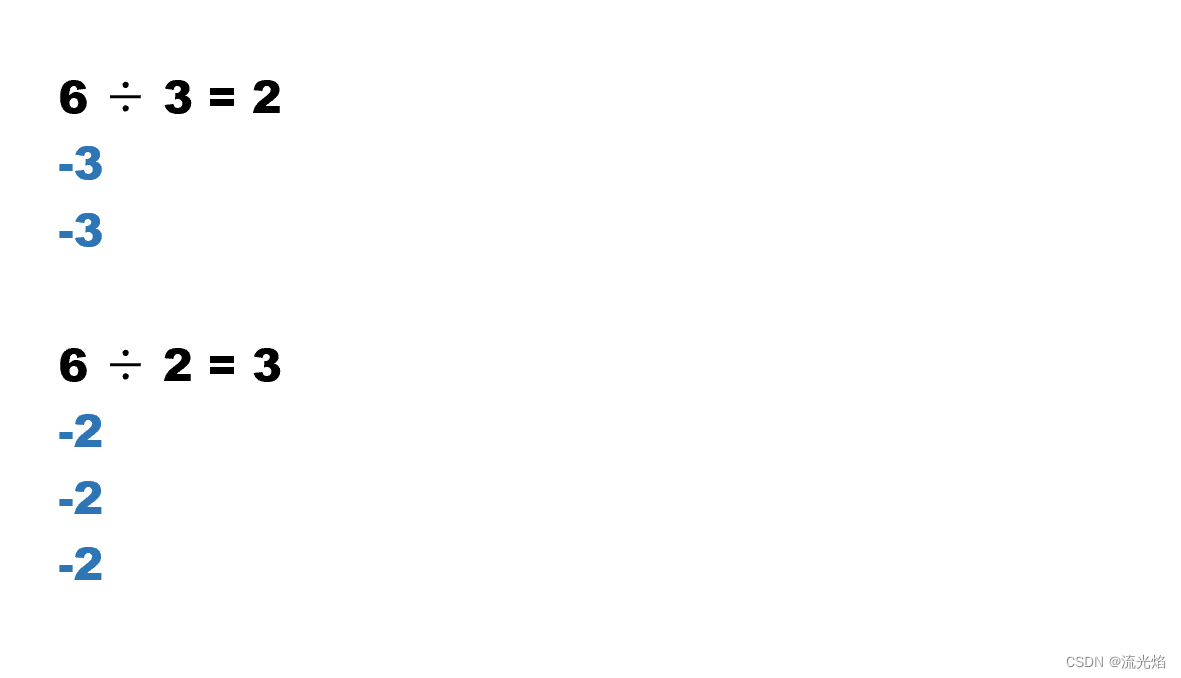
将被除数分为 n 个除数。

这样要求我们先对结果的正负进行判断，然后对除数与被除数取绝对值进行减法。

为了加快速度，令 d= 除数 b ，将 d 每次与被除数 a/2 比较后乘以2，再进行比较，用 c 代表此时的d = c * b

代码

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int divide(int dividend, int divisor);

int main()
{
    int a = 2147483647;
    int b = 1;
    int c = divide(a, b);
    printf("%d", c);
}

int divide(int dividend, int divisor)
{
    int res = 0;
    int sign = 1;
    if ((dividend < 0 && divisor > 0) || (dividend > 0 && divisor < 0))
        sign = -1;
    if (divisor == INT_MIN)
    {
        if (dividend == INT_MIN)
            return 1;
        else
            return 0;
    }
    if (dividend == INT_MIN)
    {
        if (divisor == 1)
            return INT_MIN;
        else if (divisor == -1)
            return INT_MAX;
        res++;
        dividend = dividend + fabs(divisor);
    }
    int a = fabs(dividend);
    int b = fabs(divisor);
    while (a >= b)
    {
        int c = 1;
        int d = b;
        while (a/2 >= d)// a/2 是为了防止 2*d >INT_MAX 同时 a >= 2*d，为后面做准备
        {
            d = 2 * d;
            c = 2 * c;
        }
        a = a - d;//c 指 d 代表 c 个 b
        res = res + c;
    }
    if (sign == -1)
        res = -res;
    return res;
}