文章目录

周赛357
- [2810. 故障键盘](https://leetcode.cn/problems/faulty-keyboard/)
- - 模拟
  - 双端队列O(n)
- [2811. 判断是否能拆分数组](https://leetcode.cn/problems/check-if-it-is-possible-to-split-array/)
- - 脑经急转弯
- [2812. 找出最安全路径](https://leetcode.cn/problems/find-the-safest-path-in-a-grid/)
- - 多源BFS + 倒序枚举 + 并查集
- [2813. 子序列最大优雅度](https://leetcode.cn/problems/maximum-elegance-of-a-k-length-subsequence/)
- - 反悔贪心

周赛357

2810. 故障键盘

难度简单0

你的笔记本键盘存在故障，每当你在上面输入字符 'i' 时，它会反转你所写的字符串。而输入其他字符则可以正常工作。

给你一个下标从 0 开始的字符串 s ，请你用故障键盘依次输入每个字符。

返回最终笔记本屏幕上输出的字符串。

示例 1：

输入：s = "string"
输出："rtsng"
解释：
输入第 1 个字符后，屏幕上的文本是："s" 。
输入第 2 个字符后，屏幕上的文本是："st" 。
输入第 3 个字符后，屏幕上的文本是："str" 。
因为第 4 个字符是 'i' ，屏幕上的文本被反转，变成 "rts" 。
输入第 5 个字符后，屏幕上的文本是："rtsn" 。
输入第 6 个字符后，屏幕上的文本是： "rtsng" 。
因此，返回 "rtsng" 。

示例 2：

输入：s = "poiinter"
输出："ponter"
解释：
输入第 1 个字符后，屏幕上的文本是："p" 。
输入第 2 个字符后，屏幕上的文本是："po" 。
因为第 3 个字符是 'i' ，屏幕上的文本被反转，变成 "op" 。
因为第 4 个字符是 'i' ，屏幕上的文本被反转，变成 "po" 。
输入第 5 个字符后，屏幕上的文本是："pon" 。
输入第 6 个字符后，屏幕上的文本是："pont" 。
输入第 7 个字符后，屏幕上的文本是："ponte" 。
输入第 8 个字符后，屏幕上的文本是："ponter" 。
因此，返回 "ponter" 。

提示：

1 <= s.length <= 100
s 由小写英文字母组成
s[0] != 'i'

模拟

class Solution {
    public String finalString(String s) {
        StringBuilder sb = new StringBuilder();
        for(char c : s.toCharArray()){
            if(c != 'i') sb.append(c);
            else{
                sb.reverse();
            }
        }
        return sb.toString();
    }
}

双端队列O(n)

把反转看成是后续往字符串的头部添加字符。

这可以用双端队列实现。

class Solution {
    public String finalString(String s) {
        Deque<Character> dq = new ArrayDeque<>();
        boolean tail = true; // 填入尾部还是头部
        for(char c : s.toCharArray()){
            if(c == 'i') tail = !tail;
            else if(tail) dq.addLast(c);
            else dq.addFirst(c);
        }
        StringBuilder sb = new StringBuilder();
        for(char c : dq) sb.append(c);
        if(!tail) sb.reverse();
        return sb.toString();
    }
}

2811. 判断是否能拆分数组

难度中等3

给你一个长度为 n 的数组 nums 和一个整数 m 。请你判断能否执行一系列操作，将数组拆分成 n 个非空数组。

在每一步操作中，你可以选择一个 长度至少为 2 的现有数组（之前步骤的结果）并将其拆分成 2 个子数组，而得到的每个子数组，至少需要满足以下条件之一：

子数组的长度为 1 ，或者
子数组元素之和 大于或等于 m 。

如果你可以将给定数组拆分成 n 个满足要求的数组，返回 true ；否则，返回 false 。

**注意：**子数组是数组中的一个连续非空元素序列。

示例 1：

输入：nums = [2, 2, 1], m = 4
输出：true
解释：
第 1 步，将数组 nums 拆分成 [2, 2] 和 [1] 。
第 2 步，将数组 [2, 2] 拆分成 [2] 和 [2] 。
因此，答案为 true 。

示例 2：

输入：nums = [2, 1, 3], m = 5 
输出：false
解释：
存在两种不同的拆分方法：
第 1 种，将数组 nums 拆分成 [2, 1] 和 [3] 。
第 2 种，将数组 nums 拆分成 [2] 和 [1, 3] 。
然而，这两种方法都不满足题意。因此，答案为 false 。

示例 3：

输入：nums = [2, 3, 3, 2, 3], m = 6
输出：true
解释：
第 1 步，将数组 nums 拆分成 [2, 3, 3, 2] 和 [3] 。
第 2 步，将数组 [2, 3, 3, 2] 拆分成 [2, 3, 3] 和 [2] 。
第 3 步，将数组 [2, 3, 3] 拆分成 [2] 和 [3, 3] 。
第 4 步，将数组 [3, 3] 拆分成 [3] 和 [3] 。
因此，答案为 true 。

提示：

1 <= n == nums.length <= 100
1 <= nums[i] <= 100
1 <= m <= 200

脑经急转弯

看样例3

class Solution {
    public boolean canSplitArray(List<Integer> nums, int m) {
        if(nums.size() <= 2) return true;
        for(int i = 1; i < nums.size(); i++){
            if(nums.get(i) + nums.get(i-1) >= m) return true;
        }
        return false;
    }
}

2812. 找出最安全路径

难度中等10

给你一个下标从 0 开始、大小为 n x n 的二维矩阵 grid ，其中 (r, c) 表示：

如果 grid[r][c] = 1 ，则表示一个存在小偷的单元格
如果 grid[r][c] = 0 ，则表示一个空单元格

你最开始位于单元格 (0, 0) 。在一步移动中，你可以移动到矩阵中的任一相邻单元格，包括存在小偷的单元格。

矩阵中路径的 安全系数 定义为：从路径中任一单元格到矩阵中任一小偷所在单元格的最小曼哈顿距离。

返回所有通向单元格 (n - 1, n - 1) 的路径中的 最大安全系数 。

单元格 (r, c) 的某个相邻单元格，是指在矩阵中存在的 (r, c + 1)、(r, c - 1)、(r + 1, c) 和 (r - 1, c) 之一。

两个单元格 (a, b) 和 (x, y) 之间的 曼哈顿距离 等于 | a - x | + | b - y | ，其中 |val| 表示 val 的绝对值。

示例 1：

输入：grid = [[1,0,0],[0,0,0],[0,0,1]]
输出：0
解释：从 (0, 0) 到 (n - 1, n - 1) 的每条路径都经过存在小偷的单元格 (0, 0) 和 (n - 1, n - 1) 。

示例 2：

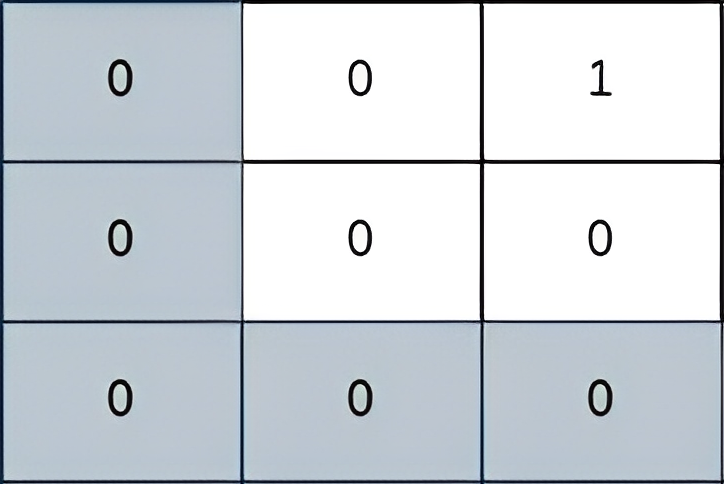
输入：grid = [[0,0,1],[0,0,0],[0,0,0]]
输出：2
解释：
上图所示路径的安全系数为 2：
- 该路径上距离小偷所在单元格（0，2）最近的单元格是（0，0）。它们之间的曼哈顿距离为 | 0 - 0 | + | 0 - 2 | = 2 。
可以证明，不存在安全系数更高的其他路径。

示例 3：

输入：grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
输出：2
解释：
上图所示路径的安全系数为 2：
- 该路径上距离小偷所在单元格（0，3）最近的单元格是（1，2）。它们之间的曼哈顿距离为 | 0 - 1 | + | 3 - 2 | = 2 。
- 该路径上距离小偷所在单元格（3，0）最近的单元格是（3，2）。它们之间的曼哈顿距离为 | 3 - 3 | + | 0 - 2 | = 2 。
可以证明，不存在安全系数更高的其他路径。

提示：

1 <= grid.length == n <= 400
grid[i].length == n
grid[i][j] 为 0 或 1
grid 至少存在一个小偷

多源BFS + 倒序枚举 + 并查集

第三题主站出过好几次了，1631，1970，2258都是这个套路，这次这个和这些里前两个比较像，那就是二分猜答案，dijkstra，并查集三种做法(二分猜答案的确是有点卡常). 还有778和2577

class Solution {
    private final static int[][] dirts = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    public int maximumSafenessFactor(List<List<Integer>> grid) {
        int n = grid.size();
        // 1. 从所有1出发，写一个多源BFS，计算出每个格子(i, j)到最近的 1 的曼哈顿距离dis[i][j]
        List<int[]> q = new ArrayList<>();
        int[][] dis = new int[n][n];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                if(grid.get(i).get(j) > 0)
                    q.add(new int[]{i, j});
                else dis[i][j] = -1;
            }   
        }
        // 将坐标按每个距离从小到大进行分组，后面倒序枚举答案时需要合并对应分组
        List<List<int[]>> groups = new ArrayList<>();
        groups.add(q);
        while(!q.isEmpty()){ // 多源BFS
            List<int[]> tmp = q;
            q = new ArrayList<>();
            for(int[] p : tmp){
                for(int[] d : dirts){
                    int x = p[0] + d[0], y = p[1] + d[1];
                    if(0 <= x && x < n && 0 <= y && y < n && dis[x][y] < 0){
                        q.add(new int[]{x, y});
                        dis[x][y] = groups.size();
                    }
                }
            }
            groups.add(q); // 相同 dis 分组记录
        }

        // 并查集
        fa = new int[n * n];
        for(int i = 0; i < n * n; i++)
            fa[i] = i;
        // 由于多源BFS时最后会添加上一个空的list，因此答案从倒数第二个开始枚举
        for(int ans = groups.size() - 2; ans > 0; ans--){
            // 1. 合并分组  2. 判断
            List<int[]> g = groups.get(ans);
            for(int[] p : g){ // 枚举分组中的点，将其与四个方向上距离远的点合并
                int i = p[0], j = p[1];
                for(int[] d : dirts){
                    int x = i + d[0], y = j + d[1];
                    // dis[x][y] >= dis[i][j] 说明 相邻的点已经加入并查集中
                    if(0 <= x && x < n && 0 <= y && y < n && dis[x][y] >= dis[i][j]){
                        fa[find(x * n + y)] = find(i * n + j);
                        // fa[find(i * n + j)] = find(x * n + y); 也可以
                    }
                }
            }
            if(find(0) == find(n * n - 1)) return ans;
        }
        return 0;
    }

    // 并查集模板
    private int[] fa;

    private int find(int x) {
        if (fa[x] != x) fa[x] = find(fa[x]);
        return fa[x];
    }
}

2813. 子序列最大优雅度

难度困难6

给你一个长度为 n 的二维整数数组 items 和一个整数 k 。

items[i] = [profiti, categoryi]，其中 profiti 和 categoryi 分别表示第 i 个项目的利润和类别。

现定义 items 的 子序列 的 优雅度 可以用 total_profit + distinct_categories2 计算，其中 total_profit 是子序列中所有项目的利润总和，distinct_categories 是所选子序列所含的所有类别中不同类别的数量。

你的任务是从 items 所有长度为 k 的子序列中，找出 最大优雅度 。

用整数形式表示并返回 items 中所有长度恰好为 k 的子序列的最大优雅度。

**注意：**数组的子序列是经由原数组删除一些元素（可能不删除）而产生的新数组，且删除不改变其余元素相对顺序。

示例 1：

输入：items = [[3,2],[5,1],[10,1]], k = 2
输出：17
解释：
在这个例子中，我们需要选出长度为 2 的子序列。
其中一种方案是 items[0] = [3,2] 和 items[2] = [10,1] 。
子序列的总利润为 3 + 10 = 13 ，子序列包含 2 种不同类别 [2,1] 。
因此，优雅度为 13 + 22 = 17 ，可以证明 17 是可以获得的最大优雅度。

示例 2：

输入：items = [[3,1],[3,1],[2,2],[5,3]], k = 3
输出：19
解释：
在这个例子中，我们需要选出长度为 3 的子序列。 
其中一种方案是 items[0] = [3,1] ，items[2] = [2,2] 和 items[3] = [5,3] 。
子序列的总利润为 3 + 2 + 5 = 10 ，子序列包含 3 种不同类别 [1, 2, 3] 。 
因此，优雅度为 10 + 32 = 19 ，可以证明 19 是可以获得的最大优雅度。

示例 3：

输入：items = [[1,1],[2,1],[3,1]], k = 3
输出：7
解释：
在这个例子中，我们需要选出长度为 3 的子序列。
我们需要选中所有项目。
子序列的总利润为 1 + 2 + 3 = 6，子序列包含 1 种不同类别 [1] 。
因此，最大优雅度为 6 + 12 = 7 。

提示：

1 <= items.length == n <= 105
items[i].length == 2
items[i][0] == profiti
items[i][1] == categoryi
1 <= profiti <= 109
1 <= categoryi <= n
1 <= k <= n

反悔贪心

题解：https://leetcode.cn/problems/maximum-elegance-of-a-k-length-subsequence/solution/fan-hui-tan-xin-pythonjavacgo-by-endless-v2w1/

先按profit从大到小排序，再获取profit最大的前k项，

后续的项(n-k)如果要提升整体值，唯有通过增加category数目来优化。

class Solution {
    /*
    找到一个 base, 先选最大的 k 个利润，这可能是一个答案
    
    考虑下一个项目要不要选
    由于利润从大到小排序，利润和 total profit 不会变大
    所以重点就在 distinct_categories 能不能变大? (考虑变化量)

    分类讨论:
    1. 如果新添加的项目的类别之前选过了，那么 distinct_categories 不会变大
    2. 如果新添加的项目的类别之前没选过（没出现过）
    2.1 如果移除的项目的类别只有一个，那么 distinct_categories-1+1，不变，不行
    2.2 如果移除的项目的类别有多个，那么 distinct_categories+1，这种情况就是可以的
        - 选一个利润最小的移除，用一个栈维护
    */
    public long findMaximumElegance(int[][] items, int k) {
        Arrays.sort(items, (a, b) -> b[0] - a[0]); // 按利润从大到小排序
        long ans = 0, totalProfit = 0;
        Set<Integer> vis = new HashSet<>();
        Deque<Integer> duplicate = new ArrayDeque<>(); // 重复类别的利润
        for(int i = 0; i < items.length; i++){
            int profit = items[i][0], category = items[i][1];
            if(i < k){
                totalProfit += profit;
                if(!vis.add(category)) // 重复类别
                    duplicate.push(profit);
            }else if(!duplicate.isEmpty() && vis.add(category)){
                totalProfit += profit - duplicate.pop(); // 选一个重复类别中的最小利润替换
            }// else：比前面的利润小，而且类别还重复了，
            //      选它只会让 totalProfit 变小，vis.size() 不变，优雅度不会变大
            ans = Math.max(ans, totalProfit + (long)vis.size() * vis.size());
        }
        return ans;
    }
}