文章目录
- 一、stack的使用
- 1.stack的介绍
- 2.stack的使用
- 二、queue的使用
- 1.queue的护额晒
- 2.queue的使用
- 三、stack和queue相关算法题
- 1.最小栈
- 2.栈的压入、弹出序列
- 3.逆波兰表达式
- 4.两个栈实现一个队列
- 5.用两个队列实现栈
- 6.二叉树的层序遍历
- 1.双队列
- 2.用一个变量levelSize去控制
- 7.二叉树的层序遍历Ⅱ
一、stack的使用
1.stack的介绍

栈是一种容器适配器,专门设计用于在 LIFO 上下文中操作(后进先出),其中元素只从容器的一端插入和提取。
栈被实现为容器适配器,这些类使用特定容器类的封装对象作为其底层容器,提供一组特定的成员函数来访问其元素。 元素从特定容器的“后端”被推入/弹出,这被称为栈的顶部。
底层容器可以是任何标准的容器类模板,也可以是其他一些专门设计的容器类。容器应该支持以下操作:empty、size、back、push_back、pop_front
标准容器类 vector、deque 和 list 满足这些要求。默认情况下,如果没有为特定的堆栈类实例化指定容器类,则使用标准容器 deque。
这里我们需要知道的是,Container适配器就是一个现有的容器进行的一个转换
也就是说,适配器的本质就是一种复用
2.stack的使用
我们先看stack的接口有哪些
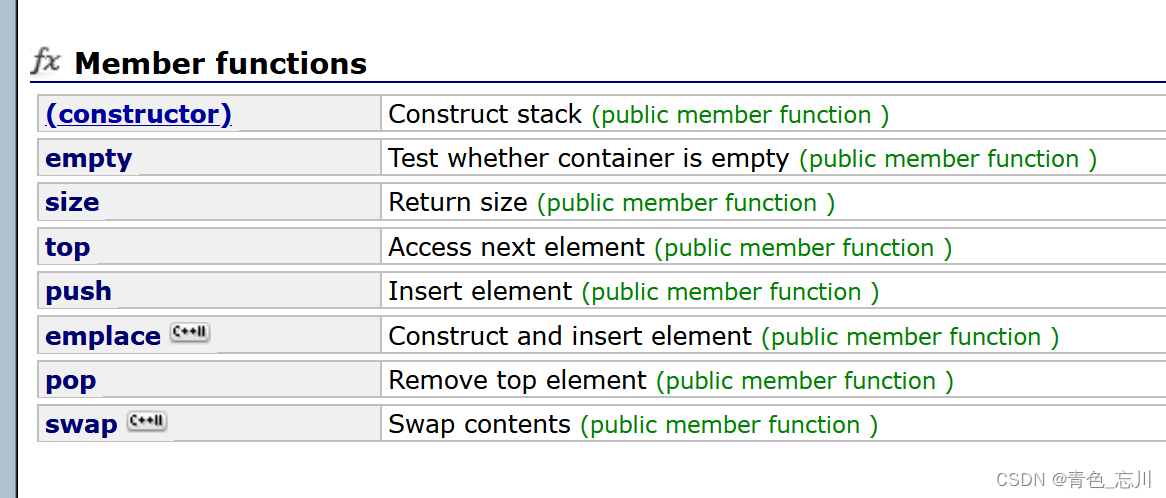
如上所示,这里其实我们一看就已经猜出了七七八八了。因为与前面是string、vector、list是十分相似的。只要结合它的先进先出的特性,我们就知道每个函数都是什么意思了。
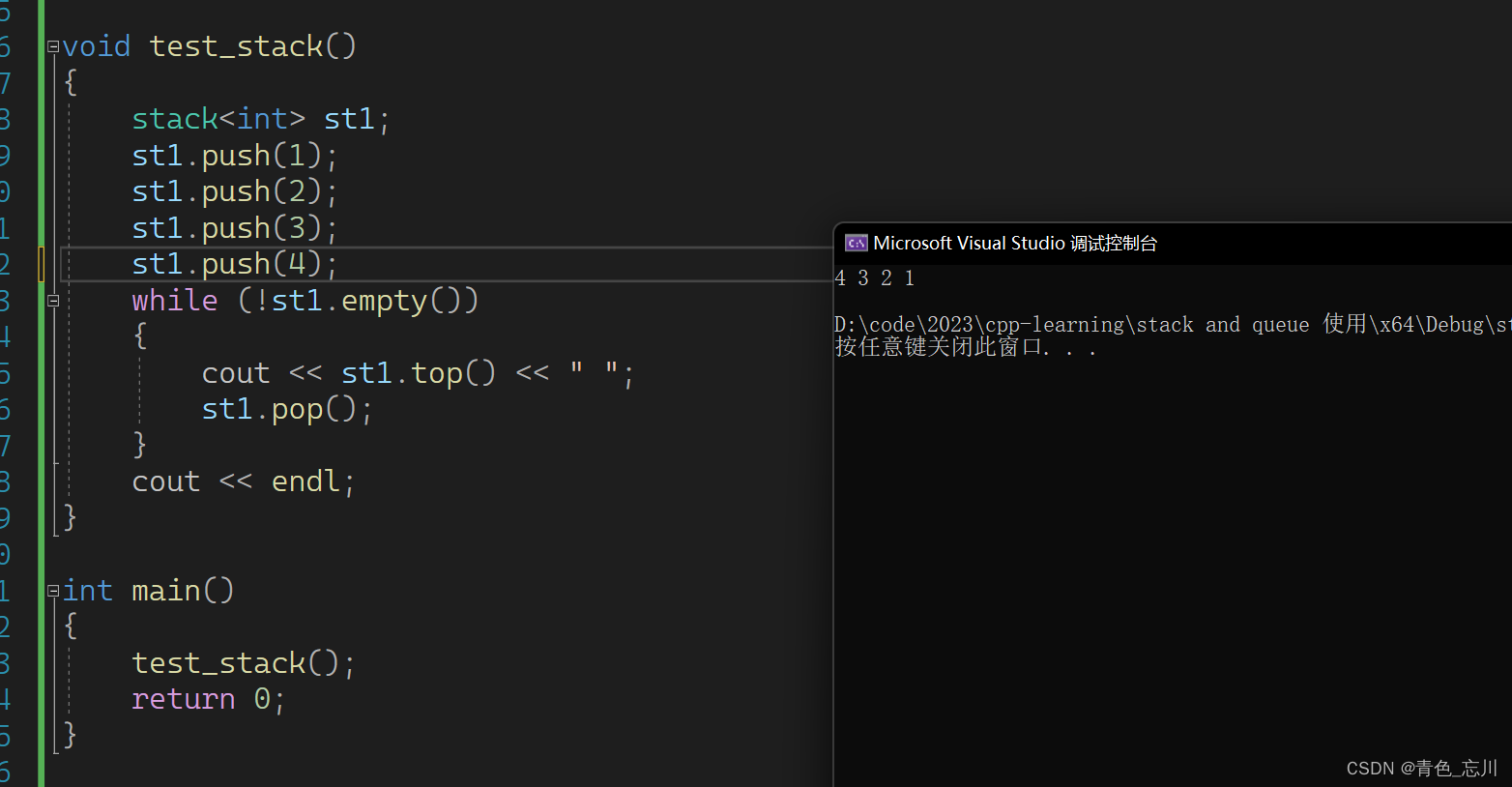
对于stack的使用是非常简单的
void test_stack()
{
stack<int> st1;
st1.push(1);
st1.push(2);
st1.push(3);
st1.push(4);
while (!st1.empty())
{
cout << st1.top() << " ";
st1.pop();
}
cout << endl;
}
二、queue的使用
1.queue的护额晒

队列是一种容器适配器,专门设计用于在FIFO上下文中操作(先进先出),其中将元素插入容器的一端并从另一端提取。
队列是作为容器适配器实现的,容器适配器是使用特定容器类的封装对象作为其底层容器的类,提供一组特定的成员函数来访问其元素。元素被推入特定容器的“后面”,并从其“前面”弹出。
底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:empty、size、front、back、push_back、pop_back。
标准容器类deque和list满足这些要求。默认情况下,如果没有为特定队列类实例化指定容器类,则使用标准容器队列。
2.queue的使用
同样的,我们先来看queue的接口有哪些

在这些接口中,和stack是类似的,只要我们知道了queue的特性是先进先出。我们就能很轻松的推测出每个接口的意思
对于queue的使用是很简单的
void test_queue()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}

三、stack和queue相关算法题
1.最小栈
题目链接:最小栈
题目解析:在这道题中,我们为了模拟这种情况,我们可以在成员变量中定义两个栈,一个栈作为正常的出入数据使用,一个栈用来存储最小值。
首先是构造函数,由于我们的成员变量都是自定义类型,所以会自动调用他们的默认构造函数,即他们也会走初始化列表,所以默认构造函数我们是可以直接不用管的。甚至于我们可以直接删掉题目给的构造函数,因为我们不写,编译器自己生成一个。
其次我们的大逻辑是这样的,当我们最小栈为空的时候,我们的最小栈是需要入一个数据的,当我们将要插入的元素是小于等于最小栈要插入的元素的时候,我们会将这个元素给入最小栈
当我们pop的时候,我们也是同理的,如果我们要删除的数据等于最小栈的栈顶元素,那么就也要删除最小栈的栈顶元素。
class MinStack {
public:
MinStack()
{}
void push(int val) {
st.push(val);
if(min.empty()||(val<=min.top()))
{
min.push(val);
}
}
void pop() {
int val=st.top();
st.pop();
if(val==min.top())
{
min.pop();
}
}
int top() {
return st.top();
}
int getMin() {
return min.top();
}
private:
stack<int> st;
stack<int> min;
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
2.栈的压入、弹出序列
题目链接:栈的压入弹出序列
题目解析:我们可以使用一个栈来模拟它的入栈出栈逻辑,只要顺着它的思路最终我们的这个栈是空栈的话,那么就说明是匹配的,否则不匹配
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
// write code here
stack<int> st;
int n=pushV.size();
int j=0;
for(int i=0;i<n;i++)
{
st.push(pushV[i]);
while(!st.empty() && st.top()==popV[j])
{
st.pop();
j++;
}
}
return st.empty();
}
};
3.逆波兰表达式
题目链接:逆波兰表达式
再谈这道题之前,我们应该先知道什么是逆波兰表达式,我们正常的都是中缀表达式,即3+2*5这种的,都被称之为中缀表达式。
而中缀表达式在计算机中是很难进行运算的。我们需要先将其转换为后缀表达式,前文所说的中缀表达式转化为后缀表达式后应该为3 2 5 * +。后缀表达式的特点就是操作数的顺序不变,而操作符的顺序按照优先级进行了重排。
我们先来看一下后缀运算符是如何进行运算的:
- 操作数入栈
- 如果是操作符,取出栈顶的两个元素进行计算,计算结果放入栈中
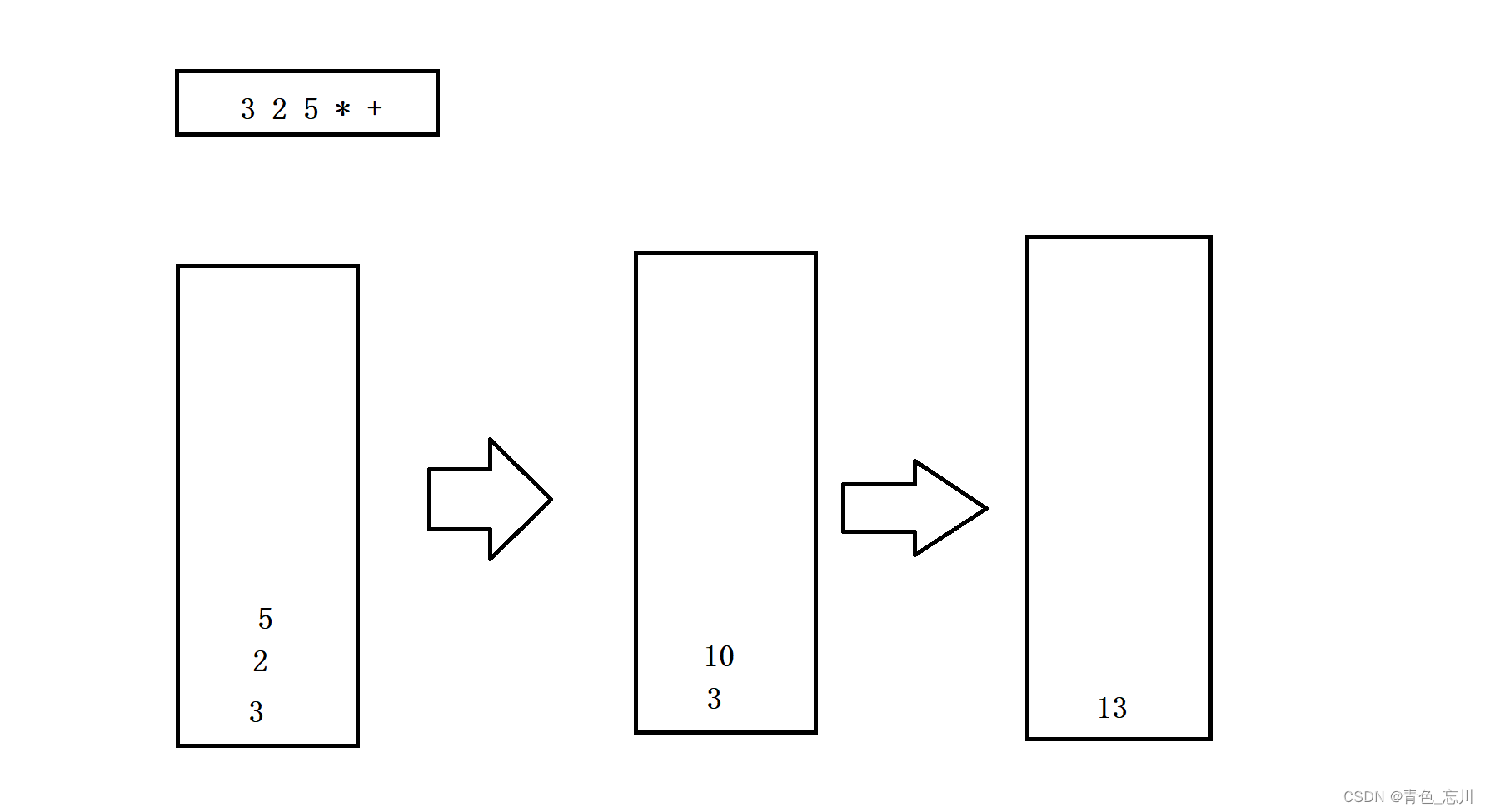
那么如何使得中缀转为后缀呢?
- 操作数输出(即将操作数放到一个容器中)
- 操作符入栈 : ①栈为空,当前操作符比栈顶的优先级高,继续入栈 ②栈不为空,且当前操作符比栈顶的优先级低或者相等,则输出栈顶操作符(因为运算符的优先级只与它相邻的操作符有关,是相对的,如果后面出现了一个更高的操作符,我们无法确定后面是否还有更高的操作符,反而是如果有一个相对较低的操作符,那么前两个肯定是可以进行运算的)
- 表达式结束后,依次出栈顶的操作符
- 注意,有可能会在转换的中间出现连续出操作符的情况,即栈里面已经存储了好几个运算符了,下面的一个运算符要比好几个都要低,就要连续出好几个运算符
比如说2+4-1*3,这个中缀表达式,按照上面的规则可以化为
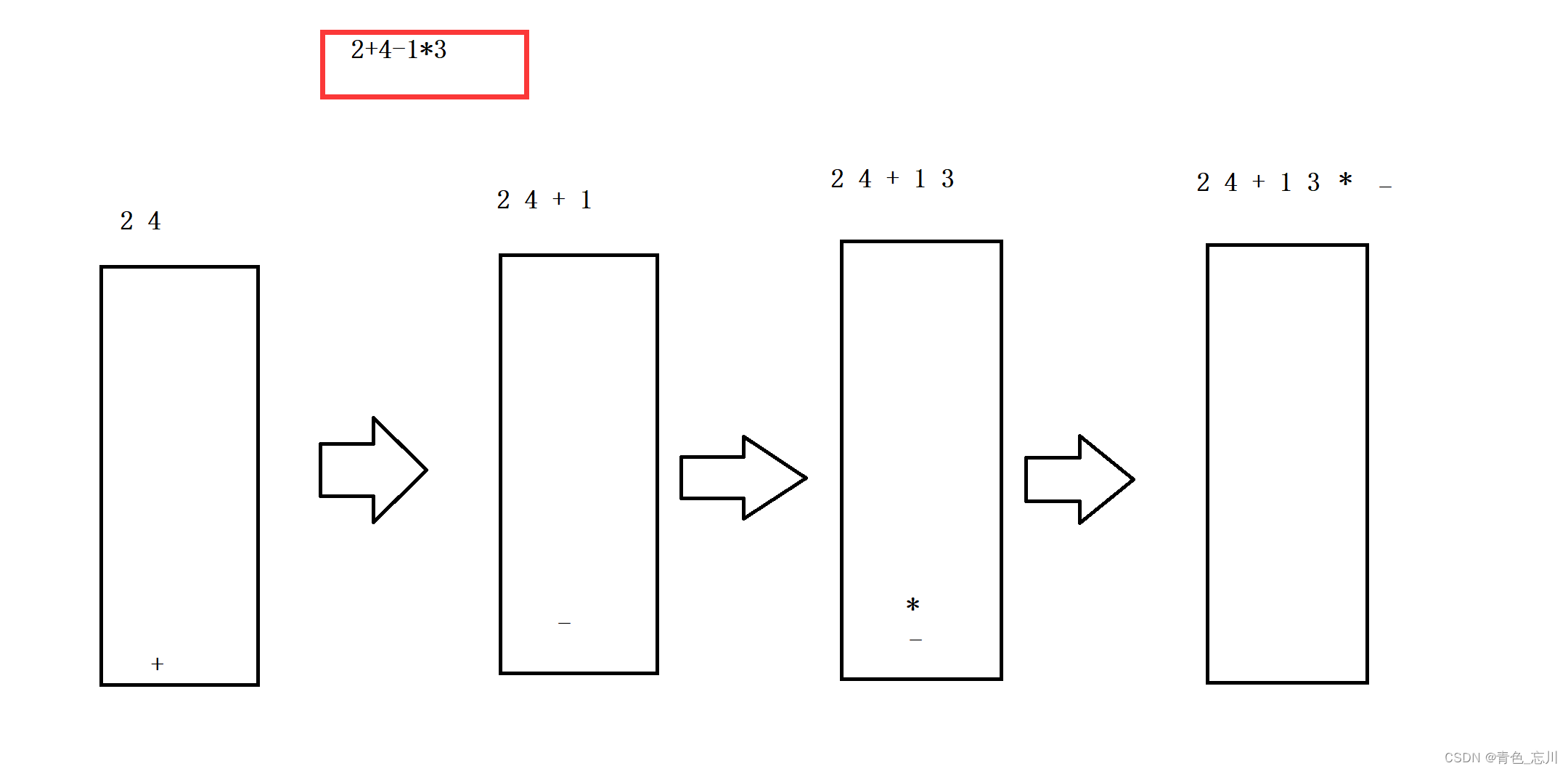
上面都是正常情况的下的处理,但是还有时候会出现括号的影响。
这里可以考虑加上一个特殊标记,当我们这个标记生效时,就代表进入括号内了。或者在这里走一个递归也是可以的。递归的方法就是在遇到括号的时候,我们将括号里面的运算符就需要放入一个新的栈中了。相当于我们只需要让括号返回一个结果就可以了。但是数据还是输出在原来的顺序表中的
我们在回过头来看这道题,我们有了上面的分析,就很容易写出下面代码了。
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto& str : tokens)
{
if(str=="+"||str=="-"||str=="*"||str=="/")
{
int right=st.top();
st.pop();
int left=st.top();
st.pop();
switch(str[0])
{
case '+':st.push(left+right);break;
case '-':st.push(left-right);break;
case '*':st.push(left*right);break;
case '/':st.push(left/right);break;
}
}
else
{
st.push(stoi(str));
}
}
return st.top();
}
};
4.两个栈实现一个队列
题目链接:两个栈实现一个队列
对于这个题,我们在之前也已经做过一次分析了,只不过上一次是用C语言手撕了一个栈来实现了。而现在呢,我们有C++的库了,因此我们就可以直接使用C++的库来完成这件事。
class MyQueue {
public:
MyQueue() {}
void push(int x) {
_push.push(x);
}
int pop() {
if(_pop.empty())
{
while(!_push.empty())
{
int val=_push.top();
_push.pop();
_pop.push(val);
}
}
int val=_pop.top();
_pop.pop();
return val;
}
int peek() {
if(_pop.empty())
{
while(!_push.empty())
{
int val=_push.top();
_push.pop();
_pop.push(val);
}
}
return _pop.top();
}
bool empty() {
return (_push.empty()&&_pop.empty());
}
private:
stack<int> _push;
stack<int> _pop;
};
/**
* Your MyQueue object will be instantiated and called as such:
* MyQueue* obj = new MyQueue();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->peek();
* bool param_4 = obj->empty();
*/
5.用两个队列实现栈
题目链接:用两个队列实现栈
这道题与上面的题类似,我们也是曾经使用C语言做过,不过由于C语言没有轮子,就需要我们自己造轮子,有了很多的麻烦。
class MyStack {
public:
MyStack() {}
void push(int x) {
if(q1.empty())
{
q2.push(x);
}
else
{
q1.push(x);
}
}
int pop() {
if(q1.empty())
{
while(q2.size()>1)
{
int val=q2.front();
q2.pop();
q1.push(val);
}
int val=q2.front();
q2.pop();
return val;
}
else
{
while(q1.size()>1)
{
int val=q1.front();
q1.pop();
q2.push(val);
}
int val=q1.front();
q1.pop();
return val;
}
}
int top() {
if(q1.empty())
{
return q2.back();
}
else
{
return q1.back();
}
}
bool empty() {
return (q1.empty()&&q2.empty());
}
private:
queue<int> q1;
queue<int> q2;
};
/**
* Your MyStack object will be instantiated and called as such:
* MyStack* obj = new MyStack();
* obj->push(x);
* int param_2 = obj->pop();
* int param_3 = obj->top();
* bool param_4 = obj->empty();
*/
6.二叉树的层序遍历
题目链接:二叉树的层序遍历
对于这道题,如果不是用C++来完成的话,用C去完成的话是非常难的。不仅我们要确保我们造的轮子是正确的,而且还有很多细节需要进行处理,但我们如果使用C++的话可以极大的简化很多操作
1.双队列
我们可以使用两个队列去完成这件事,一个队列用来存储结点指针,一个队列用来存储该节点处于哪个层。这样我们就可以知道哪个结点是那个层的了,自然我们就很容易的得知层序遍历了。
2.用一个变量levelSize去控制
这种思路是比较奇妙的,我们使用一个变量来确定当前该层有多少个结点,用一个队列来存储结点,然后就是层序遍历的基本套路,每出一个结点,带来两个孩子。将每一层的数据存储在一个vector中,然后一层结束后将这一层的vector插入到vector<vector<int>>中。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
int levelSize=0;
if(root)
{
q.push(root);
levelSize=1;
}
vector<vector<int>> vv;
while(!q.empty())
{
vector<int> v;
for(int i=0;i<levelSize;i++)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
levelSize=q.size();
}
return vv;
}
};
7.二叉树的层序遍历Ⅱ
题目链接:二叉树的层序遍历Ⅱ
对于这道题目,我们可以注意到他是让倒着遍历的。和前一道题基本是一样的,只是改变了vv的顺序。即相当于将vv给逆序。那么这道题就太简单了,直接将前面这道题给拷贝过来,然后调用库里面的reverse即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
queue<TreeNode*> q;
int levelSize=0;
if(root)
{
q.push(root);
levelSize=1;
}
vector<vector<int>> vv;
while(!q.empty())
{
vector<int> v;
for(int i=0;i<levelSize;i++)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
levelSize=q.size();
}
reverse(vv.begin(),vv.end());
return vv;
}
};
好了,本期内容就到这里了
如果对你有帮助的话,不要忘记点赞加收藏哦!!!