概述

主成分分析（Principal Component Analysis）是一种常见的数据分析方式，常用于高维数据的降维，提取数据的主要特征分量，其数学推导可以从最大可分性和最近重构性两个角度着手，前者的优化条件为划分后方差最大，后者的优化条件为点到划分平面距离最小，此处将从最大可分性的角度进行证明。

前置知识——线性代数

向量表示和基变换

内积

假设有如下两个向量， $A=[a_1,a_2,..,a_n]$ 和 $B=[b_1,b_2,..,b_n]$ ，那么两个向量的内积为 $\begin{align*} AB^T &= [a_1,a_2,..,a_n]*[b_1,b_2,..,b_n]^T \\ &= a_1b_1+a_2b_2+...+a_nb_n \\ &= |A||B|cos\theta \end{align*}$
其中 $\theta=\frac{\vec{A}\cdot \vec{B}}{|A||B|}$
其几何表示为
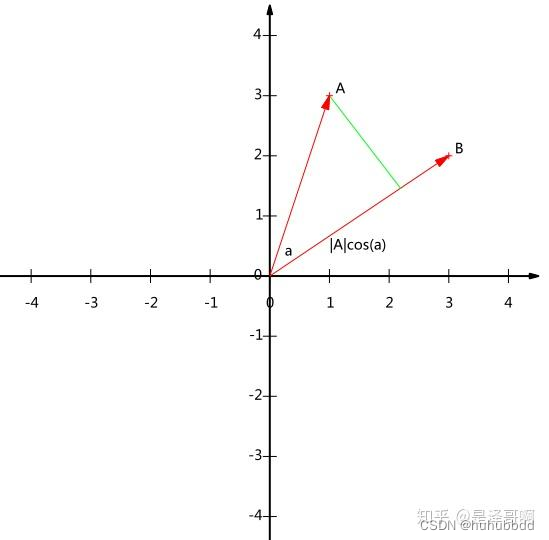- 由此，我们可以看出A 与 B 的内积等于 A 到 B 的投影长度乘以 B 的模，当B为单位向量时，则 $A\cdot B=|A|cos\theta$ 此时，A 与 B 的内积值等于 A 向 B 所在直线投影的标量大小。

基变换

我们常说的平面直角坐标系，实际上是由 $(1, 0), (0, 1)$ 这组基确定的一个二维向量空间，例如向量 $A = (3, 2)$ 实际是指一个在 x 轴投影为 3 ,而 y 轴的投影为 2的向量。
对于 $A = (3, 2)$ 来说，如果我们想求它在 $(1, 0), (0, 1)$ 这组基下的坐标的话，分别内积即可，我们可以用矩阵乘法来简洁的表示这一过程 $\begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 3 & 2\\ %第一行元素 \end{array} \right) %右括号 \end{equation*}\cdot \begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 1 & 0\\ %第一行元素 0 & 1 \\ %第二行元素 \end{array} \right) %右括号 \end{equation*}=\begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 3 & 2\\ %第一行元素 \end{array} \right) %右括号 \end{equation*}$
此处将 $(3, 2)$ 与 $(1, 0), (0, 1)$ 做内积实质上是分别将其投影到两个基上。并且此处的运算结果仍然是 $(3, 2)$ ，这是因为 $(1, 0), (0, 1)$ 是一组标准的正交基，并且 $(3, 2)$ 本身已经在 $(1, 0), (0, 1)$ 确定的线性空间内，因此做了投影之后得到的向量仍然是它本身。

我们也可以使用标准正交基以外的各种基，但这组基必须是线性无关的。通过类似的矩阵乘法运算，我们可以将左边矩阵的每一个行向量都变换到以右矩阵所有列向量为基的线性空间内，因此一个矩阵可以表示为一种线性变换。
所以，我们大致可以得到一个结论，我们要准确描述向量，首先要确定一组基，然后给出在基所在的各个直线上的投影值。为了方便求坐标，我们希望这组基向量模长为 1。因为向量的内积运算，当模长为 1 时，内积可以直接表示投影。然后还需要这组基是线性无关的，我们一般用正交基，非正交的基也是可以的，不过正交基有较好的性质。

从最大可分性角度证明

上面我们讨论了选择不同的基可以对同样一组数据给出不同的表示，如果基的数量少于向量本身的维数，则可以达到降维的效果。但是我们还没回答一个最关键的问题：如何选择基才是最优的？ 或者说，如果我们有一组 N 维向量，现在要将其降到 K 维 $(K < N)$ ，那么我们应该如何选择 K 个基才能最大程度保留原有的信息？
一种直观的看法是：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解，熵越大所含信息越多。

方差

我们知道数值的分散程度，可以用数学上的方差来表述。在一维空间中，一个变量的方差可以看做是每个元素与变量均值的差的平方和的均值，即： $Var(a)=\frac{1}{m}\sum^{m}_{i=1}{(a_i-\mu)^2}$ 为了方便处理，我们将每个变量的均值都化为 0 ，因此方差可以直接用每个元素的平方和除以元素个数表示： $Var(a)=\frac{1}{m}\sum^{m}_{i=1}{a_i^2}$ 于是上面的问题被形式化表述为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

协方差

在一维空间中我们可以用方差来表示数据的分散程度。而对于高维数据，我们用协方差进行约束，协方差可以表示两个变量的相关性。为了让两个变量尽可能表示更多的原始信息，我们希望它们之间不存在线性相关性，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。
协方差可由如下公式计算 $Cov(a,b)=\frac{1}{m-1}\sum^{m}_{i=1}(a_i-\mu_a)(b_i-\mu_b)$ 为了简单起见，我们仍设置 $\mu_a=\mu_b=0$ ，同时，当样本数较大时，不必在意其是 $m$ 还是 $m - 1$ ，为了方便计算，我们分母取 $m$ ，因此 $Cov(a,b)=\frac{1}{m}\sum^{m}_{i=1}a_ib_i$
当协方差为 0 时，表示两个变量不存在线性相关性（非线性相关性未知，因此不能说两个变量相互独立）。为了让协方差为 0，我们选择第二个基时只能在与第一个基正交的方向上进行选择，因此最终选择的两个方向一定是正交的。
至此，我们得到了降维问题的优化目标：将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。

协方差矩阵

假设我们只有 $a$ 和 $b$ 两个变量，服从均值为 0 的高斯分布，我们将它们按列组成矩阵 $X$ （每一列看作一个变量的不同取值，每个变量我们可以看作是样本的一个特征），那么 $X=\begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列，每一列都居中放置 a_1 & b_1\\ %第一行元素 a_2 & b_2\\ \vdots & \vdots\\ a_n & b_n\\ \end{array} \right) %右括号 \end{equation*}$
然后，我们通过矩阵内积，求得协方差矩阵
$\begin{align*} \frac{1}{m}X^TX &=\begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} \frac{1}{m}\sum^{m}_{i=1}{a_i^2} & \frac{1}{m}\sum^{m}_{i=1}a_ib_i\\ \\ \frac{1}{m}\sum^{m}_{i=1}a_ib_i & \frac{1}{m}\sum^{m}_{i=1}{b_i^2}\\ \end{array} \right) %右括号 \end{equation*} \\ \\ &= \begin{equation*} %开始数学环境 \left( %左括号 \begin{array}{ccc} Cov(a,a) & Cov(a,b) \\ \\ Cov(b,a)& Cov(b,b)\\ \end{array} \right) %右括号 \end{equation*} \\ \end{align*}$
我们可以看到这个矩阵对角线上的分别是两个变量的方差，而其它元素是 a 和 b 的协方差，两者被统一到了一个矩阵里。
我们很容易推广到一般情况：设我们有 m 个 n 维数据记录，将其排列成矩阵 $X_{m,n}$ ，设 $C=\frac{1}{m}X^TX$ ，则 $C$ 是一个对称矩阵，其对角线分别对应各个变量的方差，而第 $i$ 行 $j$ 列和 $j$ 行 $i$ 列元素相同，表示 $i$ 和 $j$ 两个变量的协方差。

矩阵对角化

根据我们的优化条件，我们需要将除对角线外的其它元素化为 0（最小化变量之间的线性相关性），并且将对角线上元素按大小从上到下排列（方便选取前k个方差最大的变量），这样我们就达到了优化目的。
下面，我们进一步探讨原矩阵与其基变换后得到的矩阵它们的协方差矩阵之间的关系
- 设原矩阵为 $X$ ，原矩阵对应的协方差矩阵为 $C$ ， $P$ 为一组基按列组成的矩阵，设 $Y = XP$ ，则 $Y$ 为 $X$ 对 $P$ 做基变换后得到的矩阵，设 $Y$ 的协方差矩阵为 $D$ ，则 $D$ 与 $C$ 之间的关系为 $\begin{align*} D &= \frac{1}{m}Y^TY \\ &= \frac{1}{m}(XP)^T(XP)\\ &= \frac{1}{m}P^TX^TXP\\ &= P^T\frac{1}{m}(X^TX)P\\ &= P^TCP \end{align*}$ 因此，二者协方差矩阵之间的关系就是 $D=P^TCP$
这样我们就看清楚了，我们要找的 $P$ 是能让原始协方差矩阵 $C$ 对角化的 $P$ 。换句话说，优化目标变成了寻找一个矩阵 $P$ ，使得 $D$ 是一个对角矩阵，并且对角元素按从大到小依次排列，那么 $P$ 的前 $K$ 列就是要寻找的基，用 $X$ 乘 $P$ 的前 $K$ 列组成的矩阵就使得 $X$ 从 $N$ 维降到了 $K$ 维。
那么如何寻找到这样的 $P$ 呢？
- 由上文知道，协方差矩阵 $C$ 是一个是对称矩阵，在线性代数中实对称矩阵有一系列非常好的性质，具体来讲，每个实对称矩阵都可以分解成实特征向量和实特征值 $A=Q\Lambda Q^T$ 其中 $Q$ 是 $A$ 的特征向量组成的正交矩阵(正交矩阵的列向量一定是线性无关的)， $\Lambda$ 是对角矩阵，特征值 $\Lambda_{i,i}$ 对应的特征向量是矩阵 $Q$ 的第 $i$ 列，记作 $Q_{:,i}$ ，因为 $Q$ 是正交矩阵，所以 $A$ 可以看作是沿着 $Q_{:,i}$ 方向延展了 $\Lambda_{i,i}$ 倍的空间。
- 因此，一个 $n$ 行 $n$ 列的实对称矩阵一定可以找到 $n$ 个单位正交特征向量，我们将协方差矩阵 $C$ 做特征分解，可以得到
  $C=Q\Lambda Q^T$
  因为Q是正交矩阵，所以有 $Q^{-1}=Q^T$ ，因此上式可化为 $\Lambda=Q^TCQ$
  此时 $\Lambda$ 恰好为一个对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复，因为一个 $r$ 重的特征值对应着 $r$ 个线性无关的特征向量）。
至此，我们就找到了这样的 $P : P = Q$ 。
实现对角元素按从大到小依次排列也很简单，只需要同时将特征值和特征向量从大到小排列即可，则用 $P$ 的前 $K$ 行组成的矩阵便是我们所求的一组基。