前言
二叉树在算法中是经常考察的点,但是要在本地测试的话,就必须自己构建二叉树。在算法题中,一般给我们的都是一个数组,或者是二叉树的形状。因此,需要将数组转换为二叉树,这样才能测试出自己的代码是否符合题意。
构建基础知识
我采用的是完全二叉树的方式进行构建二叉树的,因此需要知道完全二叉树的性质:
对于完全二叉树,若从上至下,从左至右,并从1开始进行编号,规则如下:
编号为 i 的节点
- 其左孩子的编号必为 2*i
- 其右孩子的编号必为 2*i + 1
构建事项
由于我采用的是数组实现,因此与基本的性质有一些差别,这是因为数组的下标是从0开始计算的,从而规则更改为:
编号为 i 的节点
- 其左孩子的编号必为 2 * i + 1
- 其右孩子的编号必为 2 * i + 2
正式构建
构建一般的(int)二叉树
说明:
因为一般的算法题中是以int 数组为代表的考题,因此将其单独提出来
构建二叉树节点
代码实现
public class TreeNode {
// 节点数据
public int val;
// 左节点 遍历
public TreeNode left;
// 右节点
public TreeNode right;
public TreeNode() {
}
public TreeNode(int val) {
this.val = val;
}
}二叉树构建方法
代码实现
public TreeNode intArrayToBTree(int [] arrs) {
// 判空处理,返回空节点
if (arrs == null || arrs.length == 0) {
return new TreeNode();
}
// 创建和数组长度相同的集合
List<TreeNode> nodes = new ArrayList<>(arrs.length);
// 遍历数组,将数组元素转为集合节点
for (int obj : arrs) {
TreeNode treeNode = new TreeNode();
treeNode.val = obj;
nodes.add(treeNode);
}
// 按照完全二叉树的规则构建,数组中的后半部分元素都是叶子节点,它们没有左右子节点。所以循环只需要处理前半部分的非叶子节点即可。
// i < arrs.length/2 - 1 能够将所有左右子节点不为null的元素给遍历出来,剩下最后一个(在左节点上)或者最后两个(在右节点上)
// 保证循环只在前半部分有效的节点范围内进行迭代,避免处理不必要的叶子节点。
for (int i = 0; i < arrs.length/2 - 1; i++) {
TreeNode node = nodes.get(i);
// 首先,由于是通过数组构建的二叉树(数组下标从0开始)
// 其次,由完全二叉树的性质(从1开始计数,左孩子为2i,右孩子为2i +1 ) 再结合 数组下标0 开始计数 可知:
// 树的左节点为 2i +1;树的右节点为:2i +2
node.left = nodes.get(i*2 + 1);
node.right = nodes.get(i*2 + 2);
}
// 只有当总节点数是奇数时,最后一个父节点才有右子节点
int lastPNodeIndex = arrs.length/2 - 1;
TreeNode lastPNode = nodes.get(lastPNodeIndex);
// 左孩子节点
lastPNode.left = nodes.get(lastPNodeIndex*2 + 1);
if (arrs.length%2 != 0) {
lastPNode.right = nodes.get(lastPNodeIndex*2 + 2);
}
return nodes.get(0);
}
测试方法
代码实现
public static void main(String[] args) {
int [] arr = {1,3,2,5,3,9};
TreeNode treeNode = new TreeNode();
TreeNode root = treeNode.intArrayToBTree(arr);
}测试过程
使用Debug模式运行(主要看fori循环那里)
在经过第一次的循环(将数组元素转为节点元素的循环)

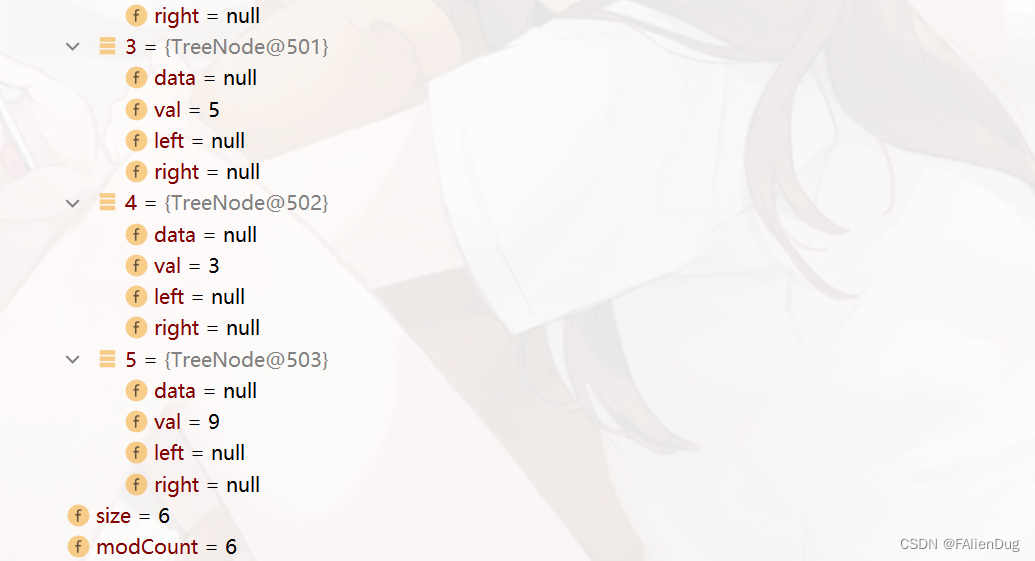
由于QQ长截图失效,将其截图为两张图,其实最主要的是观察第一个节点的变化,之后就直接第一个节点变化的值。
在第二个for循环开始前,需要关注一下循环判断条件
i < arrs.length/2 - 1i < arrs.length/2 - 1 能够将所有左右子节点都不为null的元素给遍历出来,直至叶子节点,剩下最后一个叶子节点(在左节点上)或者最后两个叶子节点(在右节点上)
这个条件是为了保证循环只在前半部分有效的节点范围内进行迭代,避免处理不必要的叶子节点。
进入第一次for循环(i = 0)

经过第一次循环(i = 0),可知根节点为1,其左节点为3(其下还没遍历出左右孩子),其右节点为2(其下还没遍历出左右孩子)
进入第二次for循环(i = 1)
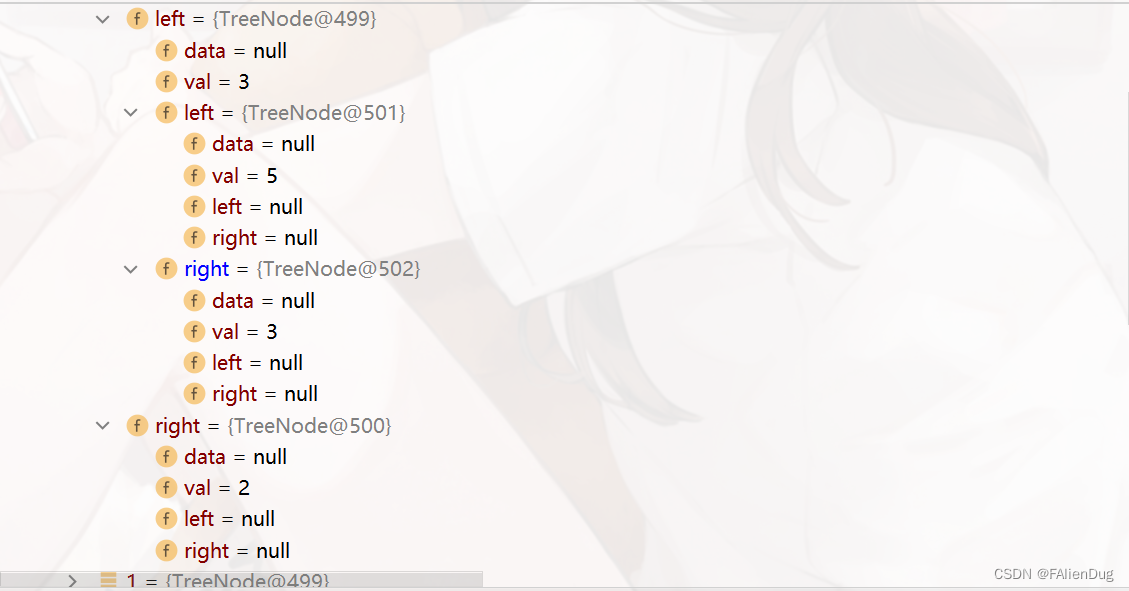
第 二次循环确定了根节点1的左孩子 的 左右孩子的值(也就是在第一次遍历基础上,得到遍历左节点3的左右孩子的值),从结果中可知,根节点的右孩子在这一次循环中没有添加进来,因为默认一次只添加左右孩子两个值,而节点9 是最后一个值,没有满足循环条件,因此右节点没有变化。
当i = 1 结束时,会进行 i++ 操作,操作完成后 i = 2,不满足循环条件, 循环对于最后一个节点9,需要对其进行判断
int lastPNodeIndex = arrs.length/2 - 1;
TreeNode lastPNode = nodes.get(lastPNodeIndex);
// 左孩子节点
lastPNode.left = nodes.get(lastPNodeIndex*2 + 1);
// 只有当总节点数是奇数时,最后一个父节点才有右子节点
if (arrs.length%2 != 0) {
lastPNode.right = nodes.get(lastPNodeIndex*2 + 2);
}
测试结果:
根节点: 1
第一层节点:3 2
第二层节点:5 3 9
构成的完全二叉树:
1
/ \
3 2
/ \ / \
5 3 9 (null)
构建特殊的(Object) 二叉树
有些算法场景也会用到其他类型作为数据域的节点构成的二叉树,因此也在上面基础上将int类的的数据节点改为Object类型的数据节点,其实现方法大同小异。
构建二叉树节点
public class TreeNode {
// 节点数据
public Object data;
// 左节点 遍历
public TreeNode left;
// 右节点
public TreeNode right;
public TreeNode() {
}
public TreeNode(Object data) {
this.data = data;
}
public TreeNode(Object data, TreeNode left, TreeNode right) {
this.data = data;
this.left = left;
this.right = right;
}
}二叉树构建方法
/**
* 数组遍历构成二叉树
* @param arrs 数组
* @return 二叉树根节点
*/
public TreeNode arrayToBTree(Object[] arrs) {
if (arrs == null || arrs.length == 0) {
return new TreeNode();
}
List<TreeNode> nodes = new ArrayList<>(arrs.length);
for (Object obj : arrs) {
TreeNode treeNode = new TreeNode();
treeNode.data = obj;
nodes.add(treeNode);
}
for (int i = 0; i < arrs.length/2 - 1; i++) {
TreeNode node = nodes.get(i);
node.left = nodes.get(i*2 + 1);
node.right = nodes.get(i*2 + 2);
}
// 只有当总节点数是奇数时,最后一个父节点才有右子节点
int lastPNodeIndex = arrs.length/2 - 1;
TreeNode lastPNode = nodes.get(lastPNodeIndex);
lastPNode.left = nodes.get(lastPNodeIndex*2 + 1);
if (arrs.length%2 != 0) {
lastPNode.right = nodes.get(lastPNodeIndex*2 + 2);
}
return nodes.get(0);
}