1.根据二叉树创建字符串 力扣
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。
来源:力扣(LeetCode)
class Solution {
public:
string tree2str(TreeNode* root)
{
//根据前序遍历确定字符串
if(root==nullptr)
return "";
string tree=to_string(root->val);
//只有左右子树都为空不保留括号,其他情况都保留括号
if(root->left||root->right)
{
tree+='(';
tree+=tree2str(root->left);
tree+=')';
}
if(root->right)
{
tree+='(';
tree+=tree2str(root->right);
tree+=')';
}
return tree;
}
};2.二叉树分层遍历 力扣
给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1]
输出:[[1]]示例 3:
输入:root = []
输出:[]来源:力扣(LeetCode)
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
//用队列来确定
queue<TreeNode*> TreeNode1;
vector<vector<int>> vv;
int levesize=0;
if(root)
{
TreeNode1.push(root);
levesize=1;
}
while(!TreeNode1.empty())
{
vector<int> v;
for(int i=0;i<levesize;i++)
{
TreeNode* front= TreeNode1.front();
TreeNode1.pop();
v.push_back(front->val);
if(front->left)
{
TreeNode1.push(front->left);
}
if(front->right)
{
TreeNode1.push(front->right);
}
}
vv.push_back(v);
//TreeNode.pop();
levesize=TreeNode1.size();
}
return vv;
}
};3.二叉树的最近公共祖先 力扣
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1来源:力扣(LeetCode)
class Solution {
public:
bool find_node(TreeNode* root, TreeNode* p, stack<TreeNode*>& path)
{
if(root==nullptr)
return false;
path.push(root);
if (root == p)
return true;
if( find_node(root->left, p, path))
return true;
if( find_node(root->right, p, path))
return true;
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
//使用两个栈存放二叉树要找的数据,
stack<TreeNode*> ppath;
stack<TreeNode*> qpath;
find_node(root, p, ppath);
find_node(root, q, qpath);
//确定长度
while (ppath.size() > qpath.size())
{
ppath.pop();
}
while (ppath.size() < qpath.size())
{
qpath.pop();
}
while (ppath.size() == qpath.size())
{
if (ppath.top() == qpath.top())
{
return ppath.top();
}
ppath.pop();
qpath.pop();
}
return nullptr;
}
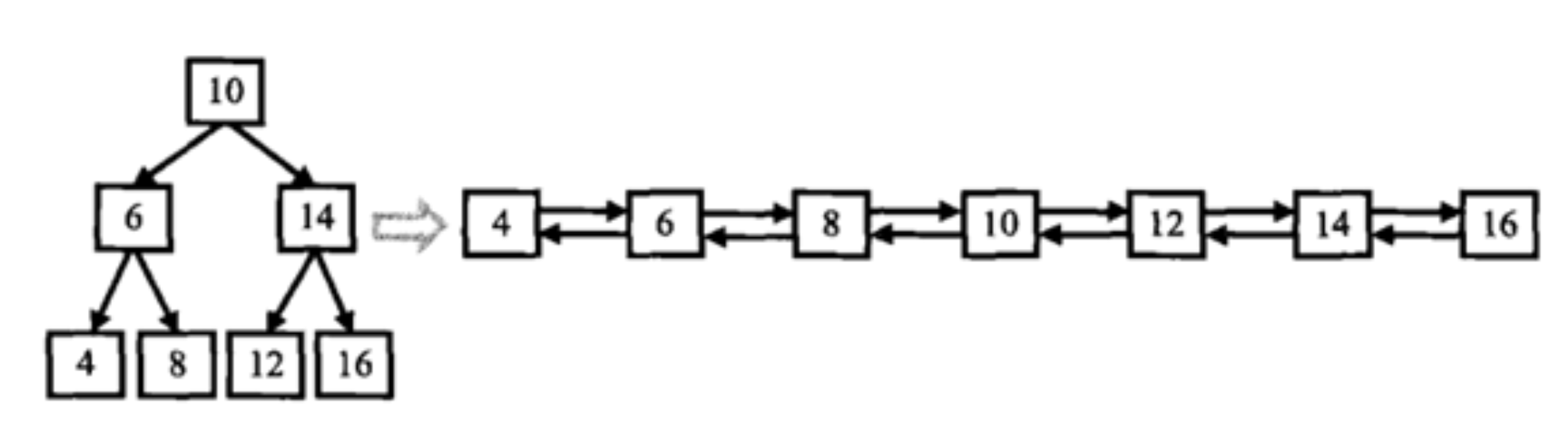
};4. 二叉搜索树与双向链表_牛客题霸_牛客网
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
数据范围:输入二叉树的节点数 0≤n≤10000≤n≤1000,二叉树中每个节点的值 0≤val≤10000≤val≤1000
要求:空间复杂度O(1)O(1)(即在原树上操作),时间复杂度 O(n)O(n)注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构4.你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:
二叉树的根节点
返回值描述:
双向链表的其中一个头节点。
示例1
输入:
{10,6,14,4,8,12,16}返回值:From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;
class Solution {
void Indor(TreeNode* cur,TreeNode*& prev)
{
//确定双向链表
if(cur==nullptr)
return;
Indor(cur->left,prev);
cur->left=prev;
if(prev)
prev->right=cur;
prev=cur;
Indor(cur->right,prev);
}
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* prev=nullptr;
Indor(pRootOfTree,prev);
//判断头结点
TreeNode* head=pRootOfTree;
while(head&&head->left)
{
head=head->left;
}
return head;
}
};
5.从前序与中序确定二叉树 力扣
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]来源:力扣(LeetCode)
class Solution {
TreeNode* buildTree(vector<int>& preorder,vector<int>& inorder,int& prie,
int inbegin,int inend)
{
if(inbegin>inend)//结束条件
return nullptr;
TreeNode* root=new TreeNode(preorder[prie]);
int rooti=inbegin;
while(rooti<=inend)
{
if(preorder[prie]==inorder[rooti])
break;
rooti++;
}
++prie;
root->left=buildTree(preorder,inorder,prie,inbegin,rooti-1);
root->right=buildTree(preorder,inorder,prie,rooti+1,inend);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int i=0;
TreeNode* root=buildTree(preorder,inorder,i,0,inorder.size()-1);
return root;
}
};6.中序与后序确定二叉树 力扣
class Solution {
TreeNode* _buildTree(vector<int>& inorder,vector<int>& postorder,
int& n,int inbegin,int inend)
{
if(inbegin>inend)
return nullptr;
TreeNode* root=new TreeNode(postorder[n]);
int rooti=inbegin;
while(rooti<=inend)
{
if(postorder[n]==inorder[rooti])
break;
rooti++;
}
n--;
root->right=_buildTree(inorder,postorder,n,rooti+1,inend);//先右再左
root->left=_buildTree(inorder,postorder,n,inbegin,rooti-1);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
int n=postorder.size()-1;
return _buildTree(inorder,postorder,n,0,postorder.size()-1);
}
};7.二叉树后序遍历迭代算法 力扣
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[3,2,1]来源:力扣(LeetCode)
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
stack<TreeNode*> st;
vector<int> nums;
TreeNode* cur=root;
TreeNode* prev=nullptr;
while(cur||!st.empty())
{
while(cur)
{
st.push(cur);
cur=cur->left;
}
TreeNode* top=st.top();
if(top->right==nullptr||top->right==prev)//防止重复遍历
{
prev=top;
st.pop();
nums.push_back(top->val);
}
else
{
cur=top->right;
}
}
return nums;
}
};