PBR Material
草履虫都能看懂的PBR讲解(迫真)
先前看了很多遍类似的了,结合《Unity Shader 入门精要》中的内容整理了下便于以后理解,以后有补充再添加。
光与材质相交会发生散射和吸收,散射改变光的方向,吸收改变光的能量。
在均匀介质中,光沿直线传播。传播过程中材质的折射率变化,光的传播方向也会发生变化,介质边界折射率突变,光会发生散射现象。
实际光和物体交互非常复杂,光沿直线传播也只是一种特例。介质的表面是不平滑的,由很多的微表面构成,微表面折射的光被折射到物体内部,一部分被物体吸收,一部分被重新散射到物体外部。对于金属材质,折射的光往往会被立刻吸收,对于非金属材质,折射到物体外部的光又被称为次表面散射光。

渲染建模中,会考虑两个介质的边界无限大且光学平滑。在此前提下,光在不同介质边界会被划分为两个方向:散射和折射。
双向反射分布函数BRDF
一般用辐射率去量化光。辐射率L是单位面积,单位方向上的光源辐射通量。评估光线的颜色和亮度。
计算光线与物体交互后的出射辐射率,需要使用BRDF计算。
当光线随着入射方向I到达表面某点时, BRDF=f(I,V) 表示了有多少能量被反射到了观察方向V上。
观察方向上的某个点出射辐射率等于所有入射辐射率叠加运算的结果。
由此引出反射等式:
L 0 = ∫ Ω f ( I , v ) ∗ L i ( I ) ∗ ( n ⋅ I ) d ω i L_0=\int_{\Omega}f(I,v)*L_i(I)*(n \cdot I)d\omega_i L0=∫Ωf(I,v)∗Li(I)∗(n⋅I)dωi
BRDF表示了入射光线在观察方向上的权重分布。(n.I)表示f(I,v)*Li在材质表面的投影结果。渲染过程中采用的是精确的光源,方向确定,大小无限小。可以简化反射等式为:
L 0 = π f ( I , v ) ∗ c l i g h t ∗ ( n ⋅ I ) L_0=\pi f(I,v)*c_{light}*(n \cdot I) L0=πf(I,v)∗clight∗(n⋅I)
BRDF决定了着色是否基于物理,需要满足交换律和能量守恒定律。基于这些理论,BRDF可以用于描述表面反射和次表面散射。其中表面反射被成为高光反射项,次表面散射被称为漫反射项。
漫反射
最简单的Lambert 模型中Lambertian BRDF表示为:
f L a m b s t ( I , v ) = c d i f f u s e / π f_{Lambst}(I,v)=c_{diffuse}/\pi fLambst(I,v)=cdiffuse/π
假定漫反射在任何方向的强度相同。满足能量守恒定律的BRDF要求反射能量不能超过入射能量,BRDF在半球内积分为1,所以要除Pi。(具体要好好思考下,关于能量守恒定律这点,书上有公式能很好的解释这点,就不多复述了)。
对于给定入射光方向的出射漫反射辐射::
L d i f f = c d i f f u s e / π ∗ L i ( I ) ∗ ( n ⋅ I ) L_{diff}=c_{diffuse}/\pi *L_i(I)*(n\cdot I) Ldiff=cdiffuse/π∗Li(I)∗(n⋅I)
一点补充:

高光反射
微面源理论提出,物体表面是由很多人眼看不到的微面元组成的。微面元可以被认为是光学平滑的。
发生反射时,不同的微表面会把光线反射到不同方向,只有一部分为微面反射的光能够进入我们的眼睛,即表面。下图介绍了可能出现的反射情况。
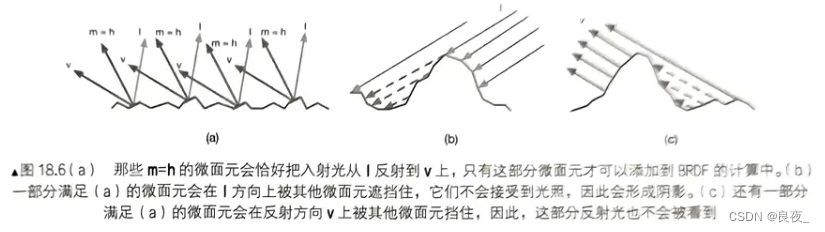
h为I和v的半角矢向量,m为表面法线。
法线分布函数NDF可以用于计算有多少比例的微面元满足m=h, 阴影遮掩函数G(I,v,h) 用于计算满足m=h的微面元中有多少因为遮挡不被看到,给出了活跃微面元的所占浓度,活跃的微面元才能把光线反射到观察方向上。
Blinn模型中的法线分布函数是最简单的,而Unity中standard shader使用了GGX模型。
D b l i n n ( h ) = ( n ⋅ h ) g l o s s D_{blinn}(h)=(n\cdot h)^{gloss} Dblinn(h)=(n⋅h)gloss
D G G X ( h ) = α 2 π ( α 2 − 1 ) ( n ⋅ h ) 2 + 1 D_{GGX}(h)=\cfrac{\alpha^2}{\pi(\alpha^2-1)(n\cdot h)_2+1 } DGGX(h)=π(α2−1)(n⋅h)2+1α2
其中α=roughness^2。
阴影掩盖函数使用了GGX衍生的Smith-Schlick模型。
G ( I , v , h ) = 1 ( ( n ⋅ 1 ) ( 1 − k ) + k ) ( ( n ⋅ v ) ( 1 − k ) + k ) G(I,v,h)=\cfrac{1}{((n\cdot 1)(1-k)+k)((n\cdot v)(1-k)+k) } G(I,v,h)=((n⋅1)(1−k)+k)((n⋅v)(1−k)+k)1
其中k=roughness^2/2。
菲涅尔反射函数可以计算活跃的微面元会把多少光反射到观察方向上,表示了反射光线占入射光想的比例。
F ( I , h ) = F 0 + ( 1 − F 0 ) ( 1 − 1 ⋅ h ) 5 F(I,h)=F_0+(1-F_0)(1-1\cdot h)^{5} F(I,h)=F0+(1−F0)(1−1⋅h)5
其中F0为高光反射系数,可以理解为高光反射颜色。常常会受到材质金属性的影响。
float3 F0 = float3(0.04, 0.04, 0.04);
F0 = lerp(F0, ALBEDO(input.UV), metallic);