本文分享一个Filerpy的说明文档和代码示例文档,有关于 Python 中的卡尔曼和贝叶斯滤波器。该方法可以应用于气象遥感等领域。
说明文档:https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html
参考代码链接:https://nbviewer.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb
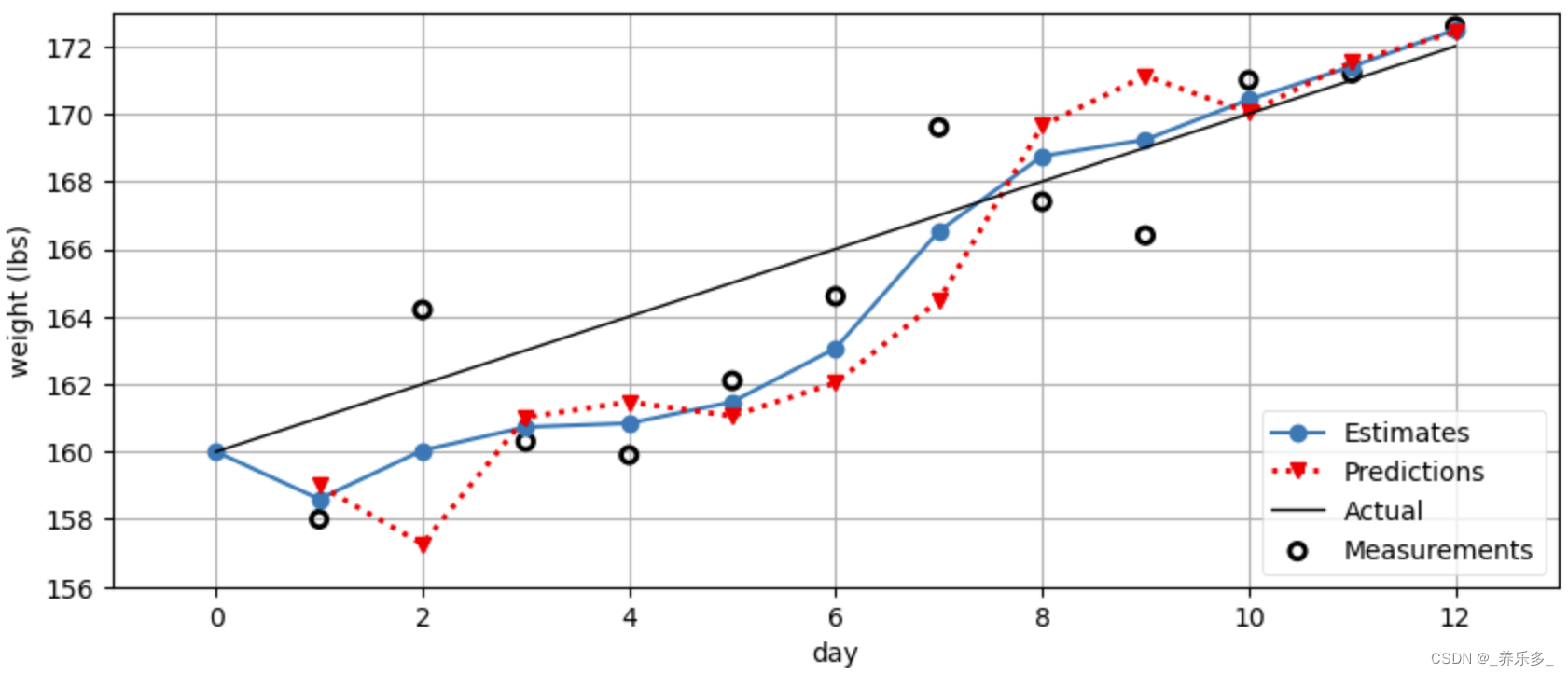
通过一个简单的例子来说明卡尔曼滤波器和贝叶斯滤波器在遥感时间序列数据中的应用。
假设我们有一个遥感传感器,每天对一个湖泊的水位进行观测。由于天气和传感器本身的误差,每次观测都可能存在一定程度的噪声。我们希望通过这些观测数据来估计湖泊的实际水位。
- 卡尔曼滤波器应用:
- 首先,我们使用卡尔曼滤波器来估计湖泊的水位。我们假设湖泊的水位是一个随时间变化的状态,并且假设状态的变化是一个线性模型。卡尔曼滤波器可以不断地根据当前观测值和先前的状态估计值来更新当前状态的估计。
假设在第t天,我们得到了一个观测值z_t,表示湖泊的水位观测值。我们的状态变量为x_t,表示湖泊的实际水位。
卡尔曼滤波器的过程如下:
-
预测步骤(预测状态和协方差):
x_t^- = A * x_t-1 (状态预测)
P_t^- = A * P_t-1 * A^T + Q (协方差预测)
其中,A是状态转移矩阵,P_t^-是预测的协方差矩阵,Q是过程噪声的协方差矩阵。 -
更新步骤(根据观测值更新状态和协方差):
K_t = P_t^- * H^T * (H * P_t^- * H^T + R)^-1 (卡尔曼增益)
x_t = x_t^- + K_t * (z_t - H * x_t^-) (状态更新)
P_t = (I - K_t * H) * P_t^- (协方差更新)
其中,H是观测矩阵,R是观测噪声的协方差矩阵,K_t是卡尔曼增益。 -
通过卡尔曼滤波器,我们可以根据先前的状态估计值和当前观测值,动态地估计湖泊的实际水位,并且减少观测噪声对估计结果的影响。
- 贝叶斯滤波器应用:
接下来,我们考虑使用贝叶斯滤波器来融合多个传感器的观测数据。除了之前的传感器,我们现在引入另外一个传感器,它也每天对湖泊的水位进行观测。
假设第一个传感器的观测值为z_t1,第二个传感器的观测值为z_t2。我们希望根据这两个传感器的观测值来估计湖泊的实际水位x_t。
-
贝叶斯滤波器的过程如下:
根据贝叶斯定理,我们可以得到后验概率分布P(x_t | z_t^1, z_t^2) ∝ P(z_t^1, z_t^2 | x_t) * P(x_t) -
其中,P(z_t^1, z_t^2 | x_t)是给定实际水位x_t时两个传感器观测值的联合概率分布,P(x_t)是先验概率分布,表示我们对实际水位的先前估计。
-
我们可以使用多种方法来估计后验概率分布,例如粒子滤波、扩展卡尔曼滤波等。通过融合多个传感器的数据,我们可以得到对湖泊实际水位的更准确估计。
- 总结:
通过卡尔曼滤波器和贝叶斯滤波器,我们可以对遥感时间序列数据进行状态估计、去除噪声、填补缺失值以及融合多个传感器的数据,从而提高数据质量和提供更精确的估计结果。在实际应用中,滤波器的具体选择和参数设置将取决于具体的数据和应用场景。