1. 思路讲解

1.1 创建dp表

此题采用动态规划的方法，创建一个二维dp表，dp[i][j]表示s[i, j]中最大回文子序列的长度。且我们人为规定 i 是一定小于等于 j 的。

1.2 状态转移方程

在求dp[i][j]时，首先要判断s[i]和s[j]是否相同。

如果 s[i] == s[j]

1. 如果 i == j，说明 i 与 j 的位置相同，此时dp[i][j] 就为 1
2. 如果 i + 1 == j，说明 i 与 j 相邻，此时dp[i][j] 就为2
3. 其他情况下，说明 i 和 j 中间有其他元素，那么此时dp[i][j] = dp[i+1][j-1] + 2；

如果s[i] != s[j]

那么此时，说明不能同时以 i 为开头和以 j 为结尾，我们去掉这种情况寻找一个最大子序列即可。方法就是在 dp[i+1, j] 和 dp[i, j-1] 中选一个最大的即可。即dp[i][j] = max(dp[i+1[j], dp[i][j-1]);

1.3 不需考虑边界问题

在求dp[i][j]的时候，我们可能会用到 i + 1 和 j - 1，在它们有可能越界的时候，一定是 i 等于 j 的时候。我们创建的dp表是二维的，我们可以想到，在可能越界的时候，就是左上角的位置或者右下角的位置，但其实这两个位置满足 i == j，那么dp[i][j] 就会被直接赋值为1，此时就不会用到 i + 1 和 j - 1 了，所以其实我们不用考虑越界的情况。

2. 整体代码

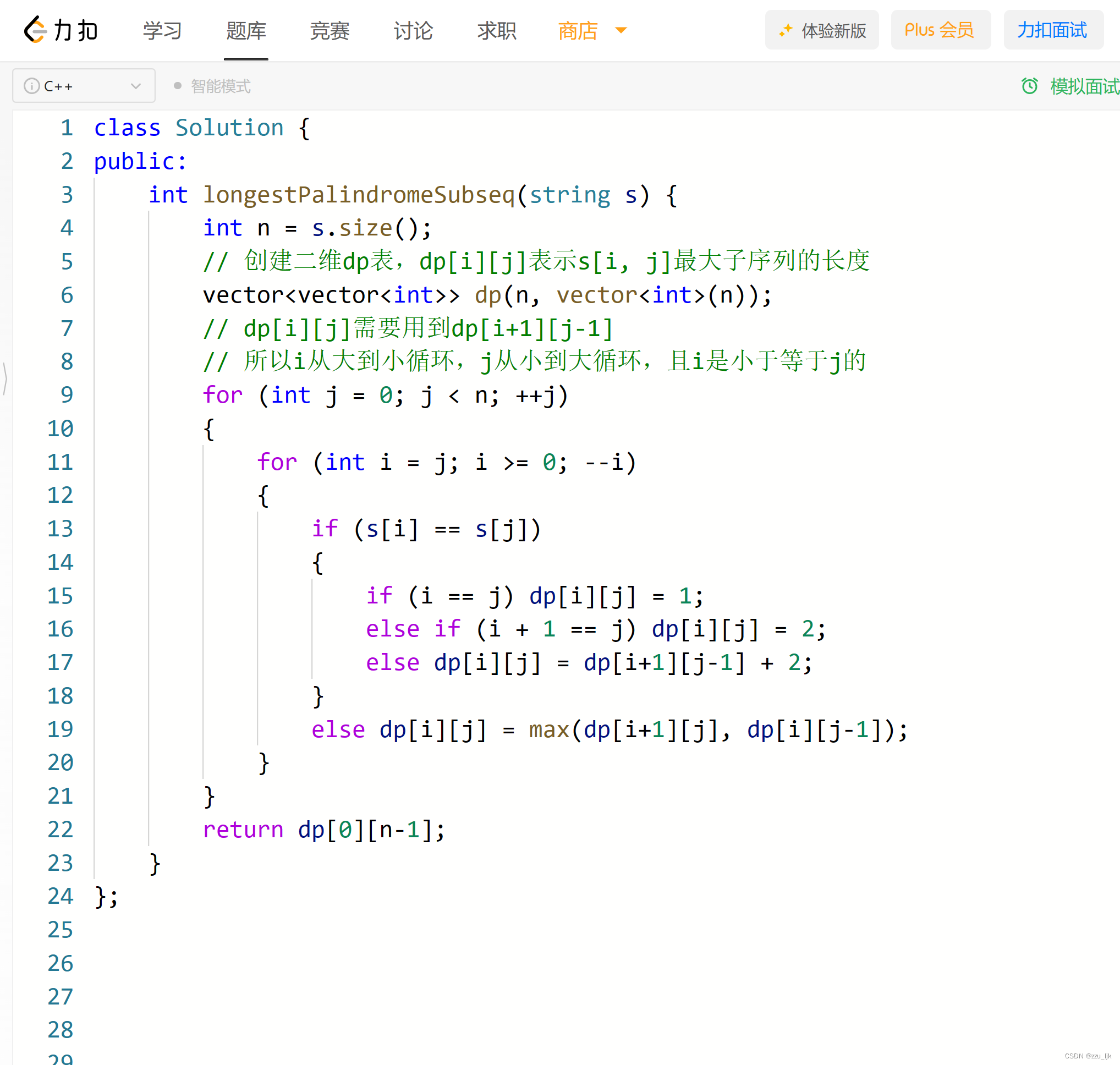
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        // 创建二维dp表，dp[i][j]表示s[i, j]最大子序列的长度
        vector<vector<int>> dp(n, vector<int>(n));
        // dp[i][j]需要用到dp[i+1][j-1]
        // 所以i从大到小循环，j从小到大循环，且i是小于等于j的
        for (int j = 0; j < n; ++j)
        {
            for (int i = j; i >= 0; --i)
            {
                if (s[i] == s[j])
                {
                    if (i == j) dp[i][j] = 1;
                    else if (i + 1 == j) dp[i][j] = 2;
                    else dp[i][j] = dp[i+1][j-1] + 2;
                }
                else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
            }
        }
        return dp[0][n-1];
    }
};