文章目录
- 多源汇最短路:1125. 牛的旅行
- 传递闭包:343. 排序
- 最小环:344. 观光之旅
- 345. 牛站
flody的四个应用:
- 多源汇最短路
- 传递闭包
- 找最小环
- 恰好经过k条边的最短路 倍增
多源汇最短路:1125. 牛的旅行
1125. 牛的旅行 - AcWing题库

直径概念:同一连通块中,两个距离最远的点之间的距离
如何求直径?由于图中存在着两个连通块,所以直接对全图做一个flody,就能更新出任意两点间的距离,距离大于正无穷的一半时,说明两点处于不同连通块中
题目要连接两个连通块,并计算所有连接方法下,原连通块与新连通块中,最大直径的最小值
可以枚举所有的连接方式,维护出新连通块的直径最小值,将其与原连通块的两个直径比较,取三者的最小值即可
假设连接了属于不同连通块的i和j,那么经过这条边的直径等于get_dis(i, j) + dmax(i) + dmax(j),其中get_dis表示两点间的距离,dmax(i)表示在原连通块中,i与距离i最远的点的距离
那么新连通块的直径是原连通块的直径与经过连接两连通块的边的直径中的最大值
最终要在原连通块的直径与新连通块的直径最大值中取min
在计算新连通块的直径最大值时,需要在原连通块与当前新连通块的直径中取max,由于每中不同连接方式都要与原连通块的直径取max,我们可以放到最后在与之取max
先计算经过连接两连通块的边的直径的最大值,在与原连通块的直接取max
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#define x first
#define y second
using namespace std;
typedef pair<double, double> PDD;
const int N = 155;
const double INF = 1e20;
int n;
PDD q[N];
double d[N][N];
double maxd[N];
char g[N][N];
double get_dist(PDD a, PDD b)
{
double dx = a.x - b.x;
double dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ ) cin >> q[i].x >> q[i].y;
for (int i = 0; i < n; i ++ ) cin >> g[i];
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
if (i == j) d[i][j] = 0;
else if (g[i][j] == '1') d[i][j] = get_dist(q[i], q[j]);
else d[i][j] = INF;
for (int k = 0; k < n; k ++ )
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
double r1 = 0;
for (int i = 0; i < n; i ++ )
{
for (int j = 0; j < n; j ++ )
if (d[i][j] < INF / 2)
maxd[i] = max(maxd[i], d[i][j]);
r1 = max(r1, maxd[i]);
}
double r2 = INF;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
if (d[i][j] > INF / 2)
r2 = min(r2, maxd[i] + maxd[j] + get_dist(q[i], q[j]));
cout << r1 << ' ' << r2 << endl;
printf("%.6lf\n", max(r1, r2));
return 0;
}
传递闭包:343. 排序
343. 排序 - AcWing题库

将简洁相连的点连接起来,成为传递闭包
用flody可以在
O
(
n
3
)
O(n^3)
O(n3)的时间复杂度内计算出传递闭包
用邻接矩阵g存储图,传递闭包保存在矩阵d上
g[i][j]为1,表示存在一条从i到j的边,g[i][j]为0表示不存在
初始化:d[i][j] = g[i][j]
flody的更新换为:
d[i][j] |= d[i][k] && d[k][j]
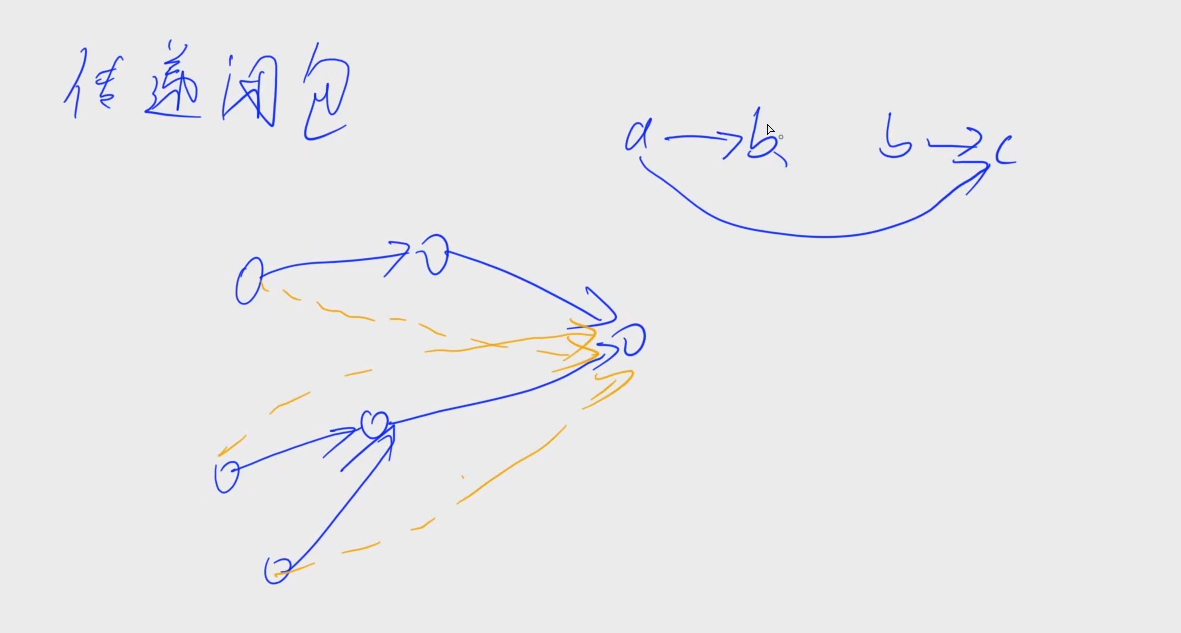
题目中的小于关系就是一条边,每次读取一个小于关系,就在图中添加一条边,然后求传递闭包
三种情况:
- 矛盾:此时
d[i][[i] = 1,表示i存在自环。因为d[i][j] == 1 && d[j][i] == 1,求完传递闭包后d[i][i] = 1 - 情况未确定,
d[i][j]和d[j][i]都为0,表示i和j之间没有边,即没有小于关系 - 情况确定,遍历完d数组,无以上情况,此时情况确定
当情况确定时,如何按小于关系输出变量?
O
(
n
2
)
O(n^2)
O(n2)地暴力搜索所有点,将已经输出的变量进行标记,若当前点是某一条边的终点并且起点未被标记,说明存在小于当前变量的变量,且未被输出
若当前变量不是任意一条边的终点或者起点已经被标记,那么输出该变量并标记
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 26;
int n, m;
bool g[N][N], d[N][N];
bool st[N];
void floyd()
{
memcpy(d, g, sizeof d);
for (int k = 0; k < n; k ++ )
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
d[i][j] |= d[i][k] && d[k][j];
}
int check()
{
for (int i = 0; i < n; i ++ )
if (d[i][i])
return 2;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
if (!d[i][j] && !d[j][i])
return 0;
return 1;
}
char get_min()
{
for (int i = 0; i < n; i ++ )
if (!st[i])
{
bool flag = true;
for (int j = 0; j < n; j ++ )
if (!st[j] && d[j][i])
{
flag = false;
break;
}
if (flag)
{
st[i] = true;
return 'A' + i;
}
}
}
int main()
{
while (cin >> n >> m, n || m)
{
memset(g, 0, sizeof g);
int type = 0, t;
for (int i = 1; i <= m; i ++ )
{
char str[5];
cin >> str;
int a = str[0] - 'A', b = str[2] - 'A';
if (!type)
{
g[a][b] = 1;
floyd();
type = check();
if (type) t = i;
}
}
if (!type) puts("Sorted sequence cannot be determined.");
else if (type == 2) printf("Inconsistency found after %d relations.\n", t);
else
{
memset(st, 0, sizeof st);
printf("Sorted sequence determined after %d relations: ", t);
for (int i = 0; i < n; i ++ ) printf("%c", get_min());
printf(".\n");
}
}
return 0;
}
最小环:344. 观光之旅
344. 观光之旅 - AcWing题库
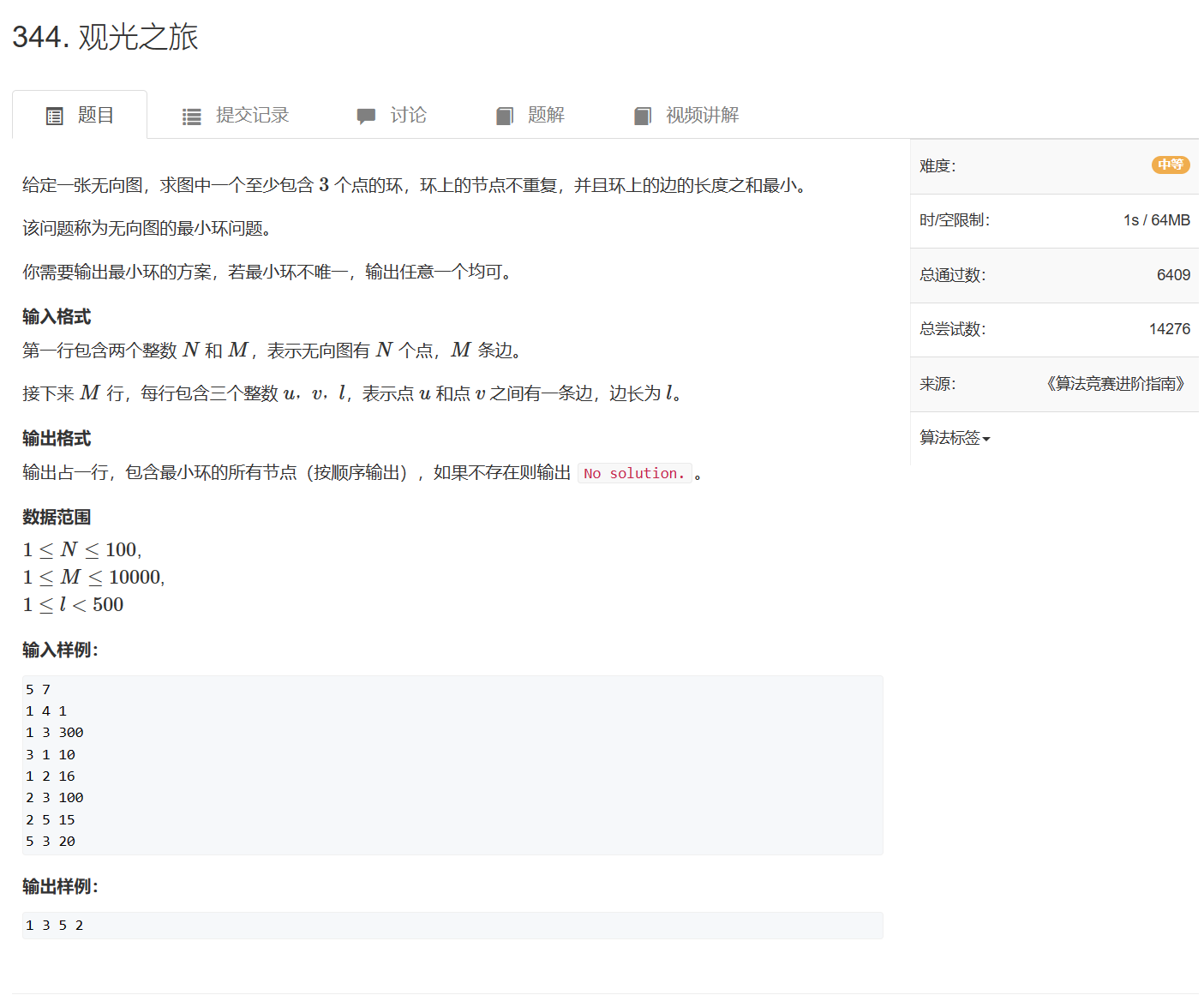
如何求第k类的最小环?
思考flody的三重循环,在第一重k循环时,我们已经知道从i到j只经过1~k-1这些点的最短路径
若i,j,k三者能构成环,那么i和k直接相连,i和j也直接相连
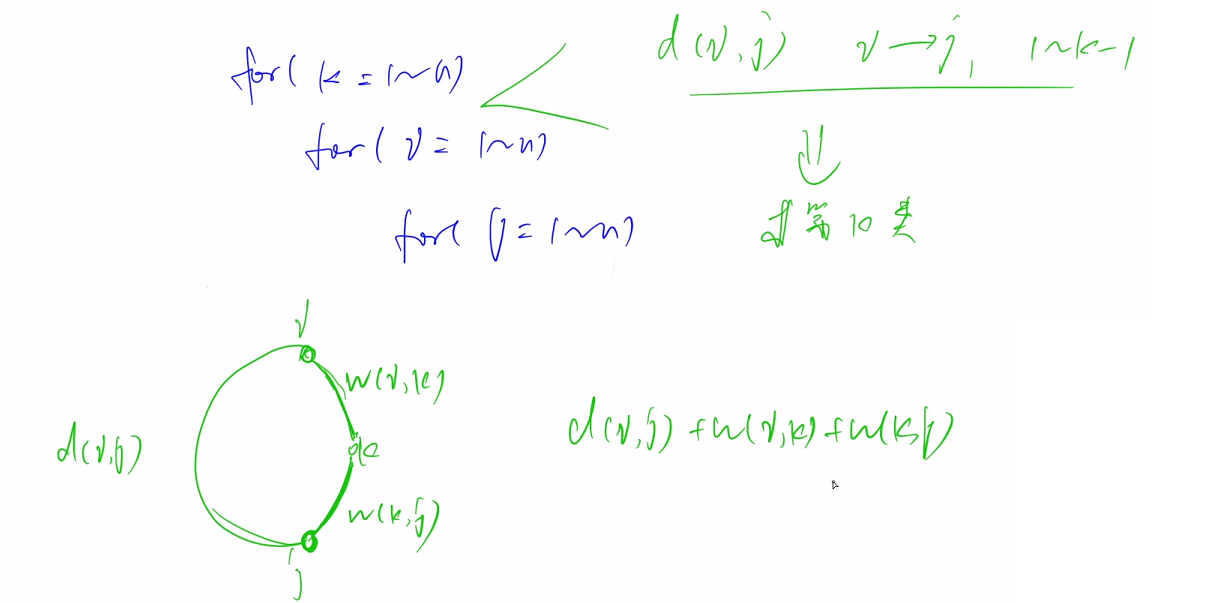
此时i,j,k构成的最小环的长度就等于d[i][j] + g[i][k] + g[k][j]
d[i][j]为i到j的最短距离
所以在循环k时,就可以枚举所有的i和j,得到包含i,j,k三点的最小环,在这些最小环中取min即可
此外,还需要求具体方案
只需要在更新的时候:d[i][j] > d[i][k] + d[k][j]时,记录i到j的最短路经过了k即可,即pos[i][j] = k
求i到j的最短路时,采用递归的方式,get_path(i, j),该函数将顺序输出i到j的最短路中,除了i和j的所有中间点
get_path(i, j),通过pos[i][j]的值,将i到j划分称i到k到j,递归get_path(i, k)与get_path(k, j),直到pos[i][j]为0,说明i到j之间无之间点,即两点之间相连
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 110, M = 20010, INF = 0x3f3f3f3f;
int g[N][N], d[N][N];
int path[N], cnt;
int pos[N][N];
int n, m;
void get_path(int i, int j)
{
if (pos[i][j] == 0) return;
int k = pos[i][j];
get_path(i, k);
path[cnt ++ ] = k;
get_path(k, j);
}
int main()
{
scanf("%d%d", &n, &m);
memset(g, 0x3f, sizeof(g));
for (int i = 1; i <= n; ++ i ) g[i][i] = 0;
for (int i = 1; i <= m; ++ i )
{
int x, y, d;
scanf("%d%d%d", &x, &y, &d);
g[x][y] = g[y][x] = min(g[x][y], d);
}
memcpy(d, g, sizeof(g));
int res = INF;
for (int k = 1; k <= n; ++ k )
{
for (int i = 1; i < k; ++ i )
for (int j = i + 1; j < k; ++ j )
{
if (res > (LL)d[i][j] + g[i][k] + g[k][j])
{
res = d[i][j] + g[i][k] + g[k][j];
cnt = 0;
path[cnt ++ ] = k; // 从k开始记录环
path[cnt ++ ] = i;
get_path(i, j);
path[cnt ++ ] = j;
}
}
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= n; ++ j)
if (d[i][j] > d[i][k] + d[k][j])
{
d[i][j] = d[i][k] + d[k][j];
pos[i][j] = k;
}
}
if (res == INF) puts("No solution.");
else for (int i = 0; i < cnt; ++ i ) printf("%d ", path[i]);
return 0;
}
一些需要注意的地方:res > (LL)d[i][j] + g[i][k] + g[k][j]
不开LL的话,可能三个INF相加会导致爆int
枚举最小环时,j从i+1开始,保证j比i的同时,也保证最小环中至少有三个点
没看懂,先跳过
345. 牛站
345. 牛站 - AcWing题库
flody的变形,表示的状态发生变化,
f
(
k
,
i
,
j
)
f(k, i, j)
f(k,i,j)表示从i到j,恰好经过k条边的最短路
d
[
a
+
b
,
i
,
j
]
=
d
[
a
,
i
,
k
]
+
d
[
b
,
k
,
j
]
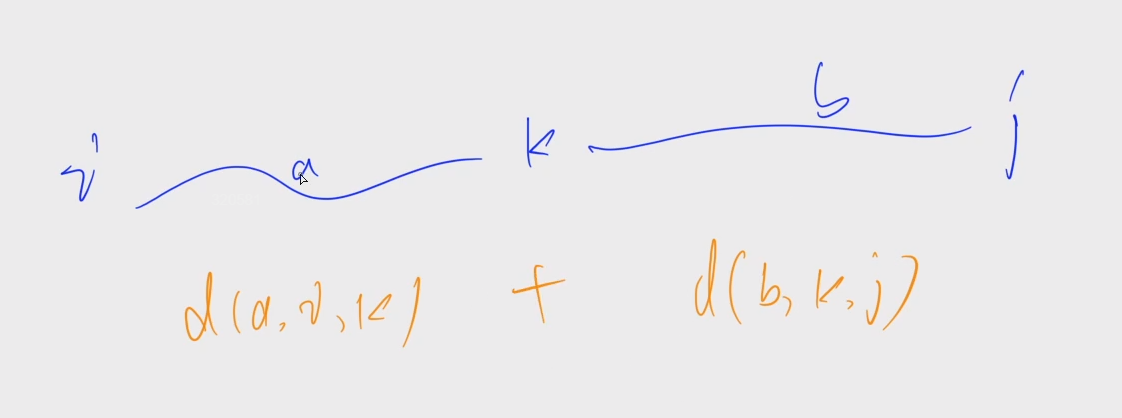
d[a+b, i, j] = d[a, i, k] + d[b, k, j]
d[a+b,i,j]=d[a,i,k]+d[b,k,j]
从i到j恰好经过a+b条边的最短路径,假设中间点为k,将路径划分称两段,经过a条边从i到k,经过b条边从k到j。两段分别取最短路径,相加得到我们需要的最短路径
枚举所有的k,取min后就能得到
d
[
a
+
b
,
i
,
j
]
d[a+b, i, j]
d[a+b,i,j]
枚举所有的k后,枚举不同的i和j,转换成代码就是flody的形式