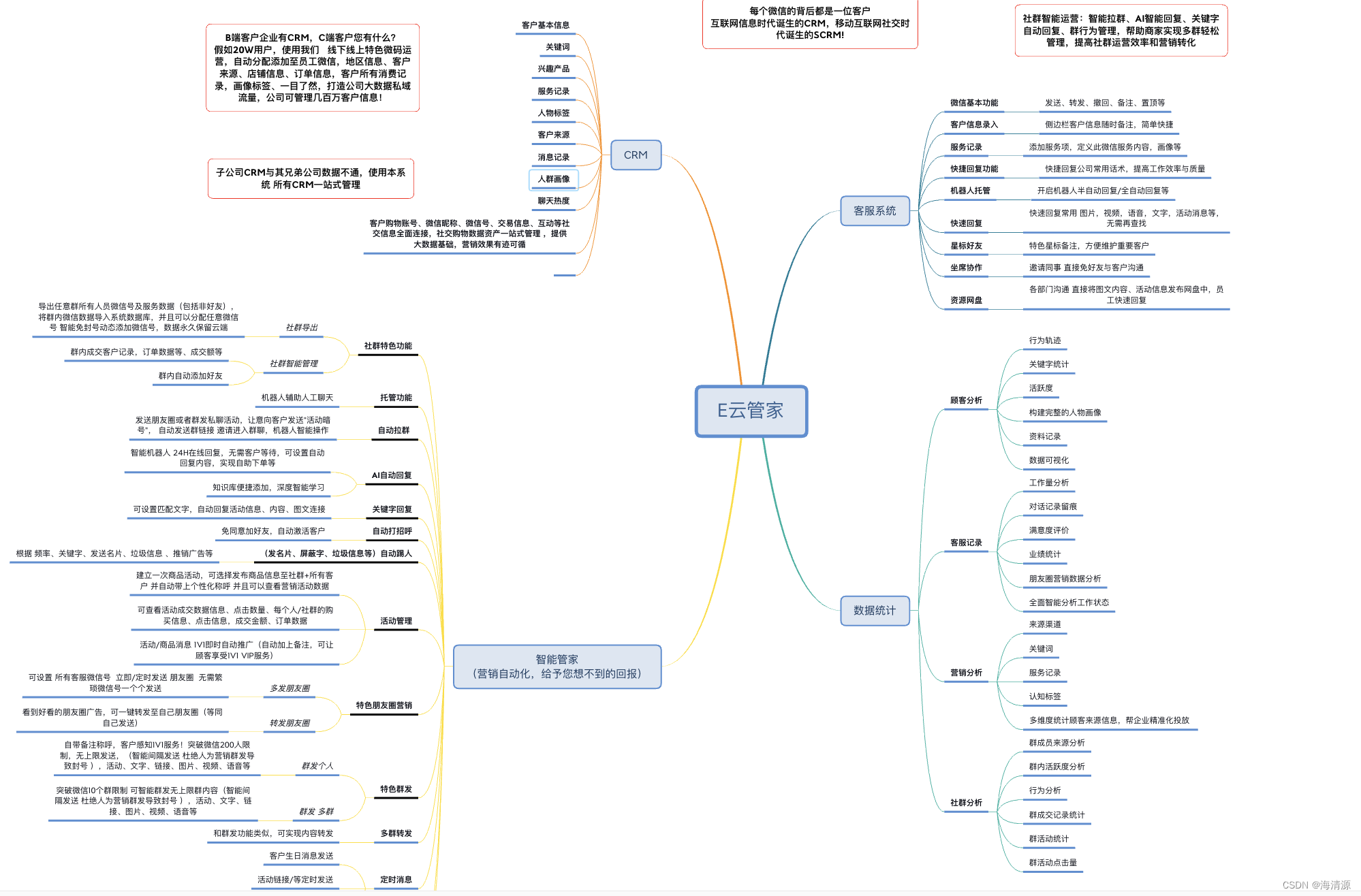
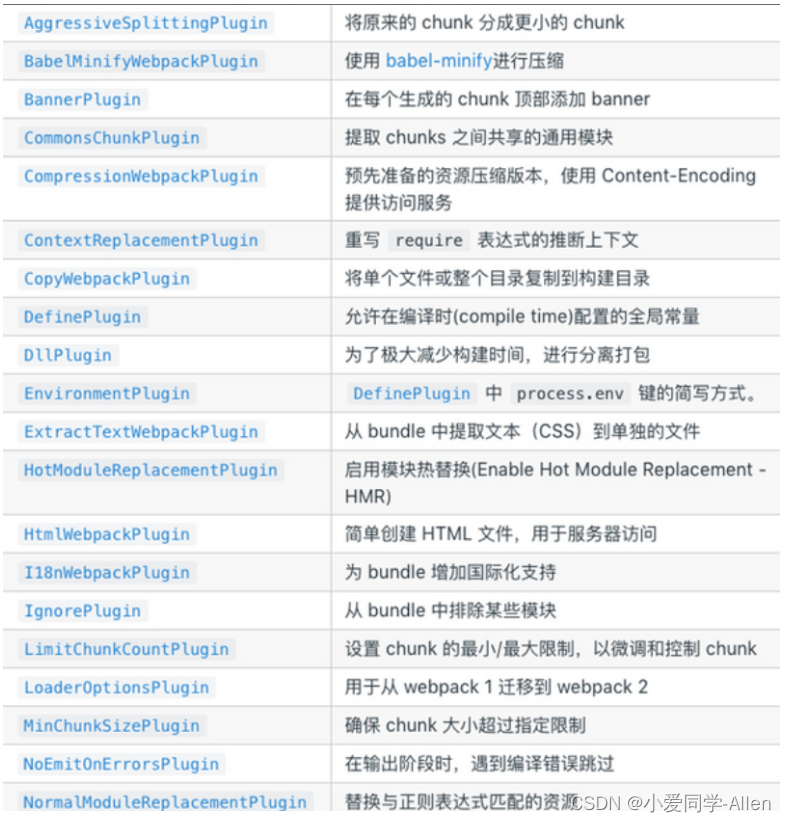
效果图 

 实现代码

<el-table-column prop="attachment"  label="合同附件" width="250" show-overflow-tooltip>
            <template slot-scope="scope">
              <div v-if="scope.row.cceedcAppendixInfoList &&
                scope.row.cceedcAppendixInfoList.length > 0
                ">
                <el-button type="text" size="small" v-for="(val, key, i) in scope.row.cceedcAppendixInfoList" :key="i"
                  @click.native.prevent="downContractFile(val)">{{ val.appendixOriginalName }}</el-button>
              </div>
              <div v-else>
                <span>暂无</span>
              </div>
            </template>
          </el-table-column>

    downContractFile(val) {
      request({
        url: "/appendix/downloadFile",
        method: "get",
        params: {
          appendixStorageName: val.appendixStorageName,
          appendixOriginalName: val.appendixOriginalName,
        },
        responseType: "blob",
      }).then((res) => {
        var filename = val.appendixOriginalName;
        var downloadElement = document.createElement("a");
        var href = window.URL.createObjectURL(new Blob([res])); //创建下载的链接
        downloadElement.href = href;
        downloadElement.setAttribute("download", filename);
        document.body.appendChild(downloadElement);
        downloadElement.click(); //点击下载
        document.body.removeChild(downloadElement); //下载完成移除元素
        window.URL.revokeObjectURL(href); //释放掉blob对象
      });
    },