完整思路下载链接：这里获取

2023华数杯全国大学生数学建模竞赛题目

B 题不透明制品最优配色方案设计

日常生活中五彩缤纷的不透明有色制品是由着色剂染色而成。因此，不透明制品的配色对其外观美观度和市场竞争力起着重要作用。然而，传统的人工配色存在一定的局限性，如主观性强、效率低下等。因此，研究如何通过计算机方法来实现不透明制品的配色具有重要意义。

光通过物体传播有吸收、反射和透射三种方式。对于不透明制品来说，大部分光线会被其表面吸收或反射。吸收和反射的光线在经过透明度等校正后按波长分解成不同的颜色成分，形成光谱图。该光谱图通常由400-700nm 波段的各色光组成。为简化计算，最终配色后的颜色的反射率20nm 为间隔的光谱数据来表示。对于不透明材料而言，吸收系数K/散射系数S 的比值与反射率R 之间存在一定关系，具体请参考文献【1】《计算机配色理论及算法的研究》中的K-M光学模型。

基于光学模型得到的颜色参数，可应用于色差的计算。通常，使用色差（不超过1）来作为配色效果好坏的标准。色差计算方法参考文献【2】《基于CIELAB均匀颜色空间和聚类算法的混纺测色研究》中的CIELAB 色彩空间的总色差计算法。其中颜色参数L*(明度)、a*(红绿色度)和b*（黄蓝色度）计算中出现的三刺激值XYZ 的计算方法如下：

$$X=k{\int }_{400}^{700}S(\lambda )\bar{x}(\lambda )R(\lambda )d(\lambda )$$
$$Y=k{\int }_{400}^{700}S(\lambda )\bar{y}(\lambda )R(\lambda )d(\lambda )$$
$$Z=k{\int }_{400}^{700}S(\lambda )\bar{z}(\lambda )R(\lambda )d(\lambda )$$

其中，$S(\lambda )$为光谱能量分布，$\bar{x}(\lambda )\bar{x}(\lambda )\bar{x}(\lambda )$为观察者光谱三刺激值，$S(\lambda )分别与\bar{x}(\lambda )\bar{x}(\lambda )\bar{x}(\lambda )$相乘为固定值见附件1。$R(\lambda )$为光谱反射率，k值约为0.1，$d(\lambda )$为测量物体反射率波长间隔，本题$d(\lambda )=20nm$。

不透明制品配色问题，就是基于光学模型，设计不透明制品的配色模型。相较于人工配色，节省大量人力、物力和财力，对减少能耗具有重要意义。

针对某一不透明制品，已知红、黄、蓝3 种着色剂在不同浓度不同波长的K/S 值以及基底材料在不同波长下的K/S 值，见附件2。其中，浓度=着色剂克重/基材重量。每个着色剂的吸收系数K/散射系数S 的比值具有加和性，详见文献【1】《计算机配色理论及算法的研究》中的K-M 单常数理论。现有10 个目标样(二到三种着色剂混合制成)的R 值，见附件3。结果展示请保留4 位小数。

请建立数学模型解决如下几个问题：

✅ 问题1

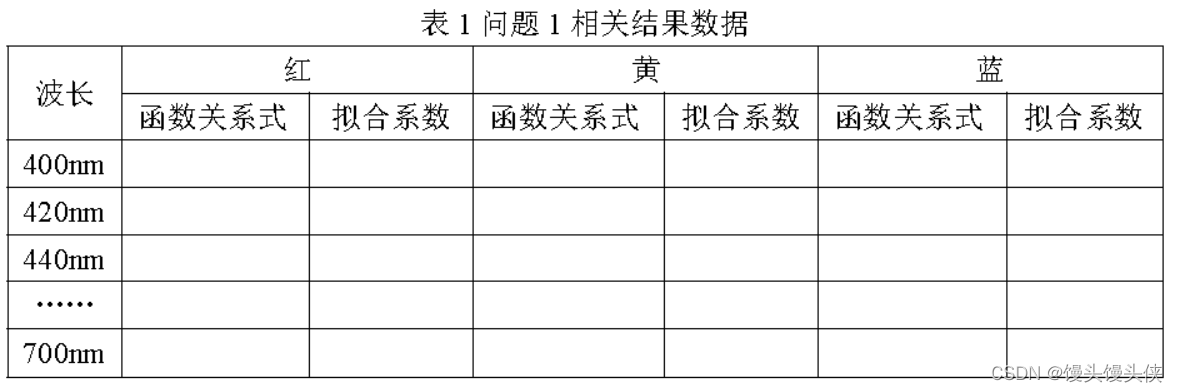
请分别计算附件2 中三种着色剂在不同波长下K/S 与浓度的关系，并将关系式与拟合系数填写在表格中。

B题需要用到不少运筹规划类相关算法，需要用到比如单目标规划、多目标规划、动态规划等。这里对第一问进行简单的分析，后续会提供更具体的分析与建模。

思路清晰：把需要用到的和问题理清关系，KS值和R的关系，KS和浓度的关系，浓度和基地材料的关系，KS值和色差计算的关系，这些附件和文件都能得到。

问题1建模思路

问题一需要计算附件2中三种着色剂在不同波长下的KS值与浓度的关系。首先，我们需要选择适当的拟合函数，常见的选择有多项式、指数、对数拟合等。

当然更好的做法是先查找文献，看看是否有KS值和浓度相关的推导公式，再进一步拟合相关的系数，这样得到的结果更好。参考文献【1】、【2】里面有相关计算公式可直接利用

在这里，我们使用简单的多项式拟合来计算得到KS值和浓度的关系，比较不同次项拟合的结果，选取更好的方案。推荐使用matlab、python做拟合。

具体步骤如下：

1 根据附件2中的数据，将波长和KS值与浓度分别记为 x 和 y

2 选择一个合适的多项式拟合函数形式，或者查找文献找到相关推导公式做基本形式。

3 将拟合函数带入到拟合问题中，得到一个最小化误差的目标函数

4 使用最小二乘法或其他拟合方法求解该目标函数，得到拟合系数。

综上所述，我们可以得到红黄蓝三种着色剂在不同波长下的KS值与浓度的关系式，并将关系式和其拟合系数填写在表格1中。

✅ 问题2

请建立不透明制品配色的优化模型。在已知目标样的R 值（附件3）的前提下，基于光谱三刺激值加权表（附件1）与着色剂K/S 基础数据库（附件2），运用优化模型配出与目标样的色差最为接近的10 个不同配方，要求色差小于1。

问题2建模思路

这是一个最优化问题，我们需要知道如何判断色查是否接近，根据得到相关的计算公式，首先需要明白配方是指什么？

第一步：将表1中的光谱三刺激值加权表与表2中的基础数据库表合并，计算出不同着色剂的色差值，并将结果保存。

第二步：计算得到附件3不同样本的色差。

第三步建立优化模型：将配方和样本的色差差值作为目标函数，得到不同着色剂浓度的组合，建立一个最小化色差的优化模型。

第四步确定约束条件：设置色差小于1的约束条件，确保选出的配方与目标样的色差小于1。

第五步求解优化问题：使用数学优化算法，如fmincon、梯度下降法、粒子群算法、遗传算法等，求解建立的优化问题，得到与目标样的色差最为接近的10个不同配方。

✅ 问题3

在问题2 的基础上，考虑成本控制和批量配色，改进配色模型。对2kg 的基底材料进行配色，求出与目标样（附件3）之间色差最为接近的10 个不同配方，要求色差小于1。色母粒单位克重价格见附件4。

问题3建模思路

该问基于问题二的拓展，约束条件得加入成本的控制，基地材料不能超过2kg，从而限制了着色剂的选择。

✅ 问题4

在实际生产中，配色所需要的着色剂越少越好，基于此，在问题3的基础上，寻找附件3 中前5 个样本的最优的配色方案，要求每个样本配出5个不同的配方且色差小于1。

问题4建模思路

将优化模型升级成多目标规划即可。

提供的数据和资料：

1.附件1（光谱三刺激值加权表）
2.附件2（不同浓度不同波长的K/S 值）
3.附件3（10 个样品的R 值）
4.附件4（染料价格）
5.参考文献【1】姜鹏飞. 计算机配色理论及算法的研究[D/OL]. 中原工学院,2016
6.参考文献【2】王林吉. 基于CIELAB 均匀颜色空间和聚类算法的混纺测色研究[D]. 浙江理工大学, 2011.