1案例背景

1.1连续Hopfield神经网络概述

1.网络结构
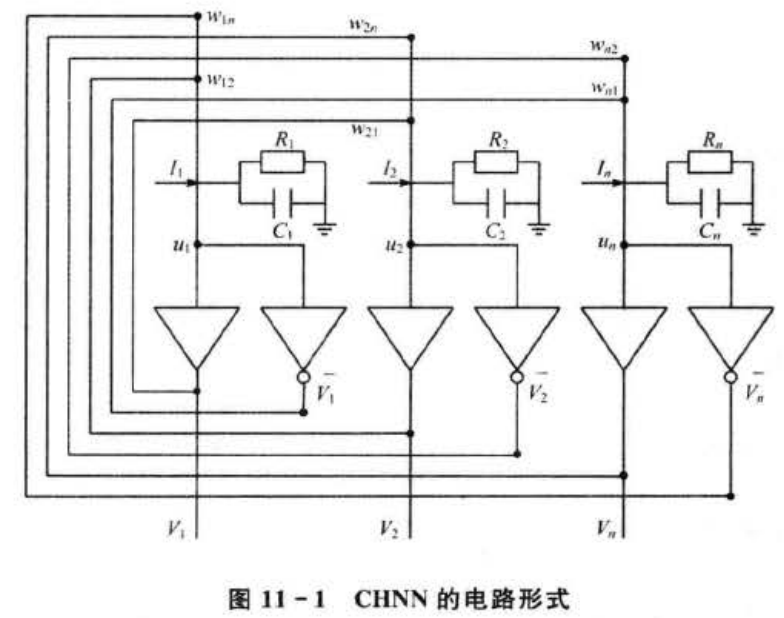
连续Hopfield神经网络(Continuous Hopfield Neural Network,CHNN)的拓扑结构和离散Hopfield神经网络的结构类似,如图11-1所示。连续Hopfield网络和离散Hopfield 网络的不同点在于其传递函数不是阶跃函数,而是连续函数。

与离散型Hopfield神经网络不同,由于连续型Hopfield神经网络在时间上的连续性,其工作方式为并行(同步)方式。
J.J. Hopfield利用模拟电路(电阻、电容和运算放大器)实现了对网络的神经元的描述,如图11-1所示。假设神经元jj=1,2,…,n)的内部膜电位状态用U,表示,细胞膜输入电容为C,,细胞膜的传递电阻为R,,输出电压为V,,外部输入电流用I,表示。其中,R,和C,的并联模拟了生物神经元的时间常数，w;模拟了神经元间的突触特性,运算放大器模拟了神经元的非线性特性，Ij相当于阙值。由基尔霍夫电流定律(Kirchhoff's Current Law,KCL)可以得出:

2.网络稳定性
关于连续型Hopfield神经网络的稳定性,J.J.Hopfield利用定义的能量函数进行了详细的推导和证明,具体证明过程如下。能量函数E(t)定义为:

从上述证明过程可以看出：

①当网络神经元的传递函数单调递增且网络权系数矩阵对称时，网络的能量会随着时间变化下降或保持不变；

②当且仅当神经元的输出不再随时间变化而变化时，网络的能量才会不变。

3.优化计算

在实际应用中，如果将一个最优化问题的目标函数转换成连续Hopfield神经网络的能量函数，把问题的变量对应于网络中神经元的状态，那么Hopfield神经网络就能够用于解决优化组合问题。即当网络的神经元状态趋于平衡点时，网络的能量函数也趋于最小值，网络由初态向稳态收敛的过程就是目标函数优化计算的过程。

1.2组合优化问题概述

组合优化(combinatorial optimization)问题的目标是从组合问题的可行解集中求出最优解组合优化往往涉及排序、分类、筛选等问题,是运筹学的一个重要分支。典型的组合优化问题有旅行商问题(Traveling Salesman Problem,TSP)、加工调度问题(scheduling problem,如 Flow - Shop,job-shop),0-1背包问题(knapsackproblem)、装箱问题(bin packing problem),图着色问题(graph coloring problem)、聚类问题(clustering prob-lem)等。这些问题描述非常简单,并且有很强的工程代表性,但最优化求解很困难,其主要原因是求解这些问题的算法运行时,需要极长的运行时间与极大的存储空间,以致根本不可能在现有的计算机上实现,即会产生所谓的“组合爆炸”问题。正是这些问题的代表性和复杂性激起了人们对组合优化理论与算法的研究兴趣。

利用神经网络解决组合优化问题是神经网络应用的一个重要方面。将Hopfield网络应用于求解组合优化问题,把目标函数转化为网络的能量函数,把问题的变量对应到网络的神经元的状态,这样，当网络的能量函数收敛于极小值时,问题的最优解也随之求出。由于神经网络是并行计算的,其计算量不会随着维数的增加而发生指数性“爆炸”,因而对于优化问题的高速计算特别有效。

1.3问题描述

旅行商(TSP)问题的描述是:在N个城市中各经历一次后再回到出发点,使所经过的路程最短。若不考虑方向性和周期性，在给定N的条件下,可能存在的闭合路径数目为0.5×(N-1)!。当N较大时,枚举法的计算量之大难以想象。现对于一个城市数量为10的TSP问题,要求设计一个可以对其进行组合优化的连续型 Hopfield神经网络模型,利用该模型可以快速地找到最优(或近似最优)的一条路线。

2模型建立

2.1设计思路

由于连续型Hopfield神经网络具有优化计算的特性,因此将TSP问题的目标函数(即最短路径)与网络的能量函数相对应,将经过的城市顺序与网络的神经元状态相对应。这样,由连续型 Hopfield神经网络的稳定性理论可知,当网络的能量函数趋于最小值时,网络的神经元状态也趋于平衡点,此时对应的城市顺序即为待求的最佳路线。

2.2设计步骤

依据设计思路,将TSP问题映射为一个连续型Hopfield神经网络主要分为以下几个步骤,如图11-2所示。

1．模型映射
为了将TSP问题映射为一个神经网络的动态过程,Hopfield采取了换位矩阵的表示方法,用 NXN矩阵表示商人访问N个城市。例如,有5个城市A,B,C,D,E,访问路线是A→C→E→D→B,则 Hopfield网络输出所代表的有效解对应的二维矩阵如表11-1所列。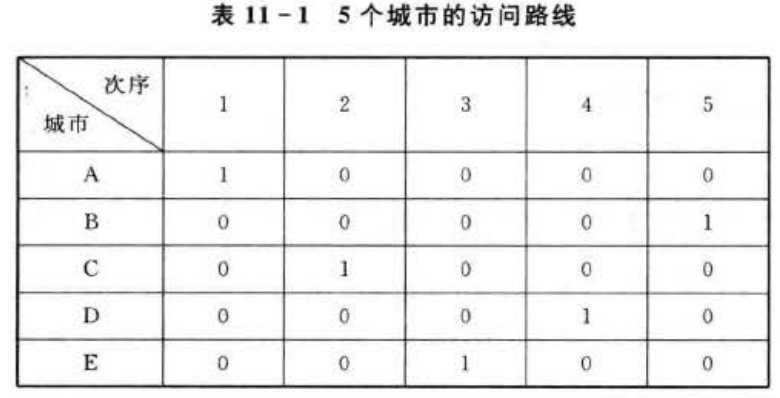

        对于N个城市 TSP问题,需用NXN个神经元来实现,而每行每列都只能有一个1,其余为0,矩阵中1的和为N,该矩阵称为换位矩阵。
        2.构造网络能量函数和动态方程
        如前文所述，设计的 Hopfield神经网络的能量函数是与目标函数(即最短路径)相对应的。同时,应该考虑到有效解(路线)的实际意义,即换位矩阵的每行每列都只能有一个1。因此,网络的能量函数包含目标项(目标函数)和约束项(换位矩阵)两部分。这里,将网络的能量函数定义为:

3. 初始化网络

H op ield 神经网络迭代过程对网络的能量函及动态方程的系数十分敏感，在总结前人经验及多次实验的基础上，网络输入初始化选取如下：

        在式(11-7)、式(11-8)中,取A=200,D=100;采样时间设置为step=0.000 1,迭代次数为10000.
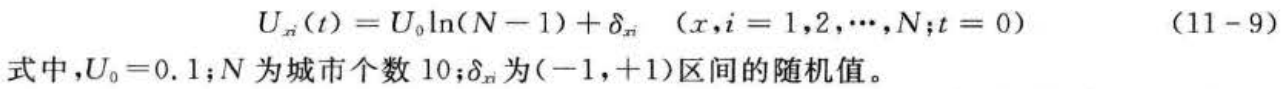
        4．优化计算
        当网络的结构及参数设计完成后,迭代优化计算的过程就变得非常简单,具体步骤如下。

3MATLAB 实现

主函数如下：

%% 连续Hopfield神经网络的优化—旅行商问题优化计算

%% 清空环境变量、定义全局变量
clear all
clc
global A D

%% 导入城市位置
load city_location

%% 计算相互城市间距离
distance = dist(citys,citys');

%% 初始化网络
N = size(citys,1);
A = 200;
D = 100;
U0 = 0.1;
step = 0.0001;
delta = 2 * rand(N,N) - 1;
U = U0 * log(N-1) + delta;
V = (1 + tansig(U/U0))/2;
iter_num = 10000;
E = zeros(1,iter_num);

%% 寻优迭代
for k = 1:iter_num  
    % 动态方程计算
    dU = diff_u(V,distance);
    % 输入神经元状态更新
    U = U + dU*step;
    % 输出神经元状态更新
    V = (1 + tansig(U/U0))/2;
    % 能量函数计算
    e = energy(V,distance);
    E(k) = e;  
end

 %% 判断路径有效性
[rows,cols] = size(V);
V1 = zeros(rows,cols);
[V_max,V_ind] = max(V);
for j = 1:cols
    V1(V_ind(j),j) = 1;
end
C = sum(V1,1);
R = sum(V1,2);
flag = isequal(C,ones(1,N)) & isequal(R',ones(1,N));

%% 结果显示
if flag == 1
   % 计算初始路径长度
   sort_rand = randperm(N);
   citys_rand = citys(sort_rand,:);
   Length_init = dist(citys_rand(1,:),citys_rand(end,:)');
   for i = 2:size(citys_rand,1)
       Length_init = Length_init+dist(citys_rand(i-1,:),citys_rand(i,:)');
   end
   % 绘制初始路径
   figure(1)
   plot([citys_rand(:,1);citys_rand(1,1)],[citys_rand(:,2);citys_rand(1,2)],'o-')
   for i = 1:length(citys)
       text(citys(i,1),citys(i,2),['   ' num2str(i)])
   end
   text(citys_rand(1,1),citys_rand(1,2),['       起点' ])
   text(citys_rand(end,1),citys_rand(end,2),['       终点' ])
   title(['优化前路径(长度：' num2str(Length_init) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 计算最优路径长度
   [V1_max,V1_ind] = max(V1);
   citys_end = citys(V1_ind,:);
   Length_end = dist(citys_end(1,:),citys_end(end,:)');
   for i = 2:size(citys_end,1)
       Length_end = Length_end+dist(citys_end(i-1,:),citys_end(i,:)');
   end
   disp('最优路径矩阵');V1
   % 绘制最优路径
   figure(2)
   plot([citys_end(:,1);citys_end(1,1)],...
       [citys_end(:,2);citys_end(1,2)],'o-')
   for i = 1:length(citys)
       text(citys(i,1),citys(i,2),['  ' num2str(i)])
   end
   text(citys_end(1,1),citys_end(1,2),['       起点' ])
   text(citys_end(end,1),citys_end(end,2),['       终点' ])
   title(['优化后路径(长度：' num2str(Length_end) ')'])
   axis([0 1 0 1])
   grid on
   xlabel('城市位置横坐标')
   ylabel('城市位置纵坐标')
   % 绘制能量函数变化曲线
   figure(3)
   plot(1:iter_num,E);
   ylim([0 2000])
   title(['能量函数变化曲线(最优能量：' num2str(E(end)) ')']);
   xlabel('迭代次数');
   ylabel('能量函数');
else
   disp('寻优路径无效');
end

图11-3所示为随机产生的初始路径,所经过的路径长度为5.3616。

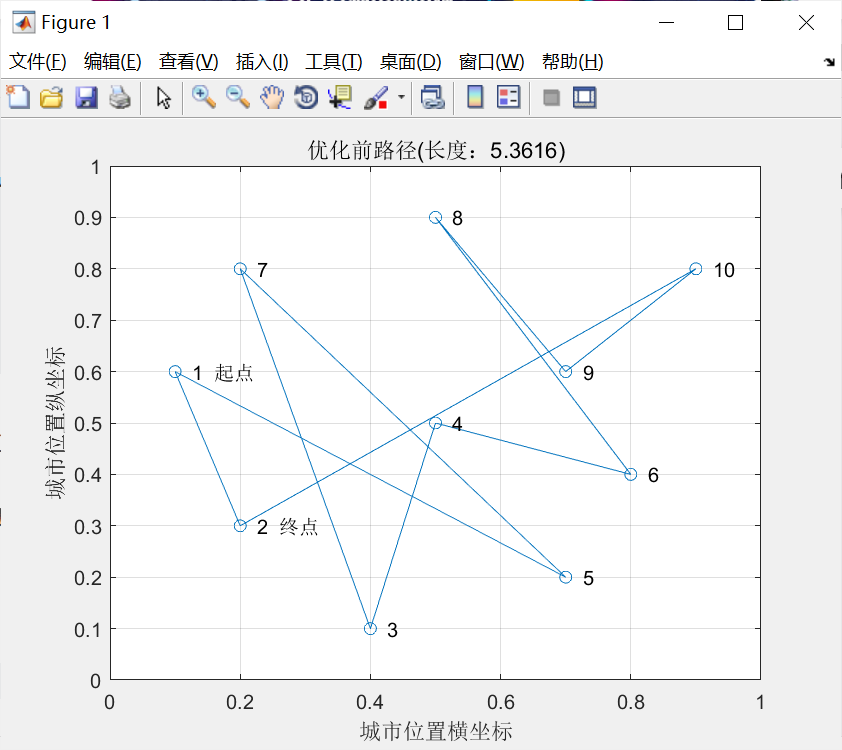
经过连续型Hopfield神经网络优化后,寻找到的优化路径长度为3.0383,如图11-4所示。

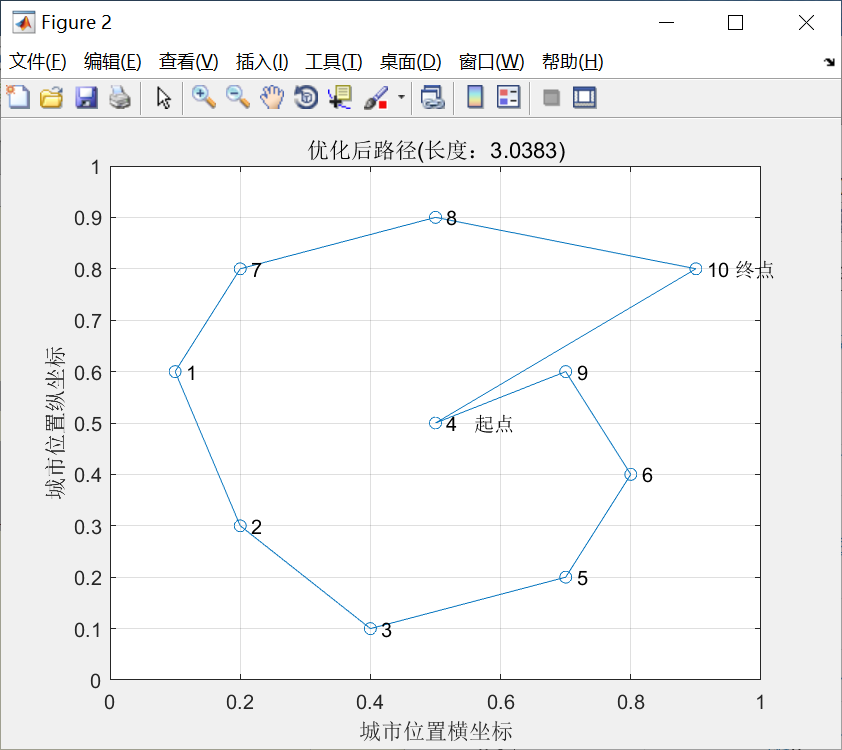
能量函数随迭代过程变化的曲线如图11-5所示,从图中可以看出,网络的能量随着迭代过程不断减少。当网络的能量变化很小时,网络的神经元状态也趋于平衡点,此时对应的城市顺序即为待求的优化路径。
结果表明,利用连续型Hopfield神经网络,可以快速准确地解决 TSP问题。同理,对于其他利用枚举法会产生“组合爆炸”的组合优化问题,利用连续型Hopfield神经网络也可以进行优化计算。

4案例扩展

4.1结果比较

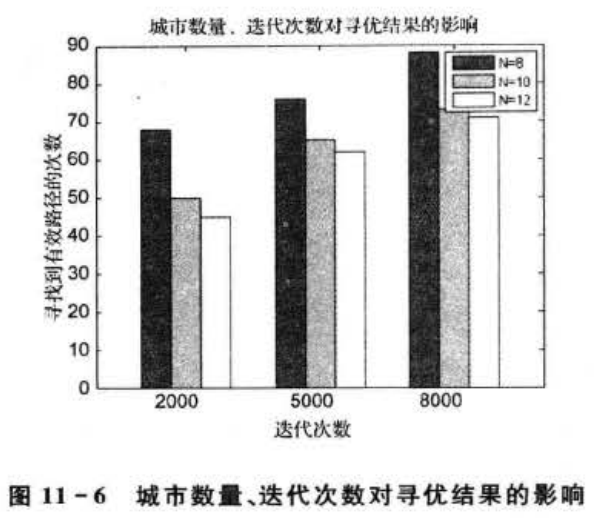
图11-6列出了在进行100次的实验中,寻找到有效路径的次数与城市数量和迭代次数的关系。从表中可以看出,随着城市数量的增加,Hopfield 神经网络寻优的效果越来越差,增加迭代次数,可以改善寻优的效果,但并非迭代次数越多越好,还得结合实际问题进行具体分析,

4.2 案例扩展

利用连续型Hopfield神经网络,将待优化的目标函数及相对应的约束条件转化为能量函数,将问题的变量对应神经网络神经元的状态。当Hopfield神经网络的输出状态趋于平衡点时,能量函数对应的便是待优化问题的最优解。利用此思路,可以快速,准确地解决各种优化问题,如选址优化、轴承设计优化等。另外,能量函数,网络参数会对优化结果产生很大的影响,许多专家学者对这些问题进行了广泛深入的研究。