礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

链接: 剑指 Offer 47. 礼物的最大价值

示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

1.状态表示

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：

1. i. 从 [i, j] 位置出发，……；
2. ii. 从起始位置出发，到达 [i, j] 位置，……；

这⾥选择第⼆种定义状态表⽰的⽅式：
dp[i][j] 表⽰：⾛到 [i, j] 位置处，此时的最⼤价值。

2.状态转移方程

对于 dp[i][j] ，我们发现想要到达 [i, j] 位置，有两种⽅式：

1. i. 从 [i, j] 位置的上⽅ [i - 1, j] 位置，向下⾛⼀步，此时到达 [i, j] 位置能 拿到的礼物价值为 dp[i - 1][j] + grid[i][j] ；
2. ii. 从 [i, j] 位置的左边 [i, j - 1] 位置，向右⾛⼀步，此时到达 [i, j] 位置能 拿到的礼物价值为dp[i][j - 1] + grid[i][j]

我们要的是最⼤值，因此状态转移⽅程为：

dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] 

3. 初始化

为了解决一些边界条件，我们可以添加辅助节点，
在本题中，「添加⼀⾏」，并且「添加⼀列」后，所有的值都为 0 即可。

4. 填表顺序
根据「状态转移⽅程」，填表的顺序是「从上往下填写每⼀⾏」，「每⼀⾏从左往右」

5. 返回值
应该返回 dp[m][n] 的值。

代码：

 int maxValue(vector<vector<int>>& grid) {
        int n=grid.size();
        int m=grid[0].size();
        vector<vector<int>> dp(n+1,vector<int>(m+1));

        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                dp[i][j]=max(dp[i][j-1],dp[i-1][j])+grid[i-1][j-1];
            }
        }
        return dp[n][m];
    }

931. 下降路径最小和

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

链接: 下降路径最小和

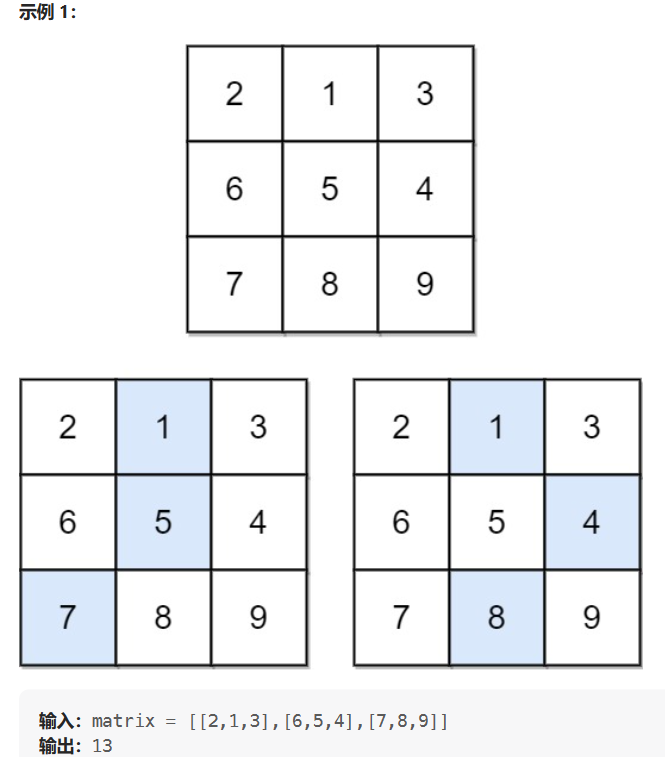
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

1.状态表示

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：

1. i. 从 [i, j] 位置出发，……；
2. ii. 从起始位置出发，到达 [i, j] 位置，……；

这⾥仍选择第⼆种定义状态表⽰的⽅式：
dp[i][j] 表⽰：⾛到 [i, j] 位置处，所有下降路径中的最⼩和。

2.状态转移方程

对于 dp[i][j] ，我们发现想要到达 [i, j] 位置，有三种⽅式：

1. i. 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置；
2. ii. 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置；
3. iii. 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置；

我们要的是三种情况下的「最⼩值」，然后再加上矩阵在 [i, j] 位置的值。
于是

dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +1])) + matrix[i][j] 

3. 初始化

为了解决一些边界条件，我们可以添加辅助节点，
在本题中，需要「加上⼀⾏」，并且「加上两列」。所有的位置都初始化为⽆穷⼤，然后将第⼀⾏初始化为 0 即可。

4. 填表顺序
填表的顺序是 从上往下

5. 返回值
注意这⾥不是返回 dp[m][n] 的值！
题⽬要求「只要到达最后⼀⾏」就⾏了，因此这⾥应该返回「dp表中最后⼀⾏的最⼩值」。

代码：

    int minFallingPathSum(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int> (n+2,INT_MAX));

        for(int i=0;i<n+2;i++) dp[0][i]=0;//初始化第一行的值
        int count=0;
        
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];
            }

        }

        int ret=INT_MAX;//返回值
        for(int i=1;i<=n;i++) ret=min(ret,dp[n][i]);
        return ret;
    }