题目来源：https://leetcode.cn/problems/last-stone-weight-ii/description/

 

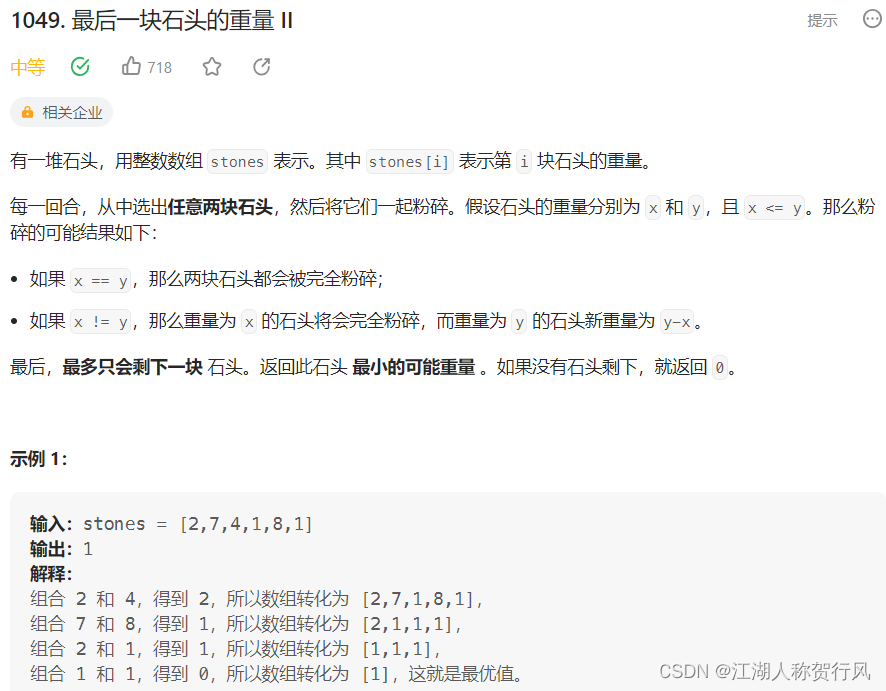
 C++题解（思路来源代码随想录）：本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。

动规五步曲：

1. 确定dp数组以及下标的含义。dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”
2. 确定递推公式。01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);  本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3. dp数组如何初始化。既然 dp[j]中的j表示容量，那么最大容量（重量）就是所有石头的重量和。而我们要求的target其实只是最大重量的一半。
4. 确定遍历顺序。如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！
5. 举例推导dp数组

// 自己的版本
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        int len = stones.size();
        if(len == 1) return stones[0];
        int sum = 0;
        for(int i = 0; i < len; i++){
            sum += stones[i];
        }
        int maxheavy = 0;
        if(sum%2 == 1) maxheavy = (sum-1)/2;
        else maxheavy = sum/2;
        vector<int> dp(maxheavy+1, 0);
        for(int j = 0; j < len; j++) {
            for(int k = maxheavy; k >= stones[j]; k--) {
                dp[k] = max(dp[k], dp[k - stones[j]] + stones[j]);
            }
        }
        int res = (sum - dp[maxheavy]) - dp[maxheavy];
        return res;
    }
};

// 代码随想录版本
class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        vector<int> dp(15001, 0);
        int sum = 0;
        for (int i = 0; i < stones.size(); i++) sum += stones[i];
        int target = sum / 2;
        for (int i = 0; i < stones.size(); i++) { // 遍历物品
            for (int j = target; j >= stones[i]; j--) { // 遍历背包
                dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - dp[target] - dp[target];
    }
};