118. 杨辉三角 - 力扣

题目链接：118. 杨辉三角 - 力扣（LeetCode）

题目内容：

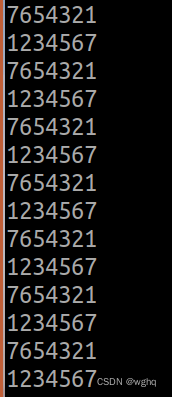
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:
输入: numRows = 1
输出: [[1]]

思路

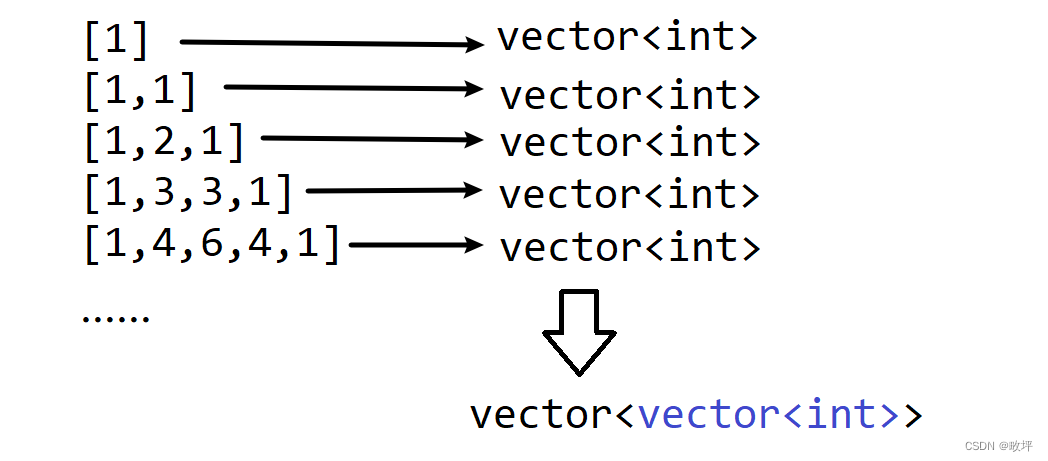
在这里插入图片描述

解：

class Solution {
public:
    vector<vector<int>> generate(int numRows) 
    {
        vector<vector<int>> vv;
        vv.resize(numRows,vector<int>());
        for(int i = 0;i < numRows;++i)
        {
            vv[i].resize(i+1,0);
            vv[i][0] = vv[i][vv[i].size()-1] = 1;
            for(int j = 1;j < vv[i].size()-1;++j)
            {
                vv[i][j]=vv[i-1][j-1]+vv[i-1][j];
            }
        }
        return vv;
    }
};

17. 电话号码的字母组合 - 力扣

题目链接：17. 电话号码的字母组合 - 力扣（LeetCode）

题目内容：

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：
输入：digits = ""
输出：[]

示例 3：
输入：digits = "2"
输出：["a","b","c"]

思路：递归

示例：
若 string digits = "234"
则如下图：

解：

class Solution {
    vector<string> DigitToAlphet = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
    void Combinations(const string& digits,size_t di,string combination,vector<string>& ret)
    //combination用来存储每层递归后，最终得到的一个组合的string
    //di是用来标识string digits中的数字读到第几个
    {
        if(di==digits.size())
        {
            ret.push_back(combination);
            return;
        }
        int num = digits[di] - '0';
        for(auto e:DigitToAlphet[num])
        {
            Combinations(digits,di+1,combination+e,ret);
        }
    } 

    vector<string> letterCombinations(string digits) 
    {
        vector<string> ret;
        if(!digits.empty())
            Combinations(digits,0,"",ret);
        return ret;
    }
};

137. 只出现一次的数字 II- 力扣

题目链接：137. 只出现一次的数字 II- 力扣（LeetCode）

题目内容：

给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现三次。请你找出并返回那个只出现了一次的元素。

注意：你必须设计并实现线性时间复杂度的算法且不使用额外空间来解决此问题。

示例 1：
输入：nums = [2,2,3,2]
输出：3

示例 2：
输入：nums = [0,1,0,1,0,1,99]
输出：99

思路：

文字版详细思路见力扣官方题解。

下图为官方题解中的方法二的图解。
在这里插入图片描述

解：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret=0;
        for(int i=0;i<32;++i)
        {
            int sum=0;
            for(auto e:nums)
            {
                sum += ((e>>i)&1);
            }
            if(sum%3)
                ret |= (1<<i);
        }
        return ret;
    }
};