本节课主要介绍了Batch和Momentum这两个在训练神经网络时用到的小技巧。合理使用batch,可加速模型训练的时间,并使模型在训练集或测试集上有更好的表现。而合理使用momentum,则可有效对抗critical point。
课程视频:
Youtube:https://www.youtube.com/watch?v=zzbr1h9sF54
知乎:https://www.zhihu.com/zvideo/1617121300702498816
课程PPT:
https://view.officeapps.live.com/op/view.aspx?src=https%3A%2F%2Fspeech.ee.ntu.edu.tw%2F~hylee%2Fml%2Fml2021-course-data%2Fsmall-gradient-v7.pptx&wdOrigin=BROWSELINK
一、Batch
在optimization的过程中,我们实际算微分的时候并不是对所有的data做微分,而是将data分为一个一个的batch (mini batch) 计算微分。
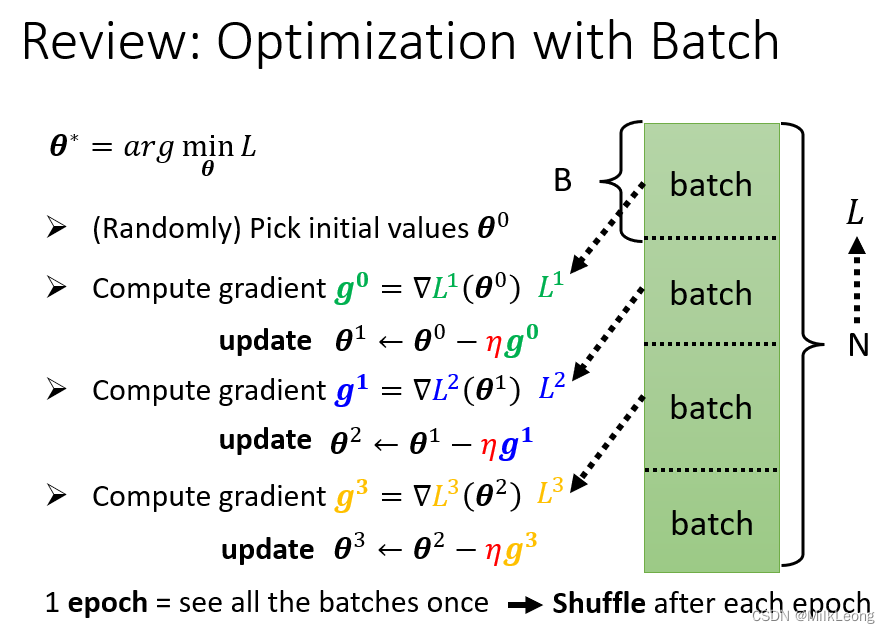
例如上图,程序先使用第一个batch的数据计算Loss L1,再用L1计算gradient g0,并使用g0来update参数(θ0→θ1);之后,程序又使用第二个batch计算Loss L2,再用L2计算gradient g1,并使用g1来update参数(θ1→θ2)。当所有的batch都过完一遍后,我们就说过完了一个epoch。
shuffle是与epoch相关的另一个概念。在每一个epoch开始之前我们都会将其分为一个个batch,shuffle的作用就是确保每一个epoch的batch都不一样。
batch的大小对训练的过程和结果都有一定的影响。如下图,假设一个数据集中有N个样例,左边的batch size = N,即full batch,相当于没有使用batch,程序一次遍历完所有的样例后才update参数;右边的batch size = 1,可视为small batch,程序遍历一个样例即更新一次参数,在一个epoch里需要更新N次参数。从图中看,当batch size = 1时,由于每次只根据一个样例来计算loss,它求出来的gradient噪声是比较大的,所以update的方向看上去是曲曲折折;而左边是根据所有样例来计算loss,其参数的update看上去更为稳健。

small batch和large batch之间的差异,具体还可从以下几个维度来看:
1. Smaller batch requires longer time for one epoch
如果不考虑并行运算,large batch在训练的过程中,一次需要读更多的数据,它所花费的时间应该比small batch的时间长。但是时间上GPU一般都有并行运算的能力,它可以同时处理多笔数据。当batch size在一定的阈值,训练完一个batch,large batch所花费的时间并不一定比small batch所需的时间多 (如下图左边所示)。相反,在一个epoch中,batch size越小,update参数的次数就越多,训练花费的时间也就更久 (如下图右边所示)。
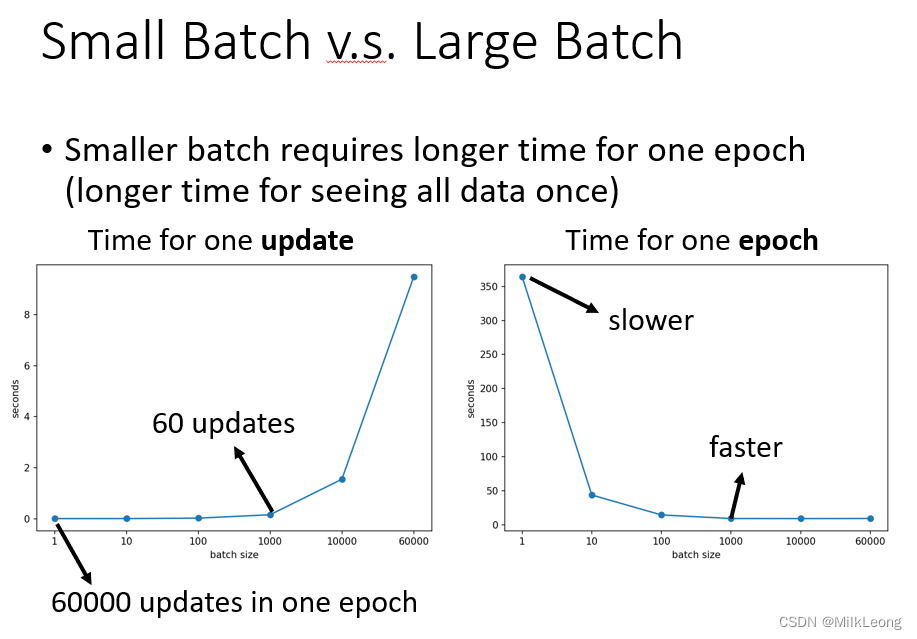
2. Smaller batch size has better performance
有实验表明,small batch在训练时取得的准确率更高,从下图可以看出,不管是在训练集还是验证集上,随着batch size增大,模型的准确率会降低。
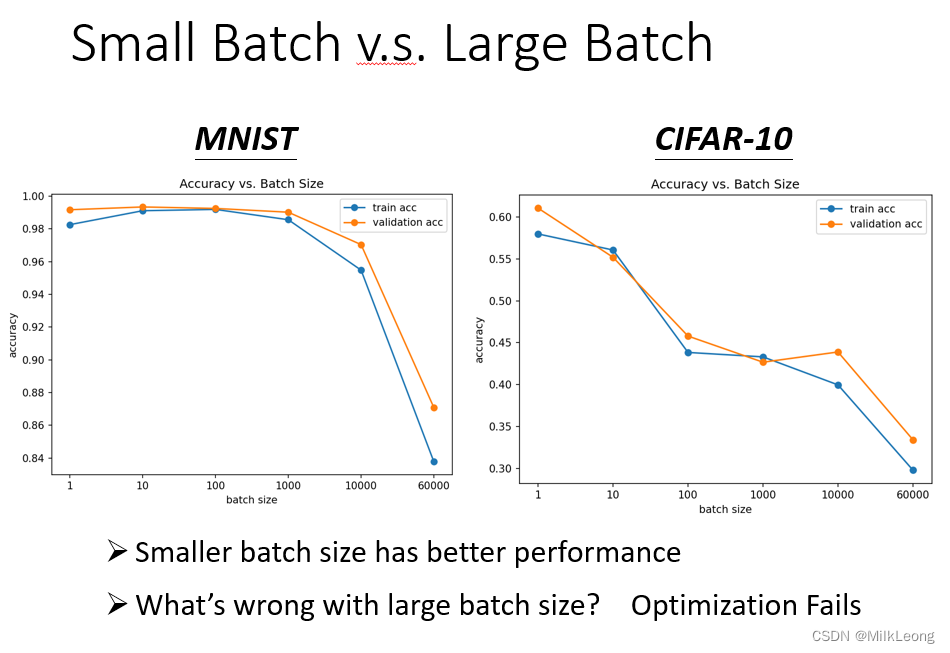
对此的一种解释是,large batch更容易陷入critical point。如下图,左边的full batch如果卡在了gradient为0的点,那么update就会停在这个点;而邮编的samll batch,如果一笔batch卡在这个点,可以接着用另一笔来计算loss,或许可由此跳出critical point。
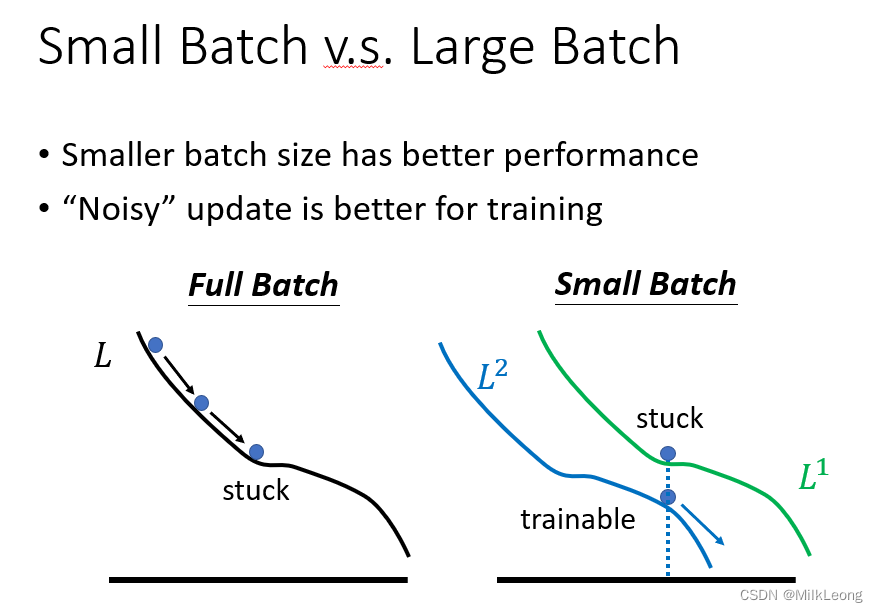
3. Small batch is better on testing data
有研究表明,在测试集上使用small batch得到的准确率可能更高。如下图所示,尽管在测试集上可能有的large batch的准确率可能略高于small batch,但在测试集上small batch的准确率无一例外均高于large batch。
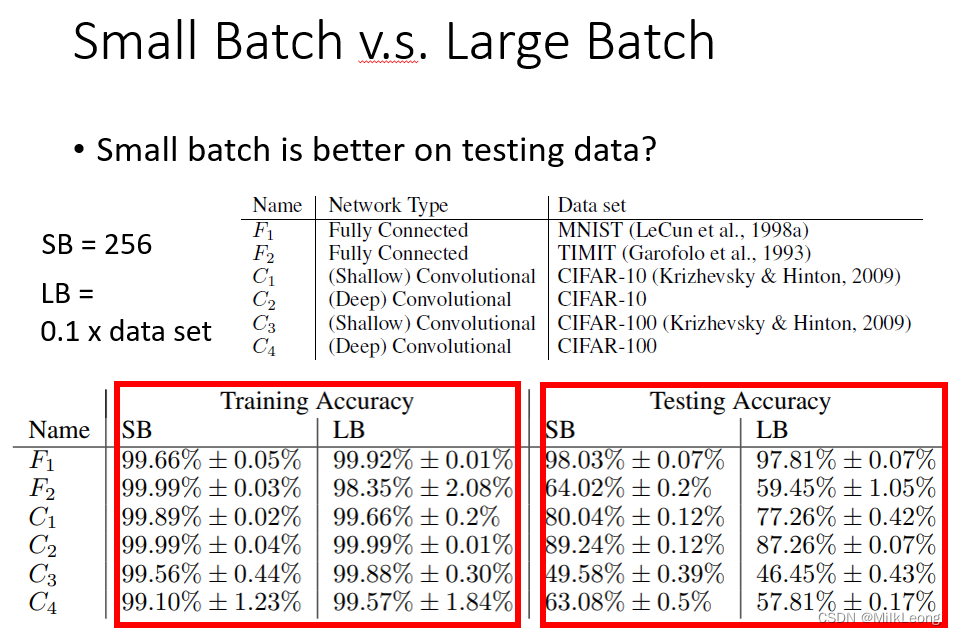
一种可能的解释是,窄的峡谷没有办法困住small batch,而大的平原才有可能困住small size,而large batch则容易被困在峡谷里。从下图中可以看出,如果是在峡谷,训练集上的Loss和测试集上的Loss差距较大,从而导致准确率变低。
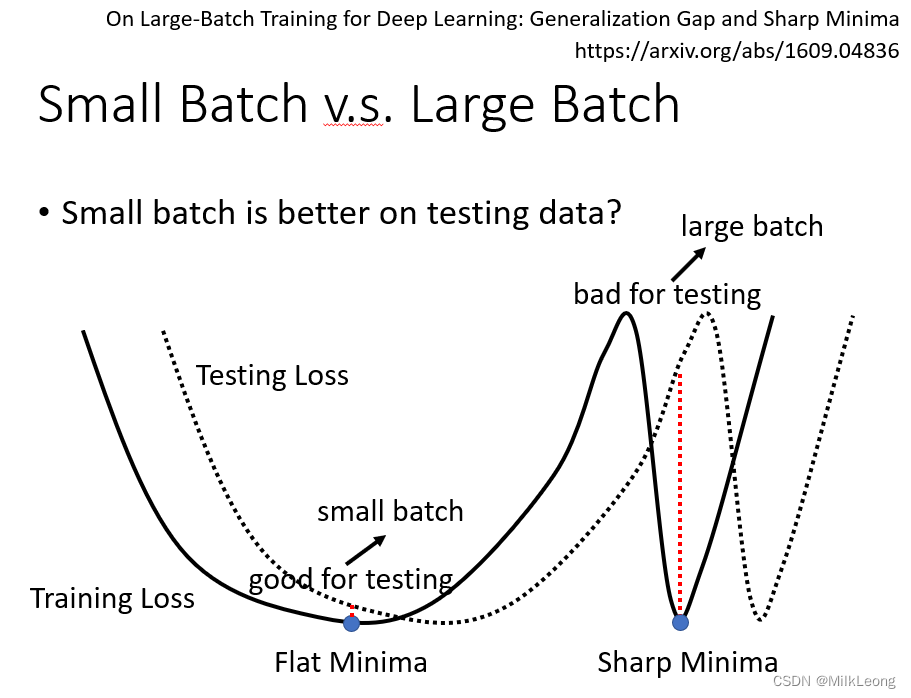
总的来说,small size和large size之间的对比如下:
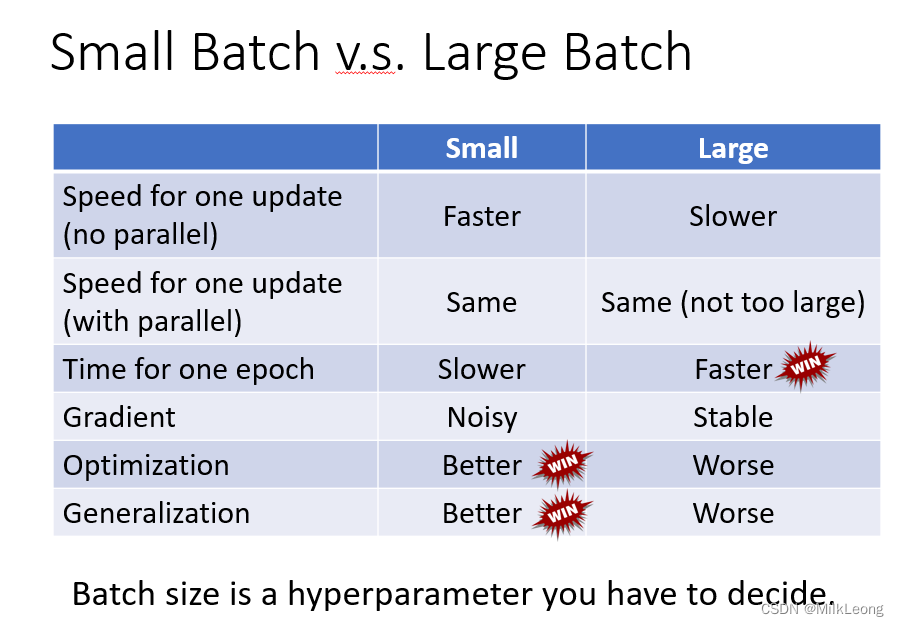
二、Momemtum
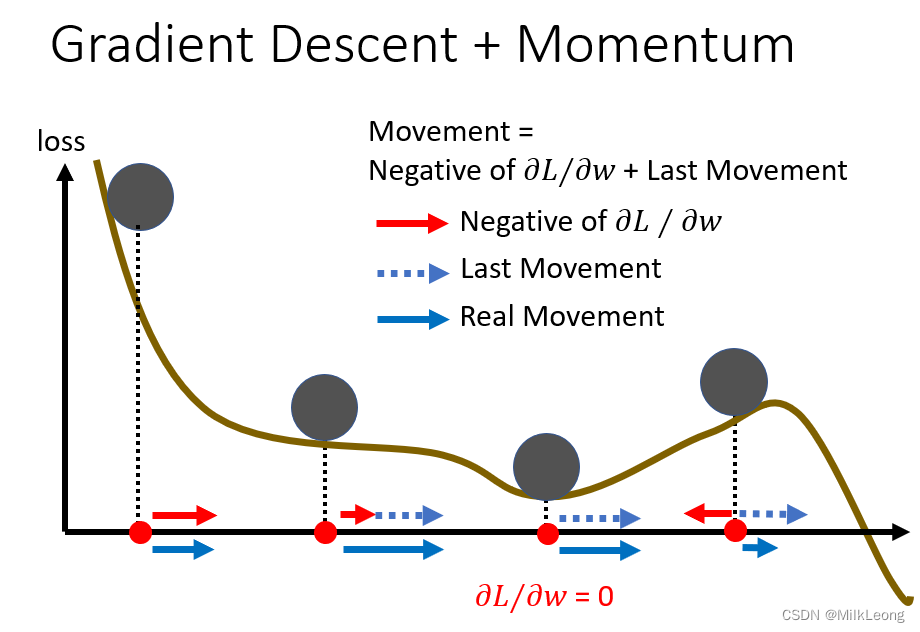
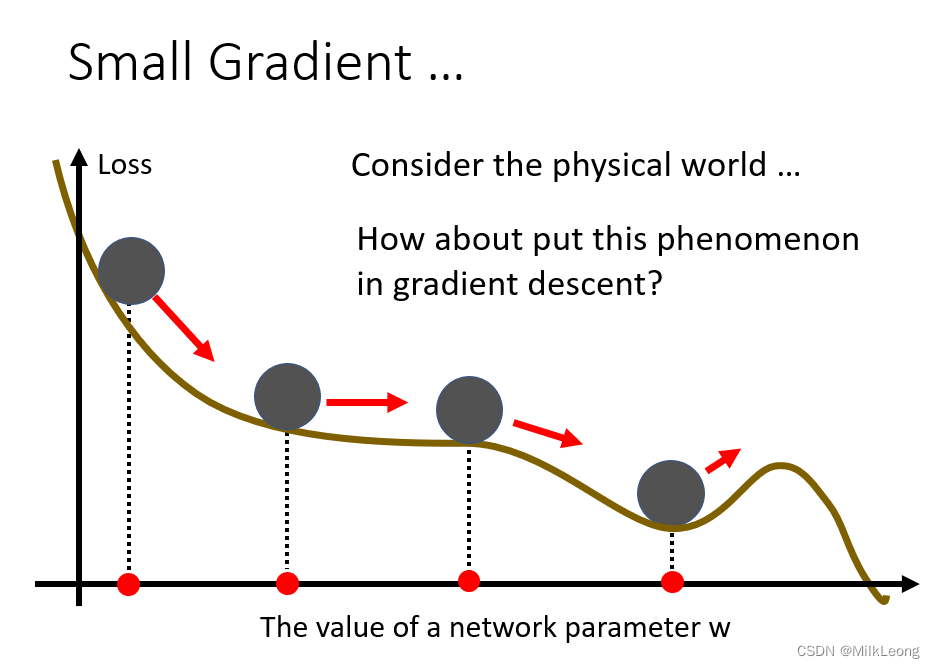
momentum是另一个可能对抗critical point的技术。
如下图,我们假设error surface是一个斜坡,而参数是一个球,在现实的物理时间中,球从斜坡上滚下,不一定会被saddle point或local minima卡住,因为惯性在起作用,受惯性影响,即便受到阻力,球仍然会在一定的时间段内保持原来的运动状态。momentum在训练神经网络过程中的作用就相当于物理世界的惯性。
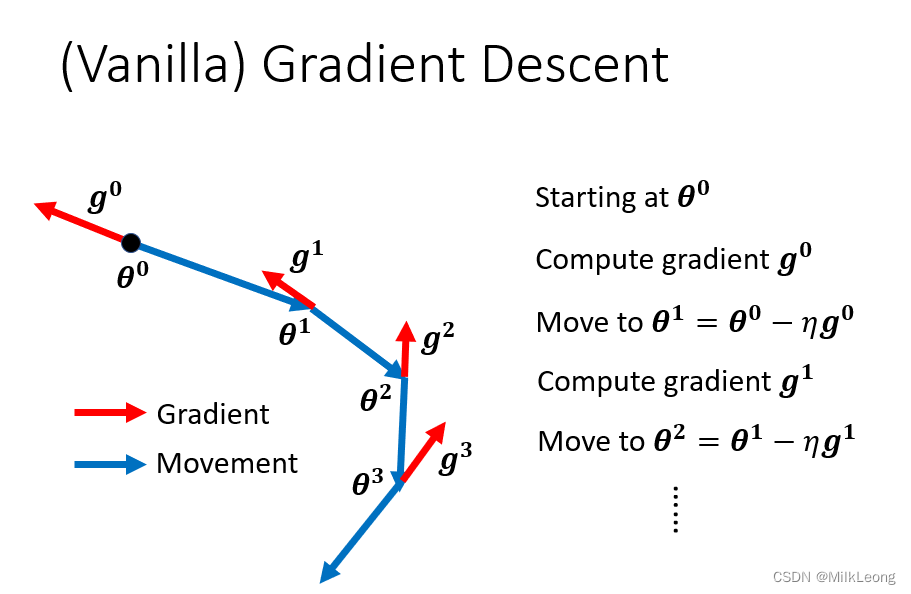
下图是一个一般的(Vanilla)使用梯度下降法的过程(不考虑momentum)。我们先计算梯度g,再沿着梯度的反方向移动以更新θ。
而如果考虑momentum,整个梯度下降法更新参数 θ 的过程则如下。第 i 次update时的momentum mi,其方向与上一次参数更新的movement方向一致(如图中蓝色虚线所示)。如果考虑momentum,在第 i 次update参数 θ 时,会综合梯度 gi的反方向(如图中红色虚线所示)与mi(前一步移动的方向),来选择本次move的方向(如图中蓝色实线所示)。
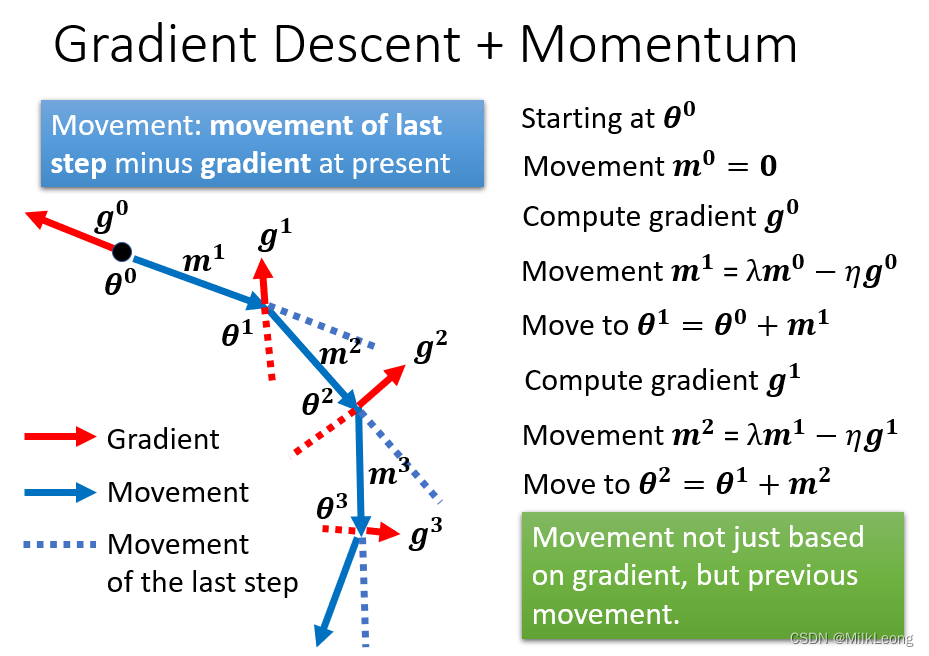
从下图中左侧的公式推导过程可知,momentum mi其实可以看做之前之间计算出来的gradient的weighted sum。因而我们可以说,加上momentum后的uodate不是只考虑当前的gradient,而是考虑过去所有的gradient的总和。