513. 找树左下角的值
文章目录
- [513. 找树左下角的值](https://leetcode.cn/problems/find-bottom-left-tree-value/)
- 一、题目
- 二、题解
- 方法一:递归法(层序遍历,深度优先搜索)
- **不足之处以及如何改进**
- 方法二:迭代
一、题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
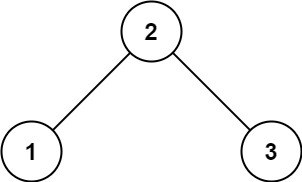
输入: root = [2,1,3]
输出: 1
示例 2:
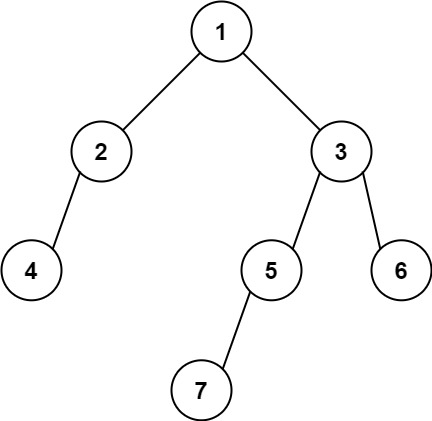
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
二、题解
方法一:递归法(层序遍历,深度优先搜索)
我们可以使用递归来进行深度优先搜索,将每一层的节点值按照层级存储在一个二维向量中,最后返回最底层最左边的节点值。
算法思路:
- 使用深度优先搜索(DFS)来遍历整个二叉树。
- 在遍历的过程中,我们需要记录每个节点所在的层级,然后将节点值存储在对应的层级中。
- 为了达到这个目的,我们可以使用一个二维向量
result,其中result[i]存储第i层的节点值。 - 我们定义一个辅助函数
find,接受三个参数:vec用来存储节点值,node当前处理的节点,depth当前节点的深度。 - 在
find函数中,我们首先检查当前节点是否为空,如果是,则直接返回。 - 如果
depth等于vec的大小,说明当前层级还没有被记录,因此需要在vec中添加一个新的空向量。 - 将当前节点值加入到
vec[depth]中,然后递归处理左子树和右子树,将深度加一传递下去。 - 在主函数
findBottomLeftValue中,我们首先创建一个空的二维向量result。 - 调用
find函数来遍历二叉树并填充result。 - 返回
result最底层最左边的节点值,即result[result.size() - 1][0]。
具体实现:
class Solution {
public:
void find(vector<vector<int>>& vec, TreeNode* node, int depth) {
if (node == nullptr) {
return;
}
if (depth == vec.size()) {
vec.push_back(vector<int>());
}
vec[depth].push_back(node->val);
find(vec, node->left, depth + 1);
find(vec, node->right, depth + 1);
}
int findBottomLeftValue(TreeNode* root) {
vector<vector<int>> result;
find(result, root, 0);
return result[result.size() - 1][0];
}
};
算法分析:
- 时间复杂度:遍历整个二叉树的时间复杂度为 O(N),其中 N 是二叉树的节点数。在每个节点上,我们进行常数时间的判断、添加和递归操作。
- 空间复杂度:递归函数的调用会占用栈空间,递归的深度最坏情况下为树的高度,所以空间复杂度为 O(H),其中 H 是二叉树的高度。在最坏情况下,二叉树可能退化为链表,高度为 N,此时空间复杂度为 O(N)。但在一般情况下,二叉树的高度平衡,空间复杂度会接近 O(logN)。
不足之处以及如何改进
上面这个算法在递归过程中对左子树和右子树都会调用 findLeftMostValue 函数,即使在左子树的递归中已经找到了最底层最左边节点,仍然会递归处理右子树。这会导致不必要的重复计算。
改进版算法通过在递归中记录已找到的最大深度 maxDepth,只在当前深度大于最大深度时才更新 result 和 maxDepth。这样,如果我们在某一层已经找到了最底层最左边的节点,就不会再继续递归处理右子树,从而减少了不必要的递归操作。
改进版本
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
int depth = 0; // 记录当前节点的深度
int result = 0; // 记录最底层最左边节点的值
findLeftMostValue(root, 1, depth, result);
return result;
}
void findLeftMostValue(TreeNode* node, int currentDepth, int& maxDepth, int& result) {
if (!node) {
return;
}
//这里进行了改良,当深度发生变化时result也发生变化,直到最底层
if (currentDepth > maxDepth) {
result = node->val;
maxDepth = currentDepth;
}
findLeftMostValue(node->left, currentDepth + 1, maxDepth, result);
findLeftMostValue(node->right, currentDepth + 1, maxDepth, result);
}
};
方法二:迭代
算法思路:
我们也可以使用队列来进行广度优先搜索,逐层遍历二叉树。具体的算法思路如下:
- 我们首先创建一个空队列
que,用来存储待处理的节点。 - 如果根节点
root不为空,我们将根节点入队列。 - 我们定义一个变量
result来记录最底层最左边节点的值,初始值设为 0。 - 开始循环处理队列中的节点,直到队列为空。
- 在每一层遍历中,我们首先获取当前队列的大小
size,即当前层的节点个数。 - 然后,我们使用一个循环来处理当前层的所有节点:
- 弹出队首节点
node,如果是当前层的第一个节点(即i == 0),我们将其值赋给result。 - 如果
node的左子节点不为空,将左子节点入队列。 - 如果
node的右子节点不为空,将右子节点入队列。
- 弹出队首节点
- 当队列为空时,循环结束,此时
result中存储的就是最底层最左边节点的值,我们将其返回。
具体实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if (root) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (i == 0) {
result = node->val; // 记录最后一行第一个元素
}
if (node->left) {
que.push(node->left);
}
if (node->right) {
que.push(node->right);
}
}
}
return result;
}
};
算法分析:
- 时间复杂度:遍历整个二叉树的时间复杂度为 O(N),其中 N 是二叉树的节点数。在每个节点上,我们进行常数时间的判断、入队和出队操作。
- 空间复杂度:队列
que会占用额外的空间,其大小不会超过二叉树的宽度,因此空间复杂度为 O(W),其中 W 是二叉树的宽度,最坏情况下会达到 O(N)。在一般情况下,二叉树的宽度较小,空间复杂度会接近 O(1)。