基于Jonswap谱的随机波高及波压力生成

海面高程可视为是平稳高斯随机过程，可通过对波浪谱确定的一系列分量波进行叠加得到。JONSWAP谱是在海洋结构设计和分析中常用的波浪频谱，可以用其来模拟随机波浪。
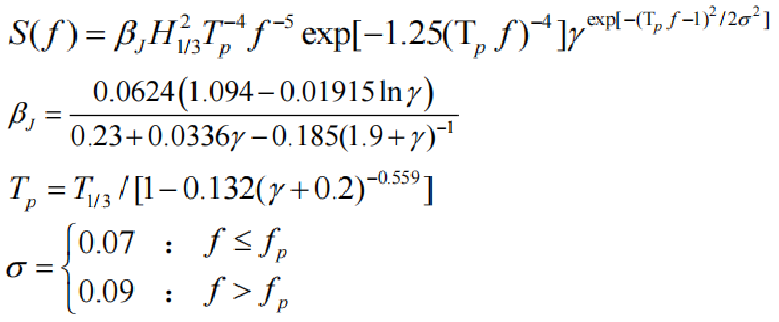
在这里插入图片描述
式中：有义波高H1/3和有义周期T1/3，T p 为频谱峰值点对应的波浪周期，fp为峰值频率，γ 是谱峰升高因子，取 3.3。

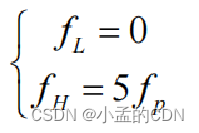
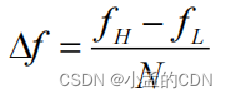
在这里插入图片描述

N为谱分量数目

海床示意图 ## 1.1 不同位置处的随机波高时间序列代码如下：

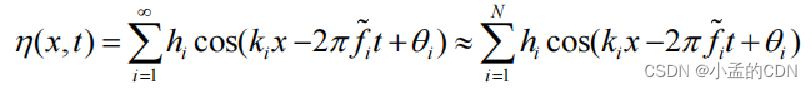
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family']='Times new roman'
plt.rcParams['font.size']=20
plt.rcParams['mathtext.fontset'] = 'stix'
np.random.seed(1)
N=500;T31=10;H31=6;gamma=3.3;
Tp=T31/(1-0.132*(gamma+0.2)**(-0.559))
fp=1/Tp
fL=0.01;fH=5*fp;d=25
delatf=(fH-fL)/N
f=np.arange(fL,fH,delatf)
def sigma(f,fp):
    sigma=np.piecewise(f,[f<=fp,f>fp],[0.07,0.09])
    return sigma
def k_solve(f,d):   
    T=1/f
    mu0=(2*np.pi)**2*d/(9.8*T**2)
    mu=mu0*(1+mu0*np.exp(-(1.835+1.225*mu0**1.35)))/np.sqrt(np.tanh(mu0))
    k=(2*np.pi)/(2*np.pi*d/mu)
    return k
betaJ=0.0624*(1.094-0.01915*np.log(gamma))/(0.23+0.0336*gamma-0.185*(1.9