一、索引的数据结构🌸

索引的数据结构（非常重要）

mysql的索引的数据结构，并非定式！！！取决于MySQL使用哪个存储引擎

数据库这块组织数据使用的数据结构是在硬盘上的。我们平时写的代码是存在内存里面，内存里面的数据结构，对于访问操作不敏感，（找数据的过程花费的时间多，但是真正用于访问的数据不多，硬盘上的数据操作，对于访问操作比较敏感，但是⚠️读写一个的硬盘

开销是远大于内存的，读写一次硬盘，差不多可以多些一万次内存了。 

数据结构简单回顾，引入innodb💘💘💘 

MySQL包含很多模块，

有的解析SQL，有的用于网络通信，有的存储数据结构->如：存储引擎，本质上就是代码中的一个模块（这里包含若干个代码文件····以及一大堆具体的代码）

✨✨✨最主流的存储引擎：innodb

索引用的数据结构我们也只介绍innodb

我们要先知道索引是为了查找！！！（查找快的才牛波一）

让我们简单的回顾一下数据结构的知识吧 （🌝 🌚 🌑正好学的次）

顺序表：尾插，随机访问很屌

链表：中间位置的插入删除很屌

栈和队列：特定位置的增删查改

二叉树->二叉搜索树->平衡机制的二叉树（红黑树）或许可以查找速度还是很屌的

堆：适合排序，找最大最小

哈希表：查找嘎嘎🐮牛波一（以后工作常用）

 👲 👳 👷

那来看看哪个更适合呢 

红黑树：插入，删除，修改，查询，-元素有序，可以处理范围查询

最大问题，红黑树会在元素比较多的时候变的很高->对应比较次数就会变得很多，每次比较都意味着硬盘IO操作！！！（很耗硬盘开销）

单单这几个数，他就已经树高变成这样了

哈希表：哈希表的问题是只可以精准查询，不能支持模糊查询，范围查询（哈希表需要通过给定的key，通过hash函数映射出一个具体下标，才能定位到具体位置）。

二、B树💓💓💓

那么索引（innodb引擎)到是用的什么数据结构呢？

为了数据库，大佬们专门搞了个数据结构叫B+树（其他存储引擎中可能用到hash（哈希表）作为索引->只能应对这种精准匹配自己的情况了

那么什么是B+树呢，那我们需要了解B树也叫（B-树。叫B杠树 不要当土狗😨）

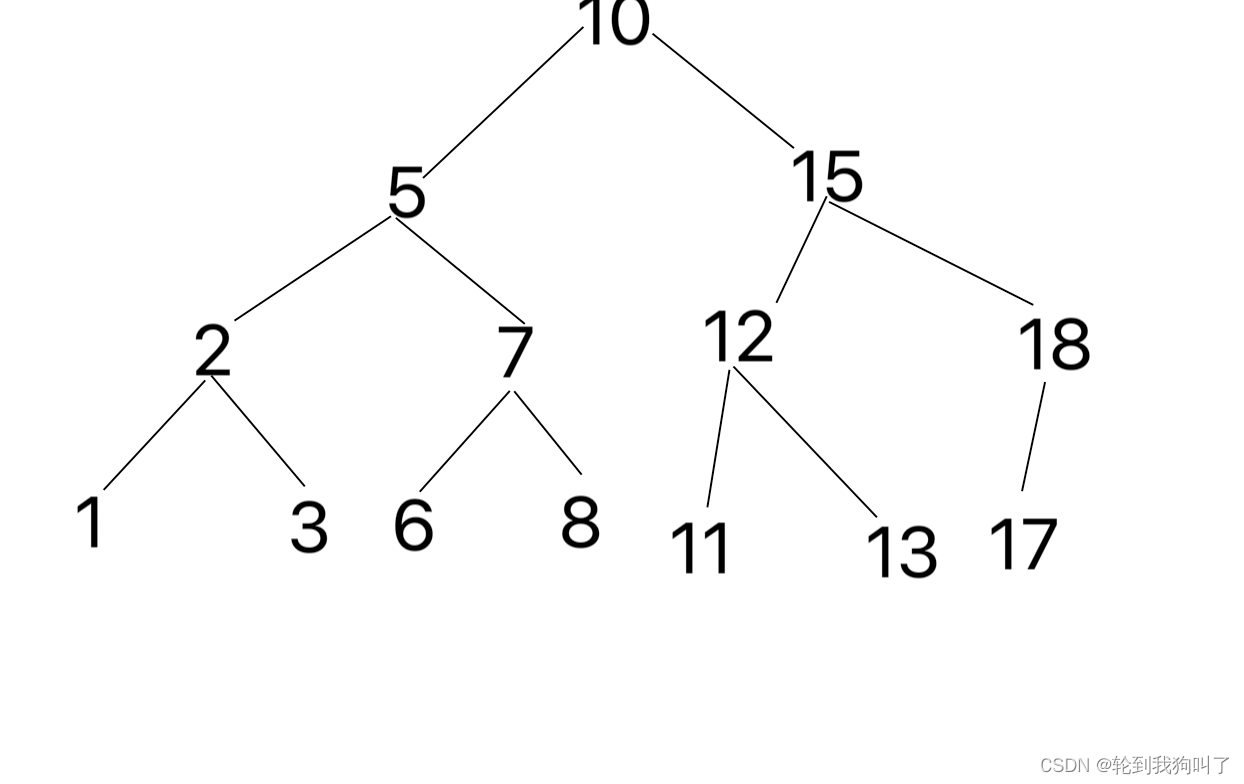
B树的本质是一个N叉搜索树，一个节点可以保存多个key，N个key就可以延伸出n+1个分叉来，N个key划分出了N+1个空间，（4个数5个空间）如下图

注意：一个节点多个key和一个key 都差不多的硬盘开销 

此时每个节点上，都可以保存多个元素，当总的元素个数固定时，相较于二叉搜索树，涉及到的节点总数大大降低，树高也大大降低了，B树和B+树高度远远小于红黑树，于是这么查询，硬盘的IO次数也就随之减少了。

对于B树插入和删除元素，就涉及拆封和合并的操作（比如，拆分是确认区间，合并是给他聚到一起）当然了一个节点也不可以无脑存key（就是数），要不然存的太多就要变成数组了，所以要把这个节点一部分key以树节点的方式重新组织。

如1，2，3，4，此时再加入个5，就有点多了，所以说此时就会把 1，2，3，4，5

拆分成如下图，保持当前节点的key始终不会太多，此时就会生出新的叶节点

B树不如B+树的一个点：B+树全集有叶子和非叶子，如果写元素存到每一个节点上，非叶节点占据空间比较大，从而无法从内存中缓存了。

补充一个小知识点（HashMap负载因子是多少 ‘0.75’，链表长度多少时候转化为红黑树 ‘8’ 但是首先HashMap不是哈希表，只是哈希表的一种表达方式，但是最好不要记参数，最好要根据实际情况。 

 三、B+树💚 💚 💚 

B+树在B树的情况下，又做出了一些改进->针对数据库的场景展开的

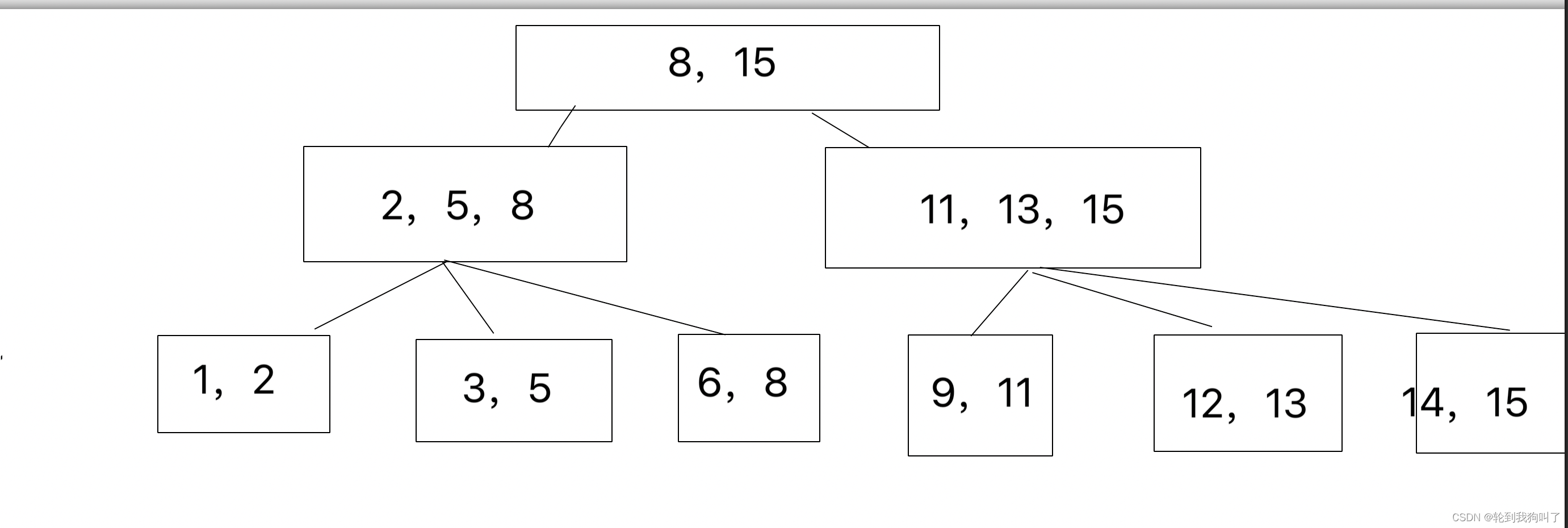
1.B+也是二叉搜索树，但是N个key分出了N个区间，其中最后一个就是相当于最大值 

2.父节点的key在子节点重复出现（而且是以最大值的身份）

看起来会有很多的元素，浪费空间，但实际上可以起到非常重要的作用（上面存在的，下面都有，叶子节点这一层，包含了整个数据的全集！）

3.把叶子节点，按照链表方式首尾相连，此时可以通过叶子节点之间的连接，快速找到上一个/下一个的元素）

 

  四、B+树的优点产生的优势💞

1.特别擅长范围查询             

2.所有的查询操作最终都会落在叶子节点，比较次数，是均衡的，查询时间是稳定的，还是那句话‘有时候稳定比快更好’，时快时慢，用户的体验会不好，慢点但是稳定才好。

3.在B+树中，叶子节点上是完整的数据全集（注意哈，1不是只代表1，而是代表ID为1的连接。如同 1 -张三-90分），因此表中的每一个数据的其他列都可以得到在叶子节点上，只存储构建索引的id就行（就相当于一个网址链接）

物理层面：不需要表格这样的数据结构，直接使用B+树来存储这个表的数据，‘表格’只是用户看起来这个像是个表格而已，此时，非叶子节点的存储空间消耗是非常小的！！！（叶子存在硬盘，非叶子可以存在内存中），此时，进行数据查询的时候，就可以通过内存来直接比较，从而更快速的找到叶子节点上的记录（进一步又减少了硬盘IO的次数）

---

五、事务的基本情况💖

什么叫事务呢？

假如说表balance(accountId,balance)

                                       1     ,   1000

                                       2     ,  1000

1号给2号转账500，分为两步，第一步给1账户扣500，给2账户+500，中间还不能有差错，不然用户脑袋气死了😡

执行的时候，肯定是不知道哪一步会失败，❗️❗️然后事务的本质是把多个操作，打包成一个操作完成的，让这个操作，要不我就全部完成，要不我就完全失败那种——原子性😃😃

⚠️⚠️完全失败不是说一个没做，而是说假如第一步做了，但是第二步失败了，他的选择是把第一步给还原回去。（这个还原我们也管他叫回滚）

如何实现回滚呢：只要把事务中执行的每个操作都记录下来（通过特定的日志，来记录数据库事务操作的中间过程），如果需要回滚，按照之前的操作的“逆操作”就可以了。

如：1号-500，2号+500  

若执行第一步的过程中，如果程序崩溃了～此时，就要对第一步进行回滚～～

数据库会自动把第一步操作的修改还原回去，那么假如数据库挂了呢🌚重启了捏🌚

我们是通过日志，来记录事务执行的中间过程的，日志中的数据始终在硬盘上存在的。即便是数据库服务器重启～就会在启动之后，针对之前没回滚完成的情况，继续处理～

要么是全部成功，要么是一个都不执行。

事务->原子性->回顾->特定日志

六、事务的使用方式💘

开启事务：start transaction  （下面就可以输入多个sql语句了 ）

提交事务：commit。     （把这些SQL按照原子的方式进行执行）

手动出发回滚：rollback  手动触发回滚～～

一个事务务必以后两条操作结尾(当然了解命令即可，不会用这个命令，我们一般是使用代码去操作事务)

 

 七、事务的基本特性（面试题，理解的去思考去记）💜 💜 💜 

1.原子性：保证多个操作被打包成一个整体，要不全成，要不一个也不做。

2.一致性：事务执行之前，和事务执行之后，数据能对上，数据不能够太牛马离谱

3.持久性；事务这里的各种操作，都是持久生效最终写到硬盘上，即使关机，也不影响的

4.隔离性：并发执行事务时候，隔离性，会在执行效率和数据可靠之间做出权衡，隔离描述的是在同时执行的事务之间，相互的影响，隔离性越高，并发性越低，数据越可靠，性能也就越低。（下一篇会介绍并发的，家人们别急）