假设检验的两种原假设取舍决定方式
在t检验,相关分析,回归分析,方差分析,卡方检验等等分析方法中,都需要用到假设检验。假设检验的步骤一般如下:
- 提出假设:H0 vs H1 ;
- 假设原假设H0 成立的情况下,计算一个统计量;
- 在统计分布表中查找临界值,在t检验中,如果确定置信度为 0.05 的话,那么临界值为 t0.05
- 比较临界值和统计量的大小,决定是否接受原假设。如果选择接受原假设,那么原假设 H0 成立;如果选择拒绝原假设,那么备择假设 H1 成立。
通过一张图我们来梳理一下:
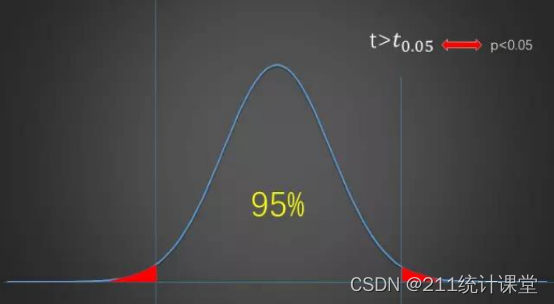
我们先假定原假设是成立的,这样正常情况之下,计算的统计量应该是落在两根线之间的区域的,而如果计算的统计量超出了这个区域,那么说明原假设是有问题的。这里利用了小概率原理:概率很小的事情,在一次试验中,一般不会发生,如果你买过彩票,应该很容易理解这句话。对应于图中就是,红色部分的数值出现的概率很小,出现了就不正常,就要否定原假设,接受备择假设。
现在我们来看,两根线与横轴相交的地方,是一个数值,统计量小于这个数值的绝对值(说绝对值是因为两边都有线),那么统计量就落在中间的 95% 区域中(这个区域也称为接受域),反之则落在外面红色部分的 5% 的区域中。
第一种判断方法就是,用计算的统计量和两个临界值(两根线的位置)比较,如果超出,则拒绝原假设。
第二种方法,如果一个统计量要落在两根线的两边,概率是多少呢,是 0.05,如果再往两边靠呢,那就小于 0.05 了。所以当概率值 p 小于 0.05 时,统计量也超出 95% 的区域了,也要拒绝原假设。
这两种方法本质是一样的,但是一般我们在学校学习计算时,是用前一种方法来判断,而统计软件给出的是第二种判断方法。有的人就不太明白了。本文对该问题的两种不同方式进行了区分,帮助大家认识到其共通之处。