1案例背景

1.1离散Hopfield神经网络概述

        Hopfield网络作为一种全连接型的神经网络,曾经为人工神经网络的发展开辟了新的研究途径。它利用与阶层型神经网络不同的结构特征和学习方法,模拟生物神经网络的记忆机理,获得了令人满意的结果。这一网络及学习算法最初是由美国物理学家J.JHopfield于1982年首先提出的,故称为Hopfield神经网络。
        Hopfield最早提出的网络是二值神经网络,神经元的输出只取1和一1,所以,也称离散Hopfield神经网络(Discrete Hopfield Neural Network, DHNN)。在离散Hopfield网络中，所采用的神经元是二值神经元,因此,所输出的离散值1和一1分别表示神经元处于激活和抑制状态。
        1．网络结构
        DHNN是一种单层、输出为二值的反馈网络。由三个神经元组成的离散 Hopfield神经网络的结构如图9-1所示。

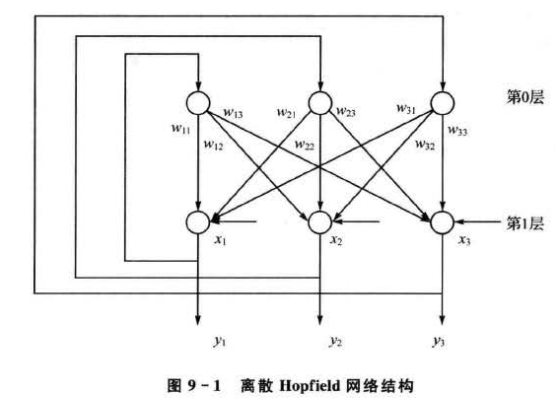
在图9-1中,第0层仅仅作为网络的输入,它不是实际神经元,所以无计算功能;第1层是神经元,故而执行对输人信息与权系数的乘积求累加和,并经非线性函数f处理后产生输出信息。f是一个简单的阙值函数,如果神经元的输出信息大于阈值θ,那么,神经元的输出取值为1;小于阈值0,则神经元的输出取值为—1。对于二值神经元,它的计算公式如下:

2．网络工作方式
        Hopfield网络按动力学方式运行,其工作过程为神经元状态的演化过程,即从初始状态按“能量”(Lyapunov函数)减小的方向进行演化,直到达到稳定状态,稳定状态即为网络的输出。
Hopfield网络的工作方式主要有两种形式:
        ①串行(异步)工作方式。在任一时刻t,只有某一神经元ü(随机的或确定的选择)依式(9-4)与式(9-5)变化,而其他神经元的状态不变。
②并行(同步)工作方式。在任一时刻t,部分神经元或全部神经元的状态同时改变。下面以串行(异步)工作方式为例说明Hopfield网络的运行步骤:
        步骤1:对网络进行初始化。
        步骤2:从网络中随机选取一个神经元i。步骤3:计算该神经元主的输入ui(t)。
        步骤4:计算该神经元i的输出v;(t＋1),此时网络中其他神经元的输出保持不变。
        步骤5:判断网络是否达到稳定状态,若达到稳定状态或满足给定条件则结束;否则转到步骤2继续运行。
        这里网络的稳定状态定义为;若网络从某一时刻以后,状态不再发生变化,则称网络处于稳定状态。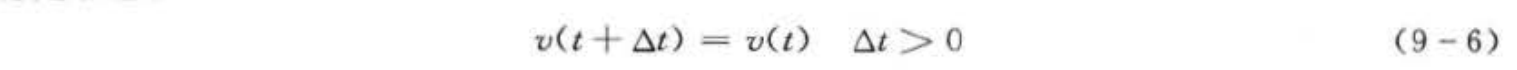

        3．网络稳定性
        从 DHNN的结构可以看出:它是一种多输人,含有阈值的二值非线性动态系统。在动态系统中,平衡稳定状态可以理解为系统某种形式的能量函数在系统运动过程中,其能量值不断减小,最后处于最小值。
        Coben和 Grossberg在1983年给出了关于 Hopfield网络稳定的充分条件,他们指出:如果 Hopfield网络的权系数矩阵W是一个对称矩阵,并且对角线元素为0,则这个网络是稳定的。即在权系数矩阵W中,如果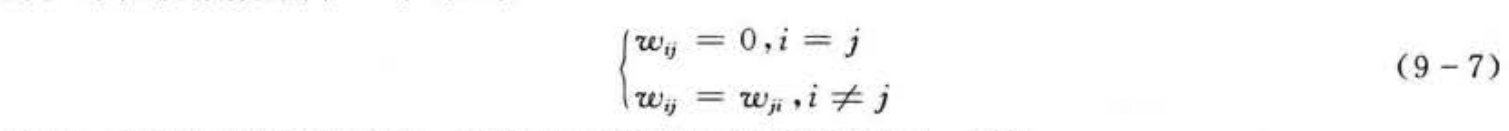

        则Hopfield网络是稳定的。详细推导过程见参考文献[1]～~[3]。
        应该指出,这只是 Hopfield网络稳定的充分条件,而不是必要条件。在实际中有很多稳定的Hopfield网络,但是它们并不满足权系数矩阵W是对称矩阵这一条件。

1.2数字识别概述

在日常生活中,经常会遇到带噪声字符的识别问题,如交通系统中汽车车号和汽车牌照，由于汽车在使用过程中,要经受自然环境的风吹日晒,造成字体模糊不清,难以辨认。如何从这些残缺不全的字符中攫取完整的信息,是字符识别的关键问题。作为字符识别的组成部分之一,数字识别在邮政、交通及商业票据管理方面有着极高的应用价值。
目前有很多种方法用于字符识别,主要分为神经网络识别,概率统计识别和模糊识别等。传统的数字识别方法在有干扰的情况下不能很好地对数字进行识别,而离散型Hopfield神经网络具有联想记忆的功能,利用这一功能对数字进行识别可以取得令人满意的效果,并且计算的收敛速度很快。

1.3 问题描述

根据Hopfield神经网络相关知识,设计一个具有联想记忆功能的离散型Hopfield神经网络。要求该网络可以正确地识别0~9这10个数字,当数字被一定的噪声干扰后,仍具有较好的识别效果。

2模型建立

2.1设计思路

假设网络由0~9共10个稳态构成,每个稳态用10×10的矩阵表示。该矩阵直观地描述模拟阿拉伯数字,即将数字划分成10×10的矩阵,有数字的部分用1表示,空白部分用-1表示,如图9-2所示。网络对这10个稳态即10个数字(点阵)具有联想记忆的功能,当有带噪声的数字点阵输入到该网络时,网络的输出便可以得到最接近的目标向量(即10个稳态),从而达到正确识别的效果。

2.2 设计步骤

在此思路的基础上,设计Hopfield网络需要经过以下几个步骤,如图9-3所示。

1、输入输出设计——设计数字点阵(0～9)
如图9-2所示,有数字的部分用1表示,空白部分用-1表示,即可得到数字1和数字2的点阵:

array_one = 
[-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1
-1	-1	-1	-1	1	1	-1	-1	-1	-1];
array_two = 
[-1	1	1	1	1	1	1	1	1	-1
-1	1	1	1	1	1	1	1	1	-1
-1	-1	-1	-1	-1	-1	-1	1	1	-1
-1	-1	-1	-1	-1	-1	-1	1	1	-1
-1	1	1	1	1	1	1	1	1	-1
-1	1	1	1	1	1	1	1	1	-1
-1	1	1	-1	-1	-1	-1	-1	-1	-1
-1	1	1	-1	-1	-1	-1	-1	-1	-1
-1	1	1	1	1	1	1	1	1	-1
-1	1	1	1	1	1	1	1	1	-1];

其他的数字点阵以此类推。

        2．创建 Hopfield网络
        MATLAB神经网络工具箱为Hopfield网络提供了一些工具函数。10个数字点阵,即Hopfield网络的目标向量确定以后,可以借助这些函数,方便地创建Hopfield网络。具体过程见9.4节。
        3.产生带噪声的数字点阵
        带噪声的数字点阵,即点阵的某些位置的值发生了变化。模拟产生带噪声的数字矩阵方法有很多种,由于篇幅所限,本书仅列举两种比较常见的方法:固定噪声产生法和随机噪声产生法。
        4.数字识别测试
        将带噪声的数字点阵输入到创建好的Hopfield网络,网络的输出是与该数字点阵最为接近的目标向量,即0～9中的某个数字,从而实现联想记忆的功能。
        5.结果分析
        对测试的结果进行分析、比较,通过大量的测试来验证Hopfield 网络用于数字识别的可行性与有效性。

3 Hopfield网络的神经网络工具箱函数

MATLAB神经网络工具箱中包含了许多用于Hopfield网络分析与设计的函数,本节将详细说明常用的两个函数的功能、调用格式以及参数意义等。

3.1 Hopfield网络创建函数

newhop()函数用于创建一个离散型 Hopfield神经网络,其调用格式为:

net = newhop(T);

其中,T是具有Q个目标向量的RXQ矩阵(元素必须为-1或1);net为生成的神经网络,具有在T中的向量上稳定的点。
Hopfield神经网络仅有一层,其激活函数用satlins()函数。9.3.2 Hopfield网络仿真函数
sim()函数用于对神经网络进行仿真,其调用格式为:

[Y,Af,E, perf] = sim(net,P.Ai,T)
[Y,Af,E,perf] =sim(net,{Q TS} ,Ai,T)

其中,P,Q为测试向量的个数;Ai表示初始的层延时,默认为0;T表示测试向量(矩阵或元胞数组形式);TS为测试的步数;Y为网络的输出矢量;Af为训练终止时的层延迟状态;E为误差矢量; perf为网络的性能。

函数中用到的参数采取了两种不同的形式进行表示:矩阵和元胞数组。矩阵的形式只用于仿真的时间步长TS=1的场合,元胞数组形式常用于一些没有输入信号的神经网络。

4 MATLAB 实现

利用MATLAB神经网络工具箱提供的函数,将设计步骤一一在MATLAB环境下实现，matlab代码如下：

%% Hopfield神经网络的联想记忆——数字识别

%% 清空环境变量
clear all
clc

%% 数据导入
load data1 array_one
load data2 array_two

%% 训练样本（目标向量）
 T = [array_one;array_two]';
 
%% 创建网络
 net = newhop(T);
 
%% 数字1和2的带噪声数字点阵（固定法）
load data1_noisy noisy_array_one
load data2_noisy noisy_array_two

%% 数字1和2的带噪声数字点阵（随机法）

% noisy_array_one=array_one;
% noisy_array_two=array_two;
% for i = 1:100
%     a = rand;
%     if a < 0.3
%        noisy_array_one(i) = -array_one(i);
%        noisy_array_two(i) = -array_two(i);
%     end
% end

%% 数字识别

% 单步仿真——TS = 1(矩阵形式)
% identify_one = sim(net,10,[],noisy_array_one');  
% 多步仿真——元胞数组形式
noisy_one = {(noisy_array_one)'};                    
identify_one = sim(net,{10,10},{},noisy_one);
identify_one{10}';
noisy_two = {(noisy_array_two)'};
identify_two = sim(net,{10,10},{},noisy_two);
identify_two{10}';

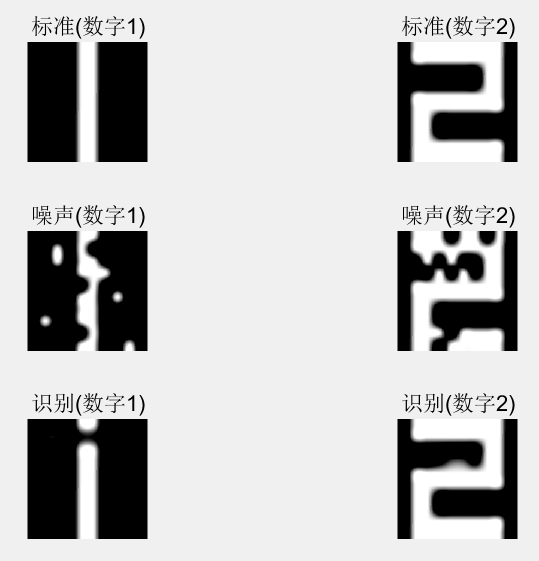
%% 结果显示
Array_one = imresize(array_one,20);
subplot(3,2,1)
imshow(Array_one)
title('标准(数字1)') 
Array_two = imresize(array_two,20);
subplot(3,2,2)
imshow(Array_two)
title('标准(数字2)') 
subplot(3,2,3)
Noisy_array_one = imresize(noisy_array_one,20);
imshow(Noisy_array_one)
title('噪声(数字1)') 
subplot(3,2,4)
Noisy_array_two = imresize(noisy_array_two,20);
imshow(Noisy_array_two)
title('噪声(数字2)')
subplot(3,2,5)
imshow(imresize(identify_one{10}',20))
title('识别(数字1)')
subplot(3,2,6)
imshow(imresize(identify_two{10}',20))
title('识别(数字2)')

5案例扩展

5.1识别效果讨论

图9-5所示是噪声强度为0.1(即10%的数字点阵位置值发生了改变)时的识别效果,从图中可以看出识别效果很好。进一步的研究发现,随着噪声强度的增加,识别效果逐渐下降。噪声强度为0.2和0.3时的识别结果分别如图9-6和图9-7所示,从图中不难看出,当噪声强度为0.3时,Hopfield已经很难对数字进行识别。

5.2应用扩展

离散型 Hopfield神经网络具有联想记忆的功能。近年来,越来越多的研究人员尝试着将Hopfield神经网络应用到各个领域,因此解决了很多传统方法难以解决的问题,如水质评价、发电机故障诊断、项目风险分析等。
将一些优化算法与离散Hopfield神经网络相结合,可以使其联想记忆能力更强,应用效果更为突出。例如,由于一般离散Hopfield神经网络存在很多伪稳定点,网络很难达到真正的稳态。将遗传算法应用到离散Hopfield神经网络中,利用遗传算法的全局搜索能力,对Hopfield联想记忆稳态进行优化,使待联想的模式跳出伪稳定点,从而使Hopfield网络在较高噪信比的情况下保持较高的联想成功率。