目录
- 数据结构:线索二叉树与线索化
- 线索二叉树的定义
- 线索化过程
- 线索化的应用
- 总结
- 5.3.2线索二叉树
- 1. 线索二叉树的概念与作用
- 2.线索二叉树的存储结构
- 3. 二叉树的线索化
- 1. 中序线索化
- 2. 先序线索化
- 3. 后序线索化
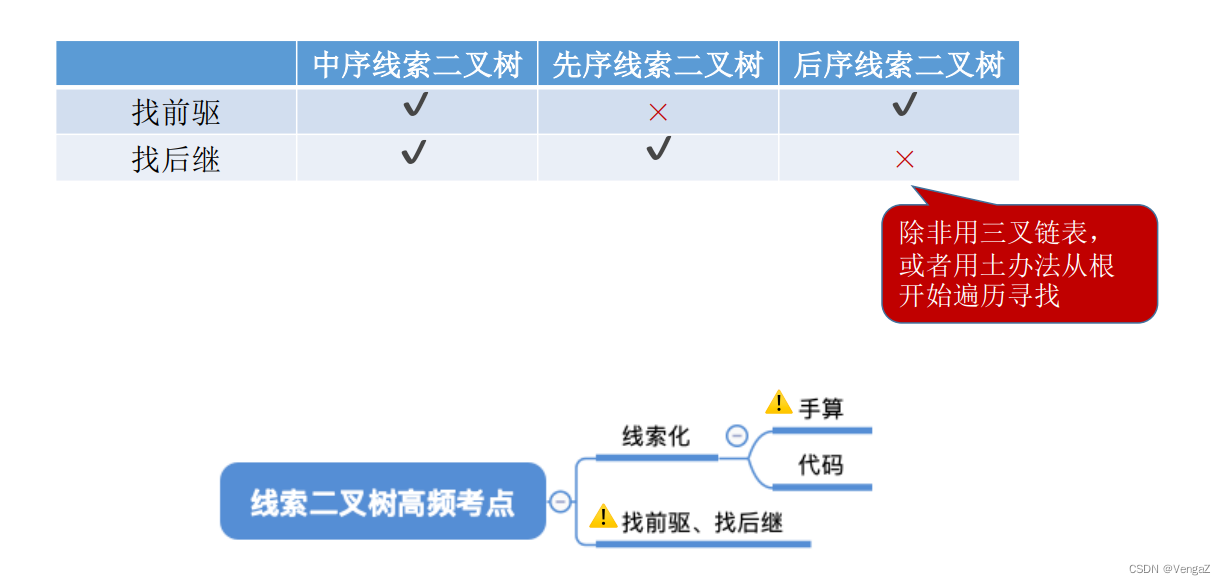
- 4. 线索树的寻找前驱后继的各种情况(多理解)
数据结构:线索二叉树与线索化
在二叉树中,每个节点最多有两个子节点,通常我们将其称为左子节点和右子节点。然而,在实际应用中,我们可能需要更高效地遍历二叉树,而传统的递归遍历方式可能会导致栈溢出或效率较低。线索二叉树是一种特殊的二叉树结构,通过添加线索化信息,使得我们可以在不使用递归或栈的情况下实现二叉树的遍历。
线索二叉树的定义
线索二叉树是对普通二叉树的扩展,它在每个节点中添加了两个指针,称为线索。这些线索指针将二叉树中的空指针转换为前驱或后继节点,从而形成了一种新的数据结构。
线索二叉树的特点:
- 线索化指针:每个节点的左子节点为空时,将其左指针线索化为其前驱节点;每个节点的右子节点为空时,将其右指针线索化为其后继节点。
- 前序线索化:节点的前序线索化是指将其左指针线索化为前驱节点,使得我们可以直接通过线索指针向前遍历。
- 中序线索化:节点的中序线索化是指将其右指针线索化为后继节点,使得我们可以直接通过线索指针向后遍历。
线索化过程
线索化二叉树的过程分为前序线索化、中序线索化和后序线索化三个步骤。以中序线索化为例进行说明:
- 对于节点p,若其左子节点为空,将左指针线索化为其前驱节点pre,并将标记bitLeftThread设置为1。
- 对于节点p的前驱节点pre,若其右子节点为空,将右指针线索化为其后继节点p,并将标记bitRightThread设置为1。
- 递归线索化节点p的左子树和右子树。
线索化的应用
线索二叉树的线索化过程使得二叉树的遍历更加高效,我们可以不需要使用递归或栈来实现遍历,而是通过线索化的指针直接进行前序、中序和后序的遍历。
线索化二叉树的应用场景包括:
- 高效的遍历算法:由于线索化的指针指向前驱和后继节点,我们可以在常数时间内找到下一个节点,从而提高遍历的效率。
- 空间优化:线索化二叉树不需要额外的栈空间来进行递归遍历,节省了存储空间。
总结
线索二叉树是一种特殊的二叉树结构,通过线索化的指针使得二叉树的遍历更加高效。线索化的过程可以将二叉树的空指针转换为前驱或后继节点,从而形成一种新的数据结构。线索二叉树的应用场景包括高效的遍历算法和空间优化。通过学习线索二叉树,我们可以更好地理解数据结构的应用和优化方法。
5.3.2线索二叉树
从某个节点的前驱后继、遍历都很不方便
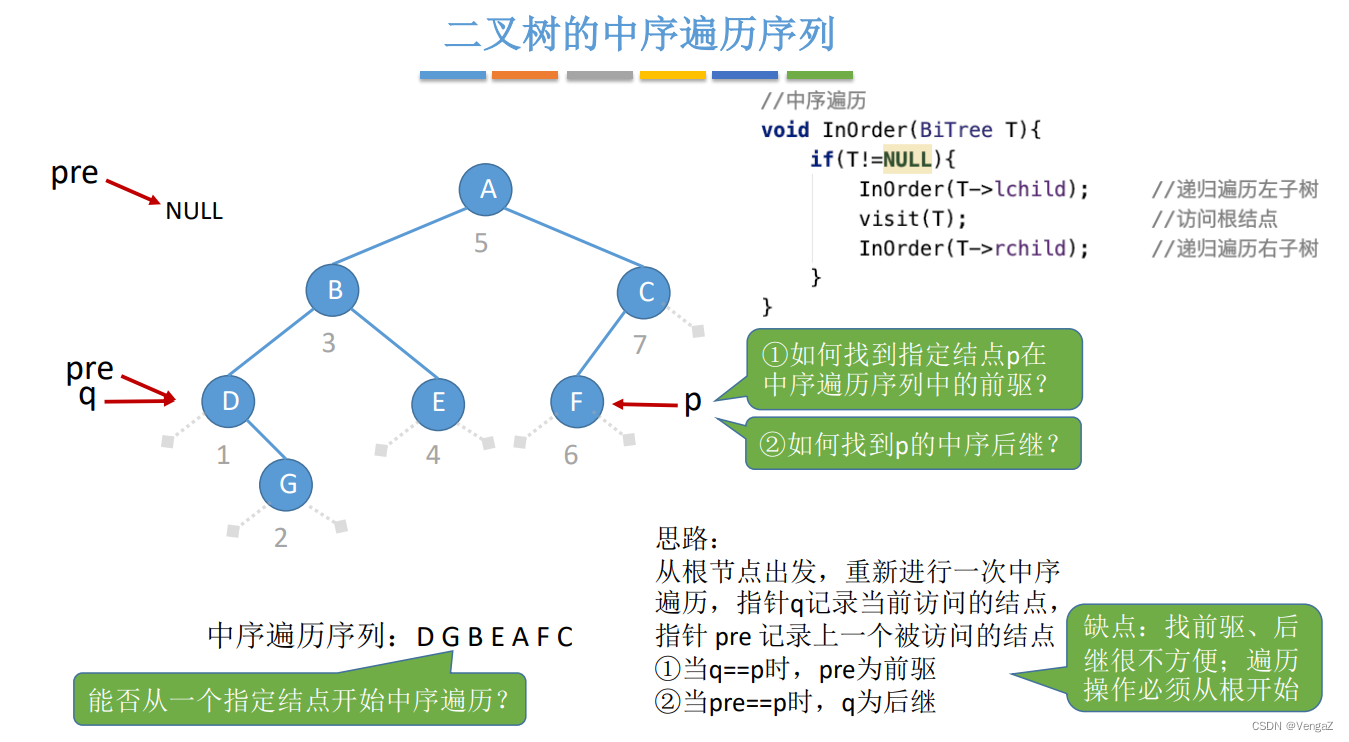
1. 线索二叉树的概念与作用
在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树以某种遍历方式(如先序、中序、后序或层次等)进行遍历,使其变为线索二叉树的过程称为对二叉树进行线索化。
2.线索二叉树的存储结构

- 中序线索二叉树——线索指向中序前驱、中序后继
//线索二叉树结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; // 左、右线索标志
}ThreadNode, *ThreadTree;
-
先序线索二叉树——线索指向先序前驱、先序后继
-
后序线索二叉树——线索指向后序前驱、后序后继
3. 二叉树的线索化

全局变量pre
1. 中序线索化
typedef struct ThreadNode{
int data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; // 左、右线索标志
}ThreadNode, *ThreadTree;
//全局变量pre, 指向当前访问的结点的前驱
TreadNode *pre=NULL;
void InThread(ThreadTree T){
if(T!=NULL){
InThread(T->lchild); //中序遍历左子树
visit(T); //访问根节点
InThread(T->rchild); //中序遍历右子树
}
}
void visit(ThreadNode *q){
if(q->lchid = NULL){ //左子树为空,建立前驱线索
q->lchild = pre;
q->ltag = 1;
}
if(pre!=NULL && pre->rchild = NULL){
pre->rchild = q; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = q;
}
//中序线索化二叉树T
void CreateInThread(ThreadTree T){
pre = NULL; //pre初始为NULL
if(T!=NULL);{ //非空二叉树才能进行线索化
InThread(T); //中序线索化二叉树
if(pre->rchild == NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}
2. 先序线索化
注意【转圈】问题,当ltag==0时,才能对左子树先序线索化
typedef struct ThreadNode{
int data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; // 左、右线索标志
}ThreadNode, *ThreadTree;
//全局变量pre, 指向当前访问的结点的前驱
TreadNode *pre=NULL;
//先序遍历二叉树,一边遍历一边线索化
void PreThread(ThreadTree T){
if(T!=NULL){
visit(T);
if(T->ltag == 0) //lchild不是前驱线索
//并且由于中序和后序都已经处理完了左子树,所以用不到lchild
PreThread(T->lchild);
PreThread(T->rchild);
}
}
void visit(ThreadNode *q){
if(q->lchid = NULL){ //左子树为空,建立前驱线索
q->lchild = pre;
q->ltag = 1;
}
if(pre!=NULL && pre->rchild = NULL){
pre->rchild = q; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = q;
}
//先序线索化二叉树T
void CreateInThread(ThreadTree T){
pre = NULL; //pre初始为NULL
if(T!=NULL);{ //非空二叉树才能进行线索化
PreThread(T); //先序线索化二叉树
if(pre->rchild == NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}
3. 后序线索化
typedef struct ThreadNode{
int data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; // 左、右线索标志
}ThreadNode, *ThreadTree;
//全局变量pre, 指向当前访问的结点的前驱
TreadNode *pre=NULL;
//先序遍历二叉树,一边遍历一边线索化
void PostThread(ThreadTree T){
if(T!=NULL){
PostThread(T->lchild);
PostThread(T->rchild);
visit(T); //访问根节点
}
}
void visit(ThreadNode *q){
if(q->lchid = NULL){ //左子树为空,建立前驱线索
q->lchild = pre;
q->ltag = 1;
}
if(pre!=NULL && pre->rchild = NULL){
pre->rchild = q; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = q;
}
//先序线索化二叉树T
void CreateInThread(ThreadTree T){
pre = NULL; //pre初始为NULL
if(T!=NULL);{ //非空二叉树才能进行线索化
PostThread(T); //后序线索化二叉树
if(pre->rchild == NULL)
pre->rtag=1; //处理遍历的最后一个结点
}
}
中序和后序都已经处理完了左子树,所以用不到lchild,也就不同考虑他的转圈问题
4. 线索树的寻找前驱后继的各种情况(多理解)