“Surely a Network That’s Big Enough Can Do Anything!”

“足够大的网络肯定能做任何事！”

The capabilities of something like ChatGPT seem so impressive that one might imagine that if one could just “keep going” and train larger and larger neural networks, then they’d eventually be able to “do everything”. And if one’s concerned with things that are readily accessible to immediate human thinking, it’s quite possible that this is the case. But the lesson of the past several hundred years of science is that there are things that can be figured out by formal processes, but aren’t readily accessible to immediate human thinking.

类似 ChatGPT 这样的能力看起来非常令人印象深刻，人们可能会想象，如果只是“继续下去”，训练越来越大的神经网络，它们最终就能够“做任何事”。如果关注的是那些容易被人类立即思考到的事物，那么这种说法很可能是正确的。但是从过去几百年的科学发展来看，有些东西可以通过正式的过程来解决，但却不能被人类的直观思维所轻易理解。

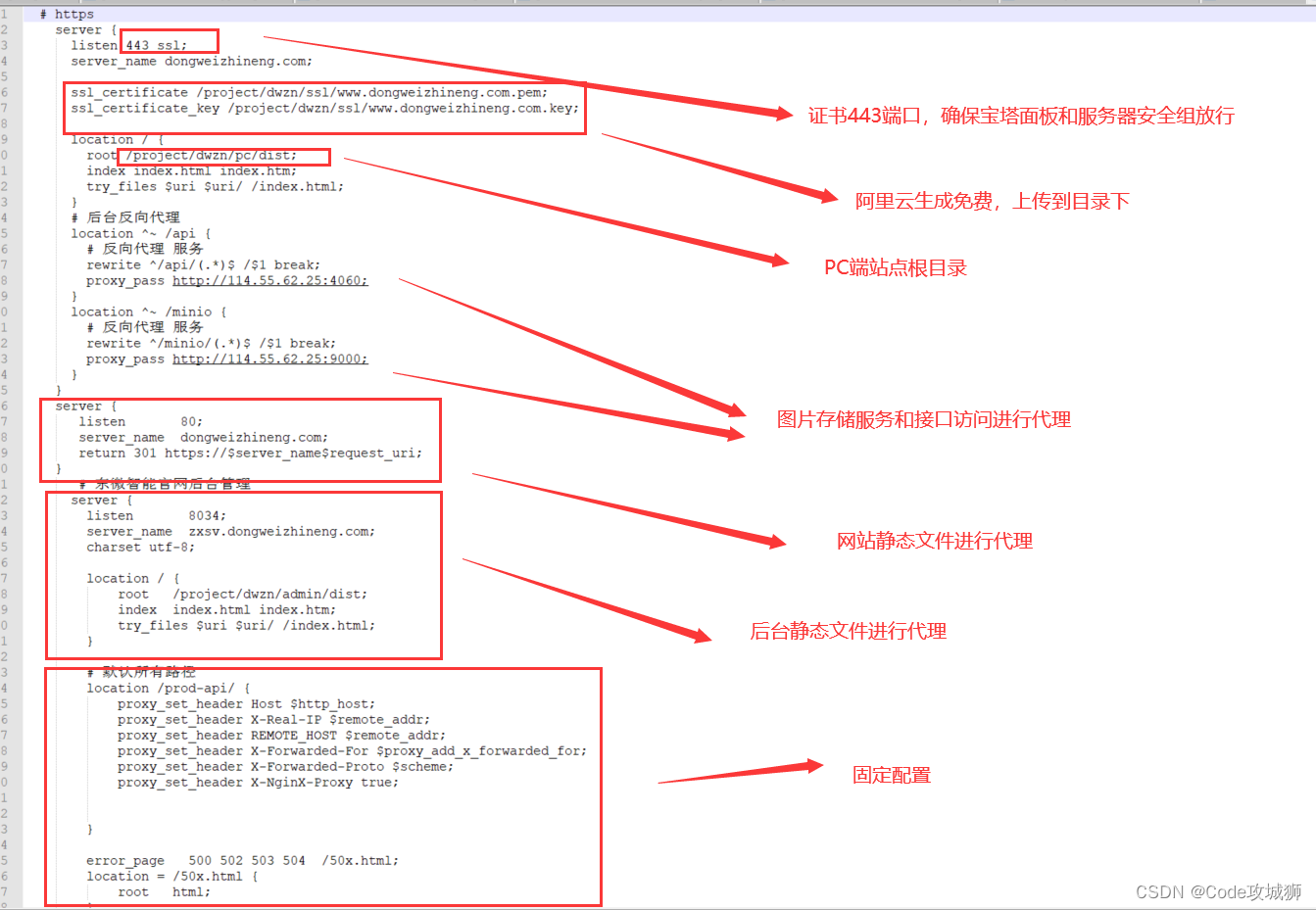
Nontrivial mathematics is one big example. But the general case is really computation. And ultimately the issue is the phenomenon of computational irreducibility. There are some computations which one might think would take many steps to do, but which can in fact be “reduced” to something quite immediate. But the discovery of computational irreducibility implies that this doesn’t always work. And instead there are processes—probably like the one below—where to work out what happens inevitably requires essentially tracing each computational step:

非平凡的数学就是一个很好的例子。但一般情况下，这实际上是关于计算的问题。归根结底，问题在于计算不可约性这个现象。有些计算看似需要很多步骤才能完成，但实际上可以“简化”为相当直接的东西。然而，计算不可约性的发现意味着这种方法并不总是奏效。相反，有些过程——可能就像下面这样的过程——要弄清楚会发生什么，实际上需要跟踪每一个计算步骤：

The kinds of things that we normally do with our brains are presumably specifically chosen to avoid computational irreducibility. It takes special effort to do math in one’s brain. And it’s in practice largely impossible to “think through” the steps in the operation of any nontrivial program just in one’s brain.

我们通常用大脑做的那些事情，大概是为了避免计算不可约性而特意挑选出来的。在大脑中进行数学运算需要付出特殊的努力。而在实践中，仅凭大脑“思考”任何非平凡程序的操作步骤基本上是不可能的。

But of course for that we have computers. And with computers we can readily do long, computationally irreducible things. And the key point is that there’s in general no shortcut for these.

但是，我们当然有计算机。有了计算机，我们就可以轻松地进行漫长的、计算不可约的事情。关键在于，通常情况下，这些事情是没有捷径的。

Yes, we could memorize lots of specific examples of what happens in some particular computational system. And maybe we could even see some (“computationally reducible”) patterns that would allow us to do a little generalization. But the point is that computational irreducibility means that we can never guarantee that the unexpected won’t happen—and it’s only by explicitly doing the computation that you can tell what actually happens in any particular case.

是的，我们可以记住许多特定计算系统中发生的具体事例。我们甚至可能看到一些（“计算可约的”）模式，这些模式允许我们进行一些概括。但关键是，计算不可约性意味着我们永远无法保证意想不到的事情不会发生——只有通过明确地进行计算，才能知道在任何特定情况下实际发生了什么。

And in the end there’s just a fundamental tension between learnability and computational irreducibility. Learning involves in effect compressing data by leveraging regularities. But computational irreducibility implies that ultimately there’s a limit to what regularities there may be.

归根结底，学习能力和计算不可约性之间存在一种根本的紧张关系。学习实际上是通过利用规律来压缩数据的过程。但计算不可约性意味着最终可能存在的规律是有限的。

As a practical matter, one can imagine building little computational devices—like cellular automata or Turing machines—into trainable systems like neural nets. And indeed such devices can serve as good “tools” for the neural net—like Wolfram|Alpha can be a good tool for ChatGPT. But computational irreducibility implies that one can’t expect to “get inside” those devices and have them learn.

就实际问题而言，可以想象将像元胞自动机或图灵机这样的小型计算设备构建到可训练的系统（如神经网络）中。实际上，这样的设备可以作为神经网络的良好“工具”——就像 Wolfram | Alpha 对 ChatGPT 来说是一个很好的工具。但计算不可约性意味着我们不能期望“深入了解”这些设备并让它们学会。

Or put another way, there’s an ultimate tradeoff between capability and trainability: the more you want a system to make “true use” of its computational capabilities, the more it’s going to show computational irreducibility, and the less it’s going to be trainable. And the more it’s fundamentally trainable, the less it’s going to be able to do sophisticated computation.

换句话说，能力和可训练性之间存在着最终的权衡：你希望一个系统更多地利用其计算能力，它就会表现出更多的计算不可约性，而且它的可训练性就会降低。一个系统的可训练性越高，它进行复杂计算的能力就越低。

(For ChatGPT as it currently is, the situation is actually much more extreme, because the neural net used to generate each token of output is a pure “feed-forward” network, without loops, and therefore has no ability to do any kind of computation with nontrivial “control flow”.)

（对于目前的 ChatGPT 来说，情况实际上要严重得多，因为用于生成每个输出标记的神经网络是纯粹的“前馈”网络，没有循环，因此无法进行任何具有非平凡“控制流”的计算。）

Of course, one might wonder whether it’s actually important to be able to do irreducible computations. And indeed for much of human history it wasn’t particularly important. But our modern technological world has been built on engineering that makes use of at least mathematical computations—and increasingly also more general computations. And if we look at the natural world, it’s full of irreducible computation—that we’re slowly understanding how to emulate and use for our technological purposes.

当然，人们可能会怀疑进行不可约计算是否真的重要。实际上，在人类历史的大部分时间里，这并不是特别重要。但是，我们现代的科技世界是建立在至少利用数学计算——以及越来越多的更普遍计算的基础上的。而且，如果我们观察自然界，它充满了不可约的计算——我们正在逐渐理解如何模仿和利用这些计算来实现我们的技术目的。

Yes, a neural net can certainly notice the kinds of regularities in the natural world that we might also readily notice with “unaided human thinking”. But if we want to work out things that are in the purview of mathematical or computational science the neural net isn’t going to be able to do it—unless it effectively “uses as a tool” an “ordinary” computational system.

是的，神经网络确实可以发现自然界中那些我们也可以通过“未经辅助的人类思考”轻易发现的规律。但是，如果我们想要研究数学或计算科学的领域内的事物，神经网络将无法做到这一点——除非它实际上将“普通”的计算系统作为工具“使用”。

But there’s something potentially confusing about all of this. In the past there were plenty of tasks—including writing essays—that we’ve assumed were somehow “fundamentally too hard” for computers. And now that we see them done by the likes of ChatGPT we tend to suddenly think that computers must have become vastly more powerful—in particular surpassing things they were already basically able to do (like progressively computing the behavior of computational systems like cellular automata).

但是关于这一切，有些东西可能令人困惑。在过去，有很多任务——包括写作文——我们认为对计算机来说“从根本上太难了”。而现在我们看到像 ChatGPT 这样的程序能够完成这些任务，我们往往会突然认为计算机一定变得非常强大——特别是在超过它们已经基本能够完成的事情（如逐步计算像元胞自动机这样的计算系统的行为）。

But this isn’t the right conclusion to draw. Computationally irreducible processes are still computationally irreducible, and are still fundamentally hard for computers—even if computers can readily compute their individual steps. And instead what we should conclude is that tasks—like writing essays—that we humans could do, but we didn’t think computers could do, are actually in some sense computationally easier than we thought.

然而，这并不是正确的结论。计算不可约的过程仍然是计算不可约的，并且对计算机来说仍然是根本性的难题——即使计算机可以轻松地计算它们的单个步骤。相反，我们应该得出的结论是，我们人类可以完成的任务——例如写作文——但我们认为计算机无法完成的任务，实际上在某种程度上比我们想象的要计算简单。

In other words, the reason a neural net can be successful in writing an essay is because writing an essay turns out to be a “computationally shallower” problem than we thought. And in a sense this takes us closer to “having a theory” of how we humans manage to do things like writing essays, or in general deal with language.

换句话说，神经网络能成功地写作文，是因为写作文的问题在计算上比我们想象的要“浅”。从某种意义上说，这使我们更接近“拥有一个理论”，来解释我们人类如何做到像写作文这样的事情，或者一般地处理语言。

If you had a big enough neural net then, yes, you might be able to do whatever humans can readily do. But you wouldn’t capture what the natural world in general can do—or that the tools that we’ve fashioned from the natural world can do. And it’s the use of those tools—both practical and conceptual—that have allowed us in recent centuries to transcend the boundaries of what’s accessible to “pure unaided human thought”, and capture for human purposes more of what’s out there in the physical and computational universe.

如果你有一个足够大的神经网络，那么，是的，你可能可以做到人类可以轻松完成的任何事情。但你无法捕捉到自然界普遍存在的能力，或者我们从自然界中创造出来的工具所具有的能力。正是这些工具——无论是实际的还是概念的——使我们在近几个世纪里能够超越“纯粹无助的人类思维”所能触及的界限，为人类目的捕捉到更多存在于物理和计算宇宙中的东西。

“点赞有美意，赞赏是鼓励”