题目描述

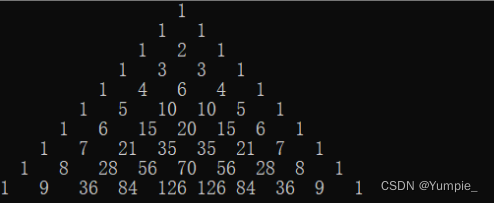
在屏幕上面打印杨辉三角。

算法思路

杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623----1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

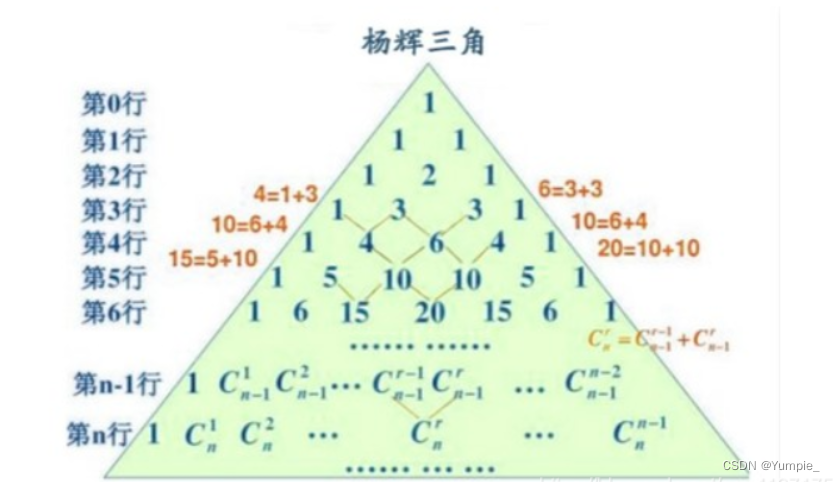
杨辉三角的特点：

1. 每个数等于它上方两数之和。

2. 每行数字左右对称，由1开始逐渐变大。

3. 第n行的数字有n项。

4. 前n行共[(1+n)n]/2 个数。

5. 第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

代码示例

基于以上杨辉三角所具有的特点，我们可以用代码进行实现。

精简版

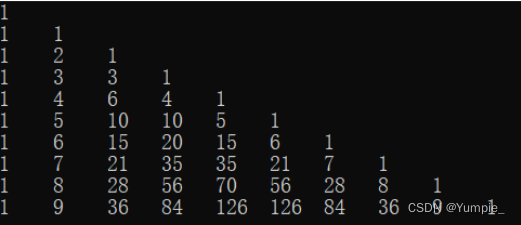
像上面的杨辉三角我们可以把它抽象一下，将前面的空格去掉：

我们可以看出上述图像中的特点：

1. 第一列和对角线都是1。
2. 其余元素等于上一行两个元素相加的和。

#include <stdio.h>
int main()
{
	int arr[10][10] = { 0 };
	int i = 0;
	int j = 0;
	for (i = 0; i < 10; i++)
	{
		for (j = 0; j <= i; j++)
		{
			if (j == 0)
				arr[i][j] = 1;
			if (i == j)
				arr[i][j] = 1;
			if(i>=2&&j>=1)
				arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
		}
		
	}
	for (i = 0; i < 10; i++)
	{
		for (j = 0; j <= i; j++)
		{
			printf("%-4d ", arr[i][j]);
		}
		printf("\n");
	}
	return 0;
}

优化版

我们发现在精简版的实现中，我们把杨辉三角有关数字打印出来了，但是我们没有打印出空格，我们发现在第一行数字、第二行…前面都有空格符，所以优化版主要解决空格问题。

#include <stdio.h>
#define N 10
 
int main()
{
	int arr[N][N] = { 0 };
	int i = 0;
	int j = 0;
	for (i = 0; i < N; i++)
	{
		int ret = (N - i - 1)*2;
		while (ret--)
		{
			printf(" ");
		}
		for (j = 0; j <= i; j++)
		{
			if (j == 0)
				arr[i][j] = 1;
			if (i == j)
				arr[i][j] = 1;
			if (i >= 2 && j >= 1)
				arr[i][j] = arr[i - 1][j] + arr[i - 1][j - 1];
			printf("%-3d ", arr[i][j]);
		
		}
		printf("\n");
 
	}
	
}