【算法提高：动态规划】1.6 区间DP

news2024/10/5 13:41:27

文章目录

  • 前言
  • 例题列表
    • 1068. 环形石子合并（前缀和 + 区间DP + 环形转换成线性⭐）
      • 如何把环转换成区间？⭐
      • 实现代码
      • 补充：相关题目——282. 石子合并
    • 320. 能量项链（另一种计算价值的石子合并）
    • 479. 加分二叉树🐂好题！⭐
      • 解法与代码
        • 如果求解最大值
        • 如果保留状态转移的过程
        • 代码
    • 1069. 凸多边形的划分（区间DP + 高精度计算）
      • 补充：相似题目——1039. 多边形三角剖分的最低得分
    • 321. 棋盘分割（二维前缀和 + 区间DP）🐂好题！
  • 相关链接

前言

根据笔者的经验，区间DP一般使用记忆化搜索会更好写一些。

例题列表

1068. 环形石子合并（前缀和 + 区间DP + 环形转换成线性⭐）

https://www.acwing.com/problem/content/1070/

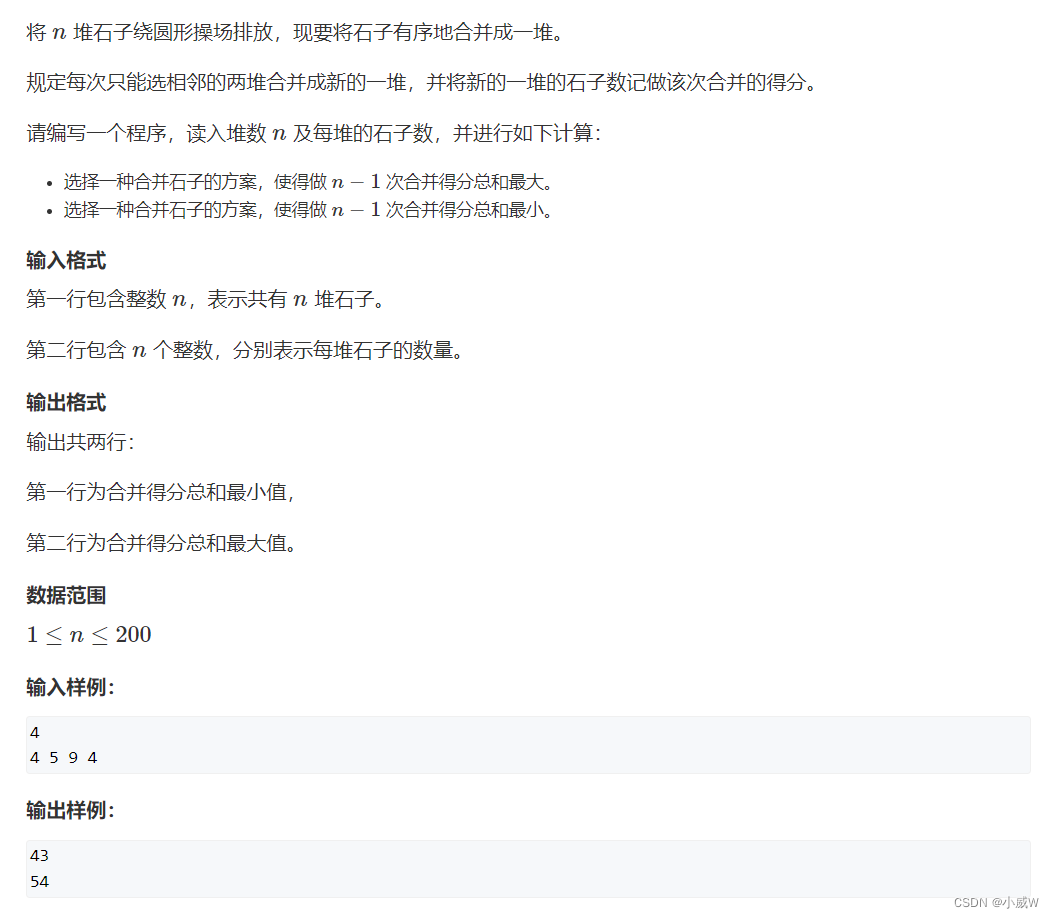
在这里插入图片描述

可以认为是 https://www.acwing.com/problem/content/284/ 的进阶版，从普通数组变成了环形数组。

如何把环转换成区间？⭐

在这里插入图片描述

将数组复制一份变成长度为 2 ∗ n 2*n 2∗n。
这样对这个 2 ∗ n 2*n 2∗n 求一下非环形数组的石子合并，最后枚举每个长度为 n 的区间的答案即可。

而不需要对每个长度为 n n n 的区间执行一次非环形数组的石子合并。

这样时间复杂度的差异就是 O ( n 3 ) O(n^3) O(n3) 和 O ( n 4 ) O(n^4) O(n4) 之间的差异。（因为普通数组类型的石子合并的时间复杂度是 O ( n 3 ) O(n^3) O(n3)）

实现代码

import java.io.BufferedInputStream;
import java.util.*;

public class Main {
    final static int N = 205;
    static int n;
    static int[] stones = new int[2 * N], sum = new int[2 * N];
    static int[][] mn = new int[2 * N][2 * N], mx = new int[2 * N][2 * N];
    static {
        for (int[] value : mn) Arrays.fill(value, Integer.MAX_VALUE);
        for (int[] ints : mx) Arrays.fill(ints, Integer.MIN_VALUE);
    }

    public static void main(String[] args) {
        Scanner sin = new Scanner(new BufferedInputStream(System.in));
        n = sin.nextInt();
        for (int i = 0; i < n; ++i) {
            stones[i] = stones[i + n] = sin.nextInt();
        }
        // 计算前缀和
        for (int i = 0; i < 2 * n; ++i) sum[i + 1] = sum[i] + stones[i];

        dfs(0, 2 * n - 1);
        int mnV = Integer.MAX_VALUE, mxV = Integer.MIN_VALUE;
        // 枚举所有长度为 n 的区间，更新答案
        for (int i = 0; i < n; ++i) {
            mnV = Math.min(mnV, mn[i][i + n - 1]);
            mxV = Math.max(mxV, mx[i][i + n - 1]);
        }
        System.out.println(mnV);
        System.out.println(mxV);
    }

    // 返回值是 {最小值，最大值}
    static int[] dfs(int l, int r) {
        if (l == r) return new int[]{0, 0};
        if (mn[l][r] != Integer.MAX_VALUE) return new int[]{mn[l][r], mx[l][r]};
        int mnV = Integer.MAX_VALUE, mxV = Integer.MIN_VALUE;
        for (int i = l; i < r; ++i) {
            // 拆成左右两部分计算，最后加上合并这整个区间的花费
            int[] res1 = dfs(l, i), res2 = dfs(i + 1, r);
            mnV = Math.min(mnV, sum[r + 1] - sum[l] + res1[0] + res2[0]);
            mxV = Math.max(mxV, sum[r + 1] - sum[l] + res1[1] + res2[1]);
        }
        mn[l][r] = mnV;
        mx[l][r] = mxV;
        return new int[]{mnV, mxV};
    }

}

补充：相关题目——282. 石子合并

282. 石子合并
见：【算法】区间DP （从记忆化搜索到递推DP）⭐

320. 能量项链（另一种计算价值的石子合并）

https://www.acwing.com/problem/content/322/

在这里插入图片描述

import java.io.BufferedInputStream;
import java.util.*;

public class Main {
    final static int N = 101 * 2;
    static int n;
    static int[][] memo = new int[N][N];    
    static int[] v = new int[N];            // 记录头标记

    public static void main(String[] args) {
        Scanner sin = new Scanner(new BufferedInputStream(System.in));
        n = sin.nextInt();
        for (int i = 0; i < n; ++i) {
            v[i] = v[i + n] = sin.nextInt();
        }
        dfs(0, 2 * n - 2);
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, memo[i][i + n - 1]);
        }
        System.out.println(ans);
    }
    
    static int dfs(int l, int r) {
        if (l == r) return 0;
        if (memo[l][r] != 0) return memo[l][r];
        int res = 0;
        for (int i = l; i < r; ++i) {
            res = Math.max(res, dfs(l, i) + dfs(i + 1, r) + v[l] * v[i + 1] * v[r + 1]);
        }
        return memo[l][r] = res;
    }
}

对于拆分成 (l, i) 和 (i + 1, r) ，三个相乘的值应该是 v[l]，v[i + 1]，v[r+1]。

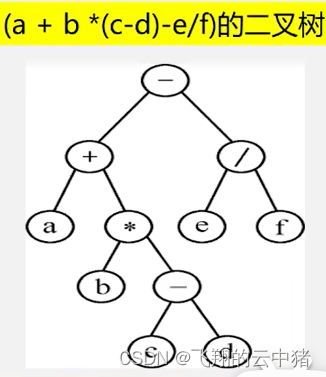
479. 加分二叉树🐂好题！⭐

https://www.acwing.com/activity/content/problem/content/1299/

在这里插入图片描述

这道题给出了中序遍历的二叉树，一个中序遍历并不能确定一个唯一的二叉树，因此我们要找到这些所有可能中，分值最大的那个二叉树。

根据题意，任一棵树的分值为：w[u] + tree(l) + tree®。

解法与代码

如果求解最大值

中序遍历中，每棵子树在中序遍历结果中都是连续的。
首先考虑 dp 数组的定义：dp[l][r] 表示所有中序遍历是 [l, r] 这一段的二叉树的集合，属性是 最大分值。

状态转移可以通过 枚举根节点是 [l, r] 中的哪一位来表示。

在这里插入图片描述

到这儿我们其实就知道如何求出最大值了，但是如何得到对应最大值时的前序遍历结果呢？（且题目要求输出字典序最小的方案——即根节点尽可能靠左）。

如果保留状态转移的过程

开设一个新数组 g[l][r] 存一下这个区间的根节点是哪个节点。

这样输出前序遍历结果时，就是先输出 g[1][n]，假设此时的根节点为 x，那么就递归地输出 g[1][x - 1] 和 g[x + 1][n]。

注意题目要求字典序最小的方案。

代码

dp 数组和 g 数组的定义见上文分析。

import java.io.BufferedInputStream;
import java.util.*;

public class Main {
    final static int N = 31;
    static int[][] dp = new int[N][N], g = new int[N][N];
    static int n;
    static int[] score = new int[N];

    public static void main(String[] args) {
        Scanner sin = new Scanner(new BufferedInputStream(System.in));
        n = sin.nextInt();
        for (int i = 1; i <= n; ++i) score[i] = sin.nextInt();
        System.out.println(dfs(1, n));
        dfs2(1, n);
    }

    static int dfs(int l, int r) {
        if (l > r) return 1;            // 子树为空，规定分数为1
        if (l == r) return score[l];    // 叶子的加分就是节点本身的分数
        if (dp[l][r] != 0) return dp[l][r];
        int res = 0;
        // 枚举 i 作为 l ~ r 之间的根节点
        for (int i = l; i <= r; ++i) {
            int v = dfs(l, i - 1) * dfs(i + 1, r) + score[i];
            if (v > res) {
                res = v;
                g[l][r] = i;
            }
        }
        return dp[l][r] = res;
    }
    
    // 前序遍历
    static void dfs2(int l, int r) {
        if (l == r) System.out.print(l + " ");
        else if (l < r) {
            int x = g[l][r];
            System.out.print(x + " ");
            dfs2(l, x - 1);
            dfs2(x + 1, r);
        }
    }
}

1069. 凸多边形的划分（区间DP + 高精度计算）

https://www.acwing.com/activity/content/problem/content/1300/

在这里插入图片描述

这道题的数值范围太大，需要使用大数计算或者字符模拟高精度计算。
这里我选择使用 Java 的 BigInteger 类型。
关于 Java 大数的相关链接可见：
Java【大数类】整理。
https://docs.oracle.com/en/java/javase/11/docs/api/java.base/java/math/BigInteger.html

import java.io.BufferedInputStream;
import java.math.BigInteger;
import java.util.*;

public class Main {
    final static int N = 51;
    static BigInteger[][] dp = new BigInteger[N][N];
    static int n;
    static BigInteger[] score = new BigInteger[N];
    static String s = "10000000000000000000000000000000";
    static BigInteger inf = new BigInteger(s);

    public static void main(String[] args) {
        Scanner sin = new Scanner(new BufferedInputStream(System.in));
        n = sin.nextInt();
        for (int i = 1; i <= n; ++i) score[i] = BigInteger.valueOf(sin.nextInt());
        for (int i = 0; i <= n; ++i) Arrays.fill(dp[i], new BigInteger(s));
        System.out.println(dfs(1, n));
    }

    static BigInteger dfs(int l, int r) {
        if (!dp[l][r].equals(inf)) return dp[l][r];
        if (l + 1 == r) return BigInteger.ZERO;
        for (int i = l + 1; i < r; ++i) {
            dp[l][r] = dp[l][r].min(dfs(l, i).add(dfs(i, r)).add(score[l].multiply(score[i]).multiply(score[r])));
        }
        return dp[l][r];
    }
}

补充：相似题目——1039. 多边形三角剖分的最低得分

1039. 多边形三角剖分的最低得分
题解见：【算法】区间DP （从记忆化搜索到递推DP）⭐

321. 棋盘分割（二维前缀和 + 区间DP）🐂好题！

https://www.acwing.com/activity/content/problem/content/1301/

在这里插入图片描述

这道题目看起来很吓人，但是很简单。

逐个分析，定义 dp 数组为 dp[x1][y1][x2][y2][k] 表示：将(x1,y1)(x2,y2)分成k部分的所有方案 的 均方差的平方的最小值。

为了求解均方差，我们可以求解均方差的平方，这样就在 dp 推导的过程中去掉了开根号的过程。

平均值 X 是可以提前计算的，就是整个棋盘的总分除以 n。

对于每一个小棋盘，它所贡献的均方差的平方就是 ( x i − x ) 2 / n (x_i - x)^2/n (xi​−x)2/n，其中 x i x_i xi​ 就是这个小棋盘的总分，这个总分可以通过二维前缀和来求。关于前缀和可见：【算法基础】1.5 前缀和与差分

整体代码如下：

import java.io.BufferedInputStream;
import java.math.BigInteger;
import java.util.*;

public class Main {
    final static int N = 15, M = 9;
    final static double INF = 1e9;
    static int n, m = 8;
    static int[][] sum = new int[M][M];     // 二维前缀和数组
    static double[][][][][] dp = new double[M][M][M][M][N];     // 将(x1,y1)(x2,y2)分成k部分的所有方案 的 均方差的平方的最小值
    static double x;


    public static void main(String[] args) {
        Scanner sin = new Scanner(new BufferedInputStream(System.in));
        n = sin.nextInt();      // 分成n个棋盘
        // 计算二维前缀和数组
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < m; ++j) {
                sum[i + 1][j + 1] = sin.nextInt() + sum[i + 1][j] + sum[i][j + 1] - sum[i][j];
            }
        }

        x = (double)sum[m][m] / n;
        System.out.printf("%.3f\n", Math.sqrt(dfs(1, 1, 8, 8, n)));
    }

    static double dfs(int x1, int y1, int x2, int y2, int k) {
        double v = dp[x1][y1][x2][y2][k];
        if (v != 0) return v;
        if (k == 1) return dp[x1][y1][x2][y2][k] = get(x1, y1, x2, y2);
        
        double res = INF;
        // 枚举横着切
        for (int i = x1; i < x2; ++i) {
            res = Math.min(res, get(x1, y1, i, y2) + dfs(i + 1, y1, x2, y2, k - 1));
            res = Math.min(res, get(i + 1, y1, x2, y2) + dfs(x1, y1, i, y2, k - 1));
        }
        
        // 枚举竖着切
        for (int i = y1; i < y2; ++i) {
            res = Math.min(res, get(x1, y1, x2, i) + dfs(x1, i + 1, x2, y2, k - 1));
            res = Math.min(res, get(x1, i + 1, x2, y2) + dfs(x1, y1, x2, i, k - 1));
        }
        return dp[x1][y1][x2][y2][k] = res;
    }

    // 得到这个棋盘的 (xi - x)^2 / n
    static double get(int x1, int y1, int x2, int y2) {
        double sum = getSum(x1, y1, x2, y2) - x;
        return sum * sum / n;
    }

    // 根据前缀和数组 得到一个矩形内的总分
    static int getSum(int x1, int y1, int x2, int y2) {
        return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
    }
}

相关链接

【算法】区间DP （从记忆化搜索到递推DP）⭐

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/828155.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

企业电子招标采购系统源码Spring Boot + Mybatis + Redis + Layui + 前后端分离 构建企业电子招采平台之立项流程图 tbms

企业电子招标采购系统源码Spring Boot + Mybatis + Redis + Layui + 前后端分离 构建企业电子招采平台之立项流程图 tbms

&#xfeff; 项目说明 随着公司的快速发展&#xff0c;企业人员和经营规模不断壮大&#xff0c;公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境&#xff0c;最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范&am…
阅读更多...
VBA技术资料MF38：VBA_在Excel中隐藏公式

VBA技术资料MF38：VBA_在Excel中隐藏公式

【分享成果&#xff0c;随喜正能量】佛祖也无能为力的四件事&#xff1a;第一&#xff0c;因果不可改&#xff0c;自因自果&#xff0c;别人是代替不了的&#xff1b;第二&#xff0c;智慧不可赐&#xff0c;任何人要开智慧&#xff0c;离不开自身的磨练&#xff1b;第三&#…
阅读更多...
Stable Diffusion - SDXL 1.0 全部样式设计与艺术家风格的配置与提示词

Stable Diffusion - SDXL 1.0 全部样式设计与艺术家风格的配置与提示词

欢迎关注我的CSDN&#xff1a;https://spike.blog.csdn.net/ 本文地址&#xff1a;https://spike.blog.csdn.net/article/details/132072482 来源于 Anna Dittmann 安娜迪特曼&#xff0c;艺术家风格的图像&#xff0c;融合幻想、数字艺术、纹理等样式。 SDXL 是 Stable Diffus…
阅读更多...
星戈瑞 | DSPE-PEG-CY3在生物医学研究中的作用

星戈瑞 | DSPE-PEG-CY3在生物医学研究中的作用

DSPE-PEG-CY3纳米颗粒在生物医学研究中具有多种重要作用&#xff0c;主要包括以下方面&#xff1a; 1. 荧光成像&#xff1a; DSPE-PEG-CY3纳米颗粒具有花菁染料CY3的荧光特性&#xff0c;可以被用作生物标记物&#xff0c;在细胞和生物体内进行荧光成像。这种荧光成像技术可以…
阅读更多...
基于fpga_EP4CE6F17C8_秒表计数器

基于fpga_EP4CE6F17C8_秒表计数器

文章目录 前言实验手册一、实验目的二、实验原理1&#xff0e;理论原理2&#xff0e;硬件原理 三、系统架构设计四、模块说明1&#xff0e;模块端口信号列表dig_driver(数码管驱动模块)key(按键消抖模块)top(顶层模块) 2&#xff0e;状态转移图3&#xff0e;时序图五、仿真波形…
阅读更多...
iOS数字转为图片

iOS数字转为图片

根据数字&#xff0c;转成对应的图片 - (void)viewDidLoad {[super viewDidLoad];[self testNum2String:10086]; }/// 根据数字&#xff0c;显示对应的图片 数字用特定的图片显示 - (void)testNum2String:(NSInteger)num {UIView *numContentView [[UIView alloc] initWithFr…
阅读更多...
多分支git合并流程

多分支git合并流程

阅读摘要 推荐一个git合并步骤,开发分支可能会多次提交合并到dev/master主干分支也会显示很多个提交点,这样不方便代码分支管理和回溯发布记录,所以推荐如下方法,不出意外,这也是个新手教程 git 合并步骤 本地开发分支建立格式建议 feature_功能_开始时间(示例 feature_test_…
阅读更多...
Java枚举解析：掌握枚举的绝佳指南！

Java枚举解析：掌握枚举的绝佳指南！

申明&#xff1a;本人于公众号Java筑基期&#xff0c;CSDN先后发当前文章&#xff0c;标明原创&#xff0c;转载二次发文请注明转载公众号&#xff0c;另外请不要再标原创 &#xff0c;注意违规 枚举 在Java中&#xff0c;枚举&#xff08;Enumeration&#xff09;是一种特殊的…
阅读更多...
MES管理系统解决方案，助力汽配行业打造数字化工厂

MES管理系统解决方案，助力汽配行业打造数字化工厂

汽配企业的生产与供应链体系必须与整车厂协同&#xff0c;才能确保品质和交期的要求。随着竞争的加剧&#xff0c;车企不断追求更精益化的管理&#xff0c;以应对市场挑战&#xff0c;而高端客户对品质、成本、交期也提出了更高的要求。因此&#xff0c;以合理的价格提供最佳质…
阅读更多...
Kubernetes架构和工作流程

Kubernetes架构和工作流程

目录 一、kubernetes简介 1.k8s的由来 2.为什么用 k8s &#xff1f; 3.k8s主要功能 二、k8s集群架构与组件 1.Master 组件 1.1Kube-apiserver 1.2Kube-controller-manager 1.3Kube-scheduler 2.Node组件 2.1Kubelet 2.2Kube-Proxy 2.3docker 或 rocket 3.配置存储中…
阅读更多...
C++中数据的输入输出介绍

C++中数据的输入输出介绍

C中数据的输入输出介绍 C中数据的输入输出涉及到的文件 <iostream>&#xff1a;这是C标准库中最常用的头文件之一&#xff0c;包含了进行标准输入输出操作的类和对象&#xff0c;如std::cin、std::cout、std::endl等。 <iomanip>&#xff1a;该头文件提供了一些用…
阅读更多...
算法与数据结构（五）--树【1】树与二叉树是什么

算法与数据结构（五）--树【1】树与二叉树是什么

一.树的定义 树是一个具有层次结构的集合&#xff0c;是由一个有限集和集合上定义的一种层次结构关系构成的。不同于线性表&#xff0c;树并不是线性的&#xff0c;而是有分支的。 树&#xff08;Tree&#xff09;是n&#xff08;n>0&#xff09;个结点的有限集。 若n0&…
阅读更多...
改变C++中私有变量成员的值

改变C++中私有变量成员的值

1、没有引用的情况&#xff1a; #include <iostream> #include <queue> using namespace std; class Person { public:queue<int>que; public:queue<int> getQueue(){return que;}void push(int a){que.push(a);}void pop(){que.pop();} };int main()…
阅读更多...
RS232自由转Profinet网关扫码枪连接电脑操作

RS232自由转Profinet网关扫码枪连接电脑操作

你是否曾经遇到过这样的问题&#xff1a;如何在不编写复杂代码的情况下&#xff0c;将条形码数据上传到PLC&#xff1f;今天&#xff0c;我们将为你揭示一个简单的解决方案&#xff01; 让我们来看看这个神奇的组合&#xff1a;捷米的JM-RS485/232-PN (rs232转Profient网关)和…
阅读更多...
背景图片及精灵图

背景图片及精灵图

.picture {width: 48px;height: 48px;background-image: url(../images/精灵图-侧边功能.png); }为一个有宽高的div设置了背景图片&#xff0c;背景图片只作用在div的content区域内&#xff0c;不作用在padding和border上。 知识点&#xff1a; 背景图使用精灵图&#xff08;…
阅读更多...
13-5_Qt 5.9 C++开发指南_基于信号量的线程同步_Semaphore

13-5_Qt 5.9 C++开发指南_基于信号量的线程同步_Semaphore

文章目录 1. 信号量的原理2. 双缓冲区数据采集和读取线程类设计3. QThreadDAQ和QThreadShow 的使用4. 源码4.1 可视化UI设计框架4.2 qmythread.h4.3 qmythread.cpp4.4 dialog.h4.5 dialog.cpp 1. 信号量的原理 信号量(Semaphore)是另一种限制对共享资源进行访问的线程同步机制…
阅读更多...
2023年8月美团外卖3-18元红包优惠券天天领取活动日历及美团外卖红包领取使用

2023年8月美团外卖3-18元红包优惠券天天领取活动日历及美团外卖红包领取使用

2023年8月美团外卖3-18元红包天天领取活动日历 根据上图美团外卖红包领取活动时间表以下时间可以天天领取3-18元美团外卖红包优惠券&#xff1a; 1、2023年8月18日 可领取美团外卖18元神券节红包&#xff1b; 2、2023年8月每周六、周日每天可领取12元美团外卖节红包&#xff…
阅读更多...
聊聊工程化 Docker 的最新趋势以及最佳实践

聊聊工程化 Docker 的最新趋势以及最佳实践

&#x1f337;&#x1f341; 博主猫头虎 带您 Go to New World.✨&#x1f341; &#x1f984; 博客首页——猫头虎的博客&#x1f390; &#x1f433;《面试题大全专栏》 文章图文并茂&#x1f995;生动形象&#x1f996;简单易学&#xff01;欢迎大家来踩踩~&#x1f33a; &a…
阅读更多...
AI绘画大师，轻松塑造绝美画作！

AI绘画大师，轻松塑造绝美画作！

前言 随着科技的不断进步&#xff0c;人工智能&#xff08;AI&#xff09;正逐渐渗透到各个领域&#xff0c;艺术也不例外。AI绘 画大师&#xff0c;即 AI 绘画 API&#xff0c;作为其中的一颗明珠&#xff0c;正在引领着艺术创作的革命&#xff0c;它为创作者和艺术爱好者带来…
阅读更多...
docker容器创建私有仓库（第三篇）

docker容器创建私有仓库（第三篇）

目录 六、创建私有仓库 七、Docker资源限制 7.1、CPU使用率 7.2、CPU共享比例 7.3、CPU周期限制 7.4、CPU核心限制 7.5、CPU 配额控制参数的混合案例 7.6、内存限制 7.7、Block IO 的限制 7.8、限制bps 和iops 8、Docker数据持久化 8.1、数据持久化介绍 8.2、Volum…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023