1.背景
重力恢复与气候实验(GRACE)观测地球重力势的时间变化。在考虑了大气和海洋效应后,每月到年际尺度上剩余的信号主要与陆地水储存(TWS)的变化有关。水储存变化的估计受到测量误差和噪声的信号退化影响,这些影响表现为随球谐谱阶数增加而增加的随机误差,以及在特定谱序内相关的系统误差。目前存在几种滤波方法,可以抑制或分离和去除这些误差。然而,在实际应用中,滤波器也会修改真实的地球物理信号。滤波器的设计专注于这种权衡,试图在最大程度减少信号损失的同时最大限度地减少噪声。
由于滤波后的GRACE数据的空间分辨率通常比其他水文数据集更粗,因此在进行公平的分析之前,有必要协调数据集之间的空间尺度差异。当未考虑由于对GRACE数据进行滤波而导致的信号修改时,地下水储存(TWS)估计之间的表观差异会错误地归因于观测或模型数据的缺陷,而实际上这些差异是由于空间尺度不匹配造成的。
调和空间分辨率差异的一种直接方法是以相同的方式对每个数据集进行滤波。这种方法先前已用于验证基于卫星的冬季降水估计 [Swenson, 2010] 和全球陆地水文模型 [例如,Schmidt et al., 2006]。另一种方法是对GRACE数据进行缩放,以考虑滤波对信号的影响。许多研究 [例如,Swenson and Wahr, 2007; Rodell et al., 2004a; Klees et al.,2007; Landerer et al., 2010] 已经估计了流域平均时间序列中的信号衰减,并对GRACE观测应用了增益因子。如果不进行恢复,信号衰减将减少关闭区域水平衡的能力,或者当将水量预算用于估计一个分量作为残差时,信号衰减将成为残差中的误差。由于GRACE数据用户通过所描述的途径估计信号退化非常繁琐,水文研究将极大受益于可以用作独立、独立和明确的水文应用数据集的网格化GRACE数据,无需测地学家的帮助 [Rodell et al., 2010]。这将使用户能够在用户定义的区域内对网格化GRACE数据进行平均,其中信号衰减已经作为GRACE后处理的一部分进行了校正,并且区域平均值的误差和不确定性也可以从网格化数据中计算出来。
2.滤波的方法
2.1 基本原理
我们通过未滤波和滤波后的月平均GLDAS-NOAH水储存估计之间的均方根差异(RMSD)来量化泄漏误差。为了减小这种泄漏误差,我们通过简单的最小二乘回归来推导出一个增益因子k,通过最小化未滤波、真实ΔSt和滤波后ΔSf储存时间序列之间的不匹配来实现:

这个方法采用最小二乘估计的方法,拟合参数k。下面我们以亚马逊流域的水储量变化在截断滤波前后的时间序列的散点为例。本质尺度因子就是要求得这个斜率k。

2.2 流域水储量的尺度因子估计
我们先获取流域水储量在截断滤波前后的时间序列,下面以亚马逊流域为例。

我们可以看到,由于截断滤波的关系,两者存在一定的差异。
下面我们进行尺度因子计算,代码如下:
%-------------------------------------------------------------------------%
% cs data from surface mass change %
% demo for grid scale factor
% Chistrong Wen@UCAS
%-------------------------------------------------------------------------%
tp_gind=load('amazon_new.txt');
GRID.lon=LLZ_CSR.lon;
GRID.lat=LLZ_CSR.lat;
amazon=inpolygon(interpn(GRID.lon,1),interpn(GRID.lat,1),tp_gind(:,1),tp_gind(:,2));
area_scale=cal_grid_region(GRID);
for ii=1:size(LLZ_CSR.rg,3)
CSR_rg_original(ii)=mean(mean(interpn(LLZ_CSR.rg(:,:,ii),1).*amazon.*interpn(area_scale,1)))/mean(mean(amazon.*interpn(area_scale,1)));
jgc_tt_original(ii)=LLZ_CSR.tt(ii);
end
%% filter time series
amazon=inpolygon(interpn(GRID.lon,1),interpn(GRID.lat,1),tp_gind(:,1),tp_gind(:,2));
area_scale=cal_grid_region(GRID);
for ii=1:size(Filter.rg,3)
CSR_rg_filter(ii)=mean(mean(interpn(Filter.rg(:,:,ii),1).*amazon.*interpn(area_scale,1)))/mean(mean(amazon.*interpn(area_scale,1)));
jgc_tt_filter(ii)=LLZ_CSR.tt(ii);
end
scatter(CSR_rg_original,CSR_rg_filter)
grid on
figure
plot(jgc_tt_original,CSR_rg_original)
hold on
plot(jgc_tt_filter,CSR_rg_filter,'g')
%% scale factor
[k] = polyfit(CSR_rg_filter,CSR_rg_original,1);
figure
subplot(2,1,1)
plot(jgc_tt_original,CSR_rg_original,'b','LineWidth',1)
hold on
plot(jgc_tt_filter,CSR_rg_filter,'k','LineWidth',1)
legend('GLDAS-NOAH:original','GLDAS-NOAH:filtered','best')
subplot(2,1,2)
plot(jgc_tt_original,CSR_rg_original,'b','LineWidth',1)
hold on
plot(jgc_tt_filter,CSR_rg_filter.*k(1),'r','LineWidth',1)
legend('GLDAS-NOAH:original','GLDAS-NOAH:filtered*scale factor','best')经过计算得到的尺度因子为1.0676.然后对滤波后的时间序列进行这个比例缩放,结果如图:

可以看到,经过尺度因子恢复之后的水储量与原始的结果很接近(下图)。
2.3 全球格网的尺度因子
如果我们对全球的水文模型每个分辨率格网进行尺度因子恢复,可以得到全球的尺度因子。本文使用的是GLDAS-NOAH 的SOIL MOISTURE为例,进行截断滤波,得到全球的尺度因子,同时我们读取GRACE JPL mascon发布的尺度因子进行对比:
代码:
%-------------------------------------------------------------------------%
% cs data from surface mass change %
% demo for grid scale factor %
%-------------------------------------------------------------------------%
% for ii=1:size(LLZ_CSR.lon,1)
% for jj=1:size(LLZ_CSR.lon,2)
% for kk=1:numel(LLZ_CSR.tt)
% GLDAS_original(kk)=LLZ_CSR.rg(ii,jj,kk);
% GLDAS_filter(kk)=Filter.rg(ii,jj,kk);
% end
% Temp = polyfit(GLDAS_filter,GLDAS_original,1);
% k(ii,jj) = Temp(1);
% end
% disp(ii)
% end
Scale.lon = LLZ_CSR.lon;
Scale.lat = LLZ_CSR.lat;
Scale.rg = k;
subplot(1,2,1)
rg_plot(Scale)
caxis([0,5]),colorbar
file = 'CLM4.SCALE_FACTOR.JPL.MSCNv03CRI.nc';
ncdisp(file)
lon = ncread(file,'lon');
lat = ncread(file,'lat');
[lon,lat] = meshgrid(lon,lat);
O.lon = lon;O.lat = lat;
O.rg = ncread(file,'scale_factor')';
subplot(1,2,2)
wzq_plot(O)
caxis([0,5]),colorbar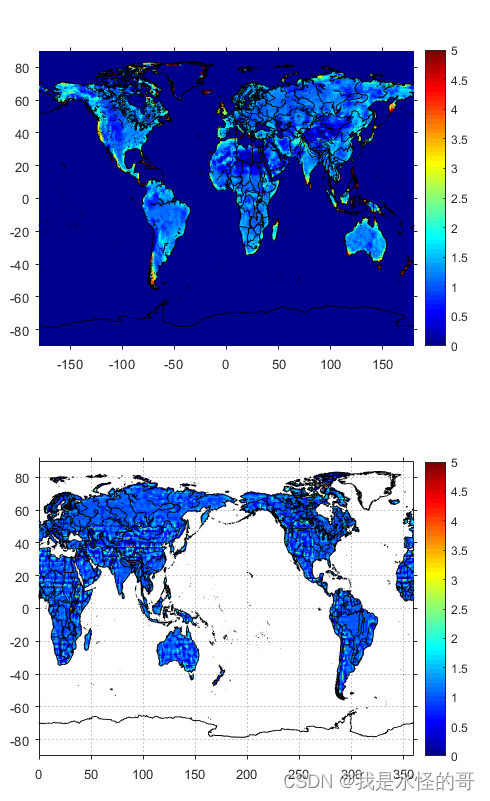
可以看到本文得到的尺度因子与JPL的量级一致,而JPL不包含海洋和格林兰岛。
代码中涉及的函数cal_grid_region
function sArea=cal_grid_region(OBS)
[Nlat,Nlon] = size(OBS.lat);
for nn=1:Nlat
llat(nn)=OBS.lat(nn,1);
end
DLat=abs(OBS.lat(1,1)-OBS.lat(2,1));
DLon=abs(OBS.lon(1,2)-OBS.lon(1,1));
% R_e=6.3781363000E+06; % m , the radius of EARTH
R_e = 6.371E+06;
for ii=1:numel(llat)
deg2rad = pi/180 ; %verlion
rLat0(ii)=(llat(ii)-DLat/2)*deg2rad;
rLat1(ii)=(llat(ii)+DLat/2)*deg2rad;
rArea(ii)= R_e^2*DLon*deg2rad*(cos(pi/2-rLat1(ii))-cos(pi/2-rLat0(ii)))*1D-6 ;
end
for ii=1:Nlat
for jj=1:Nlon
sArea(ii,jj)=rArea(ii); % km
end
end
end测试数据可以参见本文的资源。
参考资料
Landerer, F. W. and S. C. Swenson (2012). "Accuracy of scaled GRACE terrestrial water storage estimates." Water Resources Research 48(4).
GRACE mascon数据下载链接汇总_我是水怪的哥的博客-CSDN博客
绘图函数的使用wzq_plot - 哔哩哔哩 (bilibili.com)