文章目录
- 状态压缩DP
- 例题列表
- 棋盘式
- 1064. 小国王⭐🐂(好题!)
- 做题套路总结
- 327. 玉米田(好题!🐂 和1064. 小国王差不多的题目)
- 292. 炮兵阵地(和上面两道题差不多,需要多考虑上上一行)
- 集合
- 524. 愤怒的小鸟🚹🚹🚹(TODO)
- 529. 宝藏🚹🚹🚹🚹🚹(TODO)
- 相关链接
状态压缩DP
状压 DP 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。
更多介绍可见:相关链接 部分。
例题列表
棋盘式
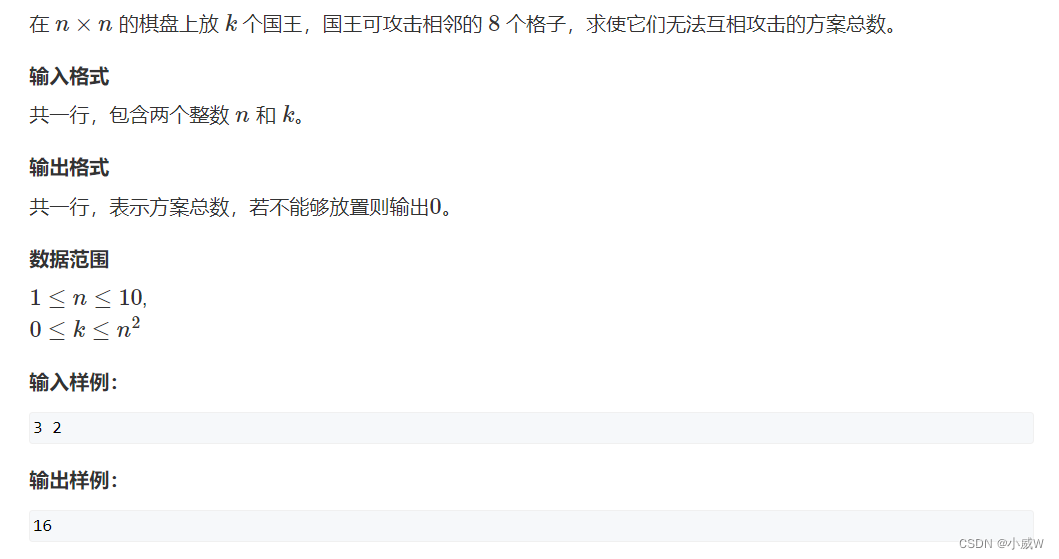
1064. 小国王⭐🐂(好题!)
https://www.acwing.com/activity/content/problem/content/1292/
洛谷相同题目链接:P1896 [SCOI2005] 互不侵犯
每个国王会攻击周围一圈儿。
每一层只需要考虑上一层的状态就可以了。
dp数组定义:long[][][] dp = new long[N][K][M]; 第i行,已经放了j个国王,当前行的国王集合为a,此时的方案数。
枚举顺序见代码。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
final static int N = 12, M = 1 << 10, K = 110; // 可以开大一点无所谓
static int n, m;
static List<Integer> state = new ArrayList<>(); // 里面存放的是在一行中没有冲突的集合
static int[] cnt = new int[M];
static List<Integer>[] head = new ArrayList[M]; // 里面存放的是每一种状态相邻的行可以放置哪些状态
static long[][][] dp = new long[N][K][M];
static {
Arrays.setAll(head, e -> new ArrayList<>());
}
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
n = sin.nextInt();
m = sin.nextInt();
// 预先处理出所有可选的状态集合(即在一行内没有冲突的集合),以及这种状态的行中有几个国王
for (int i = 0; i < 1 << n; ++i) {
if (check(i)) {
state.add(i);
cnt[i] = count(i);
}
}
// 预先处理每一行之后 相邻的行可以放置哪种状态集合
for (int i = 0; i < state.size(); ++i) {
for (int j = 0; j < state.size(); ++j) {
int a = state.get(i), b = state.get(j);
// 如果没有冲突
// 没有列上一样的,也没有列上相邻的
if ((a & b) == 0 && check(a | b)) {
head[i].add(j);
}
}
}
// 第i行,已经放了j个国王,当前行的国王集合为a
dp[0][0][0] = 1;
// 枚举每一行
for (int i = 1; i <= n + 1; i++) {
// 枚举已经选了m个国王(需要从0枚举到m)
for (int j = 0; j <= m; ++j) {
// 枚举每一种状态作为当前行(不管是不是合法的,无所谓,因为不合法的对应的head[a]里面是空的)
for (int a = 0; a < state.size(); ++a) {
// 枚举a后面可以跟着的每一种b
for (int b: head[a]) {
int c = cnt[state.get(a)];
// 如果当前已经选择的国王数量>=当前行的国王数量
if (j >= c) {
dp[i][j][a] += dp[i - 1][j - c][b];
}
}
}
}
}
System.out.println(dp[n + 1][m][0]);
}
// 检查一个状态集合是否在这一行内有冲突
static boolean check(int state) {
for (int i = 0; i < n; ++i) {
// 如果连续两列都为1,表示有冲突
if (((state >> i & 1) == 1 && (state >> i + 1 & 1) == 1)) return false;
}
return true;
}
// 计算这个状态集合中,摆放了几个国王
static int count(int state) {
int res = 0;
for (int i = 0; i < n; ++i) res += state >> i & 1;
return res;
}
}
做题套路总结
最后来总结一下写法:
- 先预先处理出,所有在一行中没有冲突的列集合
- 然后对计算出对所有合理列集合 来说 没有冲突的列集合
- 最后 枚举行、当前行的列状态、上一行的列状态,计算状态转移
327. 玉米田(好题!🐂 和1064. 小国王差不多的题目)
https://www.acwing.com/problem/content/329/
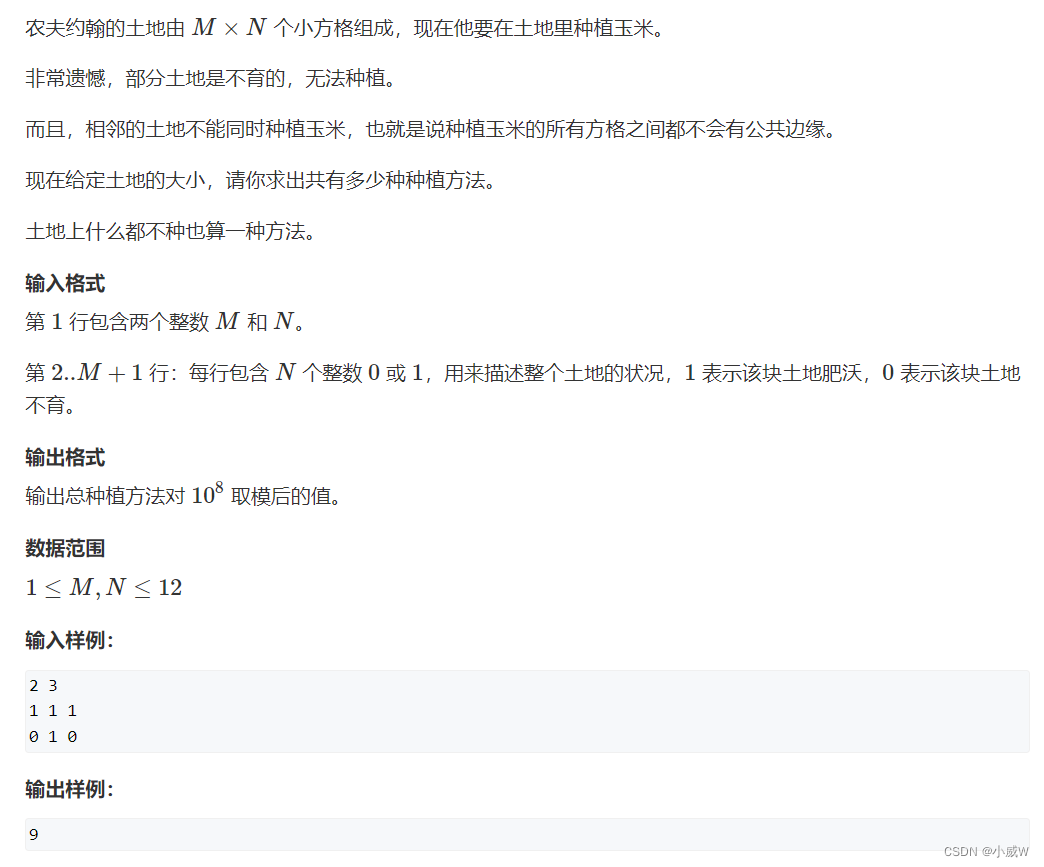
跟上一题相比有一些变化:
- 冲突的范围从周围一圈变成十字的形状
- 部分格子是无法放置玉米的
- 种植玉米的数量是没有限制的
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
final static int N = 14;
final static long MOD = (long)1e8;
static int m, n;
static int[] land = new int[N]; // 记录每一行中的哪些列是不能种植的
static List<Integer> states = new ArrayList<>(); // 记录所有在一行中合法的状态
static List<Integer>[] head = new ArrayList[1 << N];
static {
Arrays.setAll(head, e -> new ArrayList<>());
}
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
m = sin.nextInt();
n = sin.nextInt();
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < n; ++j) {
int t = sin.nextInt();
land[i] += (t ^ 1) << j; // 0表示不育
}
}
// 预先处理出在一行中合法的所有状态,加入states中
for (int i = 0; i < 1 << n; ++i) {
if (check(i)) states.add(i);
}
// 预先处理出哪两种行可以放在一起
for (int i = 0; i < states.size(); ++i) {
for (int j = 0; j < states.size(); ++j) {
int a = states.get(i), b = states.get(j);
// 只要这两行在列上没有重复,就可以放在一起
if ((a & b) == 0) {
head[i].add(j);
}
}
}
long[][] dp = new long[m + 2][states.size() + 1];
dp[0][0] = 1; // dp数组初始化
// 枚举每一行
for (int i = 1; i <= m + 1; ++i) {
// 枚举该行的状态
for (int j = 0; j < states.size(); ++j) {
if ((states.get(j) & land[i]) == 0) {
// 枚举可以从这种行转移过来的行
for (int k: head[j]) {
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % MOD;
}
}
}
}
System.out.println(dp[m + 1][0]);
}
static boolean check(int state) {
for (int i = 0; i < n - 1; ++i) {
// 检查是否有连续两位都是1的情况
if ((state >> i & 1) == 1 && ((state >> i + 1 & 1) == 1)) return false;
}
return true;
}
}
Q:为什么 dp[][] 数组初始化时只 设置 dp[0][0] = 1,而不把 所有 dp[0][j] = 1?
A:dp[0][0] = 1表示在还没有种植任何玉米的状态下(也就是前0行),这种情况只有1种。而dp[0][j] (j != 0)的含义是,在还没有种植任何玉米的状态下,最后一行(也就是不存在的这一行)的种植状态是states[j]的种植方式数量,这显然是不可能的,所以dp[0][j] (j != 0)都应该为0。
292. 炮兵阵地(和上面两道题差不多,需要多考虑上上一行)
https://www.acwing.com/problem/content/294/

跟上面两道题目相比,多考虑上上一行就好了。
dp 递推的过程也 多写一层循环。
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
final static int N = 105, M = 11;
static int n, m;
static int[] land = new int[N], cnt = new int[1 << M]; // 记录每一行,不能放置炮兵的列集合
static List<Integer> states = new ArrayList<>(); // 记录所有在一行中合理的列集合
static List<Integer>[] head = new ArrayList[1 << M];
static {
Arrays.setAll(head, e -> new ArrayList<>());
}
public static void main(String[] args) {
Scanner sin = new Scanner(new BufferedInputStream(System.in));
n = sin.nextInt();
m = sin.nextInt();
// 记录每一行不能被放置的列集合
for (int i = 1; i <= n; ++i) {
String s = sin.next();
for (int j = 0; j < m; ++j) {
land[i] += (s.charAt(j) == 'H'? 1: 0) << j;
}
}
// 计算出所有在一行中合理的列集合
for (int j = 0; j < 1 << m; ++j) {
if (check(j)) {
states.add(j);
cnt[j] = count(j);
}
}
// 计算出各个集合可以和哪些集合相邻
int l = states.size();
for (int i = 0; i < l; ++i) {
for (int j = 0; j < l; ++j) {
if ((states.get(i) & states.get(j)) == 0) {
head[i].add(j);
}
}
}
int[][][] dp = new int[n + 1][l][l];
// 枚举每一行
for (int r = 1; r <= n; ++r) {
// 枚举当前的每个集合
for (int i = 0; i < l; ++i) {
if ((states.get(i) & land[r]) == 0) {
// 枚举上一个集合
for (int j: head[i]) {
// 枚举上上个集合
for (int k: head[j]) {
if ((states.get(i) & states.get(k)) == 0) {
dp[r][j][i] = Math.max(dp[r - 1][k][j] + cnt[states.get(i)], dp[r][j][i]);
}
}
}
}
}
}
int ans = 0;
for (int i = 0; i < l; ++i) {
for (int j = 0; j < l; ++j) {
ans = Math.max(ans, dp[n][i][j]);
}
}
System.out.println(ans);
}
private static boolean check(int state) {
for (int i = 0; i < m; ++i) { // 这里最好写成 i < m,写成 i < m - 2 时答案就不对了
// 邻近两个范围内不能有炮兵
if ((state >> i & 1) == 1 && ((state >> i + 1 & 1) == 1 || (state >> i + 2 & 1) == 1)) return false;
}
return true;
}
// 计算这种集合中有多少个炮兵
static int count(int state) {
int res = 0;
for (int i = 0; i < m; ++i) res += state >> i & 1;
return res;
}
}
集合
524. 愤怒的小鸟🚹🚹🚹(TODO)
https://www.acwing.com/problem/content/526/


数据范围:
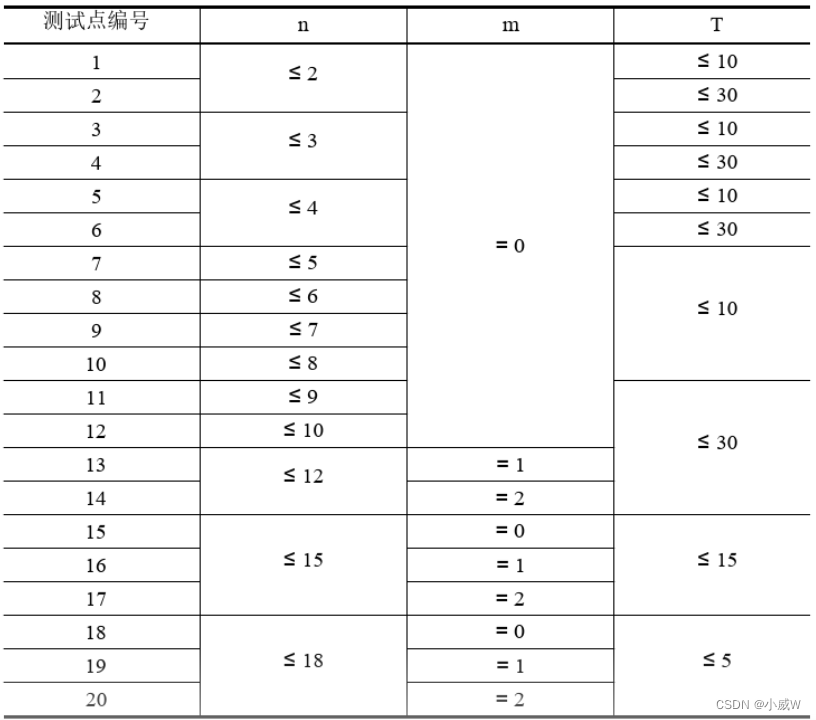
在这里插入代码片
529. 宝藏🚹🚹🚹🚹🚹(TODO)
https://www.acwing.com/problem/content/531/

在这里插入代码片
相关链接
从集合论到位运算——常见位运算技巧及相关习题 & 状态压缩DP
【力扣周赛】第 355 场周赛(构造&二分答案&异或前缀 状态压缩⭐)
【算法基础:动态规划】5.4 状态压缩DP