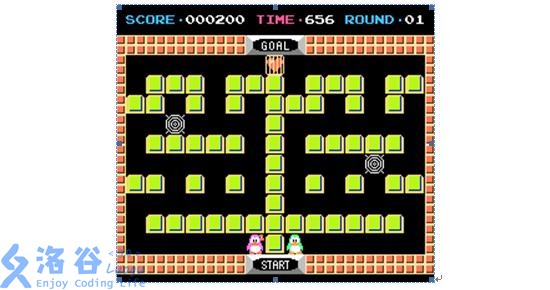
[TJOI2008] Binary Land

题目背景

Binary Land是一款任天堂红白机上的经典游戏，讲述的是两只相爱的企鹅Gurin和Malon的故事。两只企鹅在一个封闭的迷宫中，你可以控制他们向上下左右四个方向移动。但是他们的移动有一个奇怪的规则，即如果你按“上”或“下”方向键，两只企鹅会同时向上移动或向下移动1格；如果你按“左”方向键，则Malon向左移动1格，同时Gurin向右移动1格；如果你按“右”方向键，则Malon向右移动1格，Gurin向左移动1格。当然，如果某只企鹅被障碍挡住，它就不会移动了。另外，在迷宫的某些格子处有蜘蛛网，如果任何一只企鹅进入这种格子，则游戏失败。两只企鹅不会相互阻挡，即在相向运动时他们可以“穿过”彼此，也可以同时处于同一格子里。迷宫的某个格子上有一颗红心，游戏的任务就是使两只企鹅同时到达这个格子。

题目描述

请编写程序找出完成任务所需的最少的操作步数。如果无法完成目标，输出“no”。

输入格式

第一行包含两个整数R, C 表示迷宫的长和宽。

按下来有R行，每行包含C个字符，描述了一个迷宫。其中’#’表示企鹅不能通过的障碍物，’X’表示蜘蛛网，’.’表示空地，’G’表示Gurin的初始位置，’M’表示Malon的初始位置，’T’表示终点位置。

输入数据保证标有’G’,’M’,’T’的格子分别只有一个，保证企鹅不可能走到迷宫以外。

输出格式

输出只有一行，为最少的操作步数。如果不能完成任务，输出“no”。

样例 #1

样例输入 #1

4 7
#######
#..T..#
#G##M##
#######

样例输出 #1

提示

满足要求的一个操作序列为：上－右－左－左

3 ≤ R, C ≤ 30

分析

使用bfs即可，开结构体需记录两只企鹅的坐标，当然还有操作步数

代码

#include <bits/stdc++.h>
using namespace std;
const int M = 35;
int  r, c;
bool st[M][M][M][M];
char g[M][M];
struct point {
    int x1, y1;
    int x2, y2;
    int u;
    point(int x1=0, int y1=0, int x2=0, int y2=0,int u=0) :x1(x1), y1(y1), x2(x2), y2(y2),u(u) {}
};
queue<point> q;
int lsx, lsy;
point read() {
    point fi;
    cin >> r >> c;
    memset(st, false, sizeof(st));
    for (int i = 1; i <= r; i++)
        for (int j = 1; j <= c; j++) {
            char& tmp = g[i][j];
            cin >> tmp;
            if (tmp == 'G') fi.x1 = i, fi.y1 = j;
            if (tmp == 'M') fi.x2 = i, fi.y2 = j;
            if (tmp == 'T') lsx = i, lsy = j;
        }
    st[fi.x1][fi.y1][fi.x2][fi.y2] = 1;
    fi.u = 0;
    return fi;
}
int check(point t) {
    if (g[t.x1][t.y1] == 'X' or g[t.x2][t.y2] == 'X') return -1;
    if (g[t.x1][t.y1] == '#' and g[t.x2][t.y2] == '#') return -1;
    if (g[t.x1][t.y1] == '#') return 1;
    if (g[t.x2][t.y2] == '#') return 2;
    return 0;
}
void update1(point t, int i) {
    point u(t);
    u.x1 += i; u.x2 += i; bool f = 1; u.u++;
    switch (check(u))
    {
    case 1: {u.x1-=i; break; }
    case 2: {u.x2-=i; break; }
    case 0: {break; }
    default: {f = 0; break; } 
    }
    if (f and !st[u.x1][u.y1][u.x2][u.y2]) q.push(u), st[u.x1][u.y1][u.x2][u.y2] =  1;
}
void updw(point t) {
    update1(t, 1);
    update1(t, -1);
}
void update2(point t, int i,int j) {
    point u(t);
    u.y1 += i; u.y2 += j; bool f = 1; u.u++;
    switch (check(u))
    {
    case 1: {u.y1 -= i; break; }
    case 2: {u.y2 -= j; break; }
    case 0: {break; }
    default: {f = 0; break; }
    }
    if (f and !st[u.x1][u.y1][u.x2][u.y2]) q.push(u), st[u.x1][u.y1][u.x2][u.y2] = 1;
}
void lfrg(point t) {
    update2(t, 1, -1);
    update2(t, -1, 1);
}
int bfs() {
    q.push(read());
    while (!q.empty()) {
        point now = q.front(); q.pop();
        if (now.x1 == lsx and now.x2 == lsx and now.y1 == lsy and now.y2 == lsy) return now.u;
        updw(now);
        lfrg(now);
    }
    return -1;
}

int main() {
    int ans = bfs();
    if (ans == -1) cout << "no";
    else cout << ans;
    return 0;
}

代码分析

代码较长，分多部分看
1.bfs

int bfs() {
    q.push(read());
    while (!q.empty()) {
        point now = q.front(); q.pop();
        if (now.x1 == lsx and now.x2 == lsx and now.y1 == lsy and now.y2 == lsy) return now.u;
        updw(now);
        lfrg(now);
    }
    return -1;
}

基本的bfs，取队头后再入队其他的值，其中updw(now); lfrg(now);函数的作用分别为尝试上下移动，尝试左右移动
2.updw/lfrg
这两个函数每个都代表了两种操作
由于基本相同，我们只看上下移动的：

void update1(point t, int i) {
    point u(t);
    u.x1 += i; u.x2 += i; bool f = 1; u.u++;
    switch (check(u))
    {
    case 1: {u.x1-=i; break; }
    case 2: {u.x2-=i; break; }
    case 0: {break; }
    default: {f = 0; break; } 
    }
    if (f and !st[u.x1][u.y1][u.x2][u.y2]) q.push(u), st[u.x1][u.y1][u.x2][u.y2] =  1;
}

这是updw函数中调用的函数
首先，我们使状态t进行上下移动，更新步数，后调用check，判断是否合法，此时分4种情况

int check(point t) {
    if (g[t.x1][t.y1] == 'X' or g[t.x2][t.y2] == 'X') return -1;
    if (g[t.x1][t.y1] == '#' and g[t.x2][t.y2] == '#') return -1;
    if (g[t.x1][t.y1] == '#') return 1;
    if (g[t.x2][t.y2] == '#') return 2;
    return 0;
}