k-medoids聚类简介

k-medoids是另一种聚类算法，可用于在数据集中查找分组。k-medoids聚类与k-means聚类非常相似，除了一些区别。k-medoids聚类算法的优化功能与k-means略有不同。最近我们被客户要求撰写关于聚类的研究报告，包括一些图形和统计输出。在本节中，我们将研究k-medoids聚类。

 

 【视频】KMEANS均值聚类和层次聚类：R语言分析生活幸福质量系数可视化实例

，时长06:05

---

k-medoids聚类算法

有许多不同类型的算法可以执行k-medoids聚类，其中最简单，最有效的算法是PAM。在PAM中，我们执行以下步骤来查找集群中心：

1. 从散点图中选择k个数据点作为聚类中心的起点。

2. 计算它们与散点图中所有点的距离。

3. 将每个点分类到最接近中心的聚类中。

4. 在每个群集中选择一个新点，以使该群集中所有点与自身的距离之和最小。

5. 重复  步骤2，  直到中心停止变化。

可以看到，除了步骤1  和  步骤4之外，PAM算法与k-means聚类算法相同  。对于大多数实际目的，k-medoids聚类给出的结果几乎与k-means聚类相同。但是在某些特殊情况下，我们在数据集中有离群值，因此首选k-medoids聚类，因为它比离群值更健壮。

k-medoids聚类代码

在本节中，我们将使用在上两节中使用的相同的鸢尾花数据集，并进行比较以查看结果是否明显不同于上次获得的结果。

实现k-medoid聚类

在本练习中，我们将使用R的预构建库执行k-medoids：

1. 将数据集的前两列存储在  iris_data  变量中：

   iris_data<-iris[,1:2]

2. 安装  软件包：

   install.packages("cluster")

3. 导入  软件包：

   library("cluster")

4. 将PAM聚类结果存储在  km.res  变量中：

   km<-pam(iris_data,3)

5. 导入库：

   library("factoextra")

6. 在图中绘制PAM聚类结果：

   fviz_cluster(km, data = iris_data,palette = "jco",ggtheme = theme_minimal())

   输出如下：

   图：k-medoids聚类的结果

k-medoids聚类的结果与我们在上一节中所做的k-means聚类的结果没有太大差异。

因此，我们可以看到前面的PAM算法将我们的数据集分为三个聚类，这三个聚类与我们通过k均值聚类得到的聚类相似。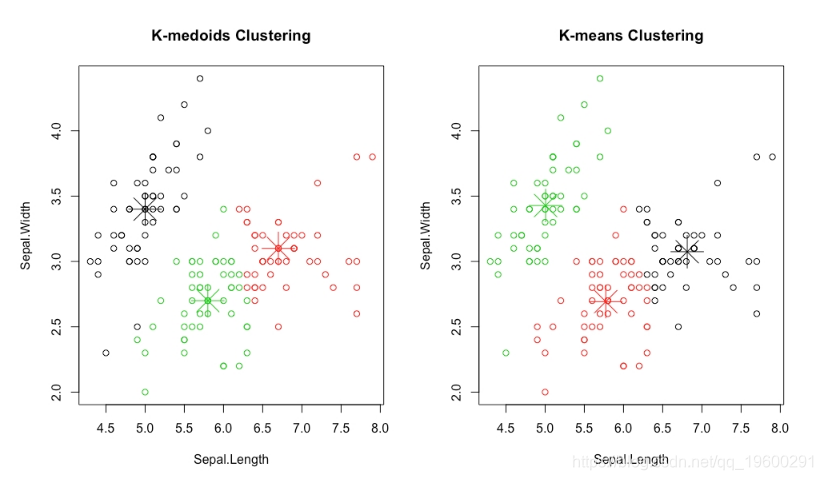

图：k-medoids聚类与k-means聚类的结果

在前面的图中，观察k均值聚类和k均值聚类的中心如何如此接近，但是k均值聚类的中心直接重叠在数据中已有的点上，而k均值聚类的中心不是。

k-均值聚类与k-medoids聚类

现在我们已经研究了k-means和k-medoids聚类，它们几乎是完全相同的，我们将研究它们之间的区别以及何时使用哪种类型的聚类：

• 计算复杂度：在这两种方法中，k-medoids聚类在计算上更加复杂。当我们的数据集太大（> 10,000点）并且我们想要节省计算时间时，相对于k-medoids聚类，我们更倾向于k-means聚类。

  数据集是否很大完全取决于可用的计算能力。

• 离群值的存在：k均值聚类比离群值更容易对离群值敏感。

• 聚类中心：k均值算法和k聚类算法都以不同的方式找到聚类中心。

使用k-medoids聚类进行客户细分

使用客户数据集执行k-means和k-medoids聚类，然后比较结果。

步骤：

1. 仅选择两列，即杂货店和冷冻店，以方便地对集群进行二维可视化。

2. 使用k-medoids聚类绘制一个图表，显示该数据的四个聚类。

3. 使用k均值聚类绘制四簇图。

4. 比较两个图，以评论两种方法的结果如何不同。

结果将是群集的k均值图，如下所示：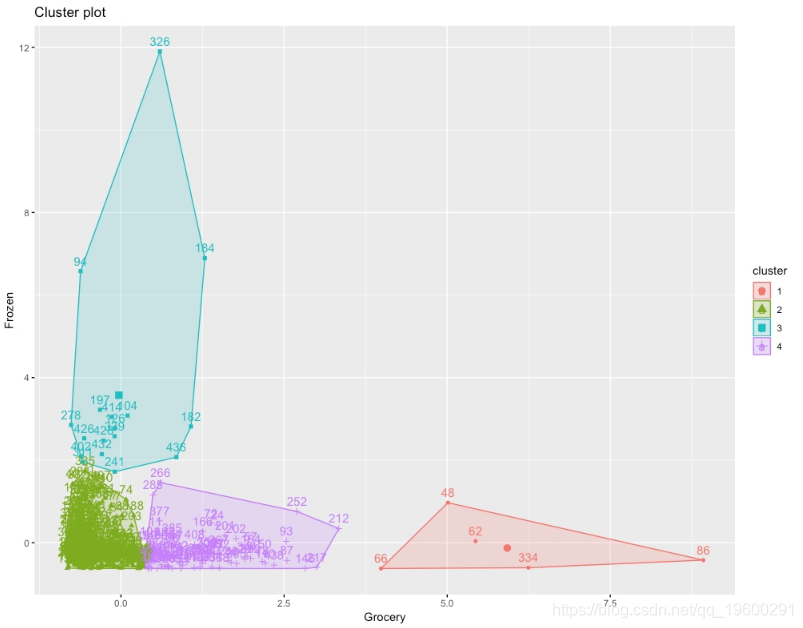

图：集群的预期k均值图

确定最佳群集数

到目前为止，我们一直在研究鸢尾花数据集，在该数据集中我们知道有多少种花，并根据这一知识选择将数据集分为三个簇。但是，在无监督学习中，我们的主要任务是处理没有任何信息的数据，例如，数据集中有多少个自然簇或类别。同样，聚类也可以是探索性数据分析的一种形式。

聚类指标的类型

确定无监督学习中最佳聚类数的方法不止一种。以下是我们将在本章中研究的内容：

• 轮廓分数

• 弯头法/ WSS

• 差距统计

轮廓分数

轮廓分数或平均轮廓分数计算用于量化通过聚类算法实现的聚类质量。

轮廓分数在1到-1之间。如果聚类的轮廓分数较低（介于0和-1之间），则表示该聚类散布开或该聚类的点之间的距离较高。如果聚类的轮廓分数很高（接近1），则表示聚类定义良好，并且聚类的点之间的距离较低，而与其他聚类的点之间的距离较高。因此，理想的轮廓分数接近1。

计算轮廓分数

我们学习如何计算具有固定数量簇的数据集的轮廓分数：

1. 将iris数据集的前两列（隔片长度和隔片宽度）放在  iris_data  变量中：

2. 执行k-means集群：

3. 将k均值集群存储在  km.res  变量中：

4. 将所有数据点的成对距离矩阵存储在  pair_dis  变量中：

5. 计算数据集中每个点的轮廓分数：

6. 绘制轮廓分数图：

   输出如下：

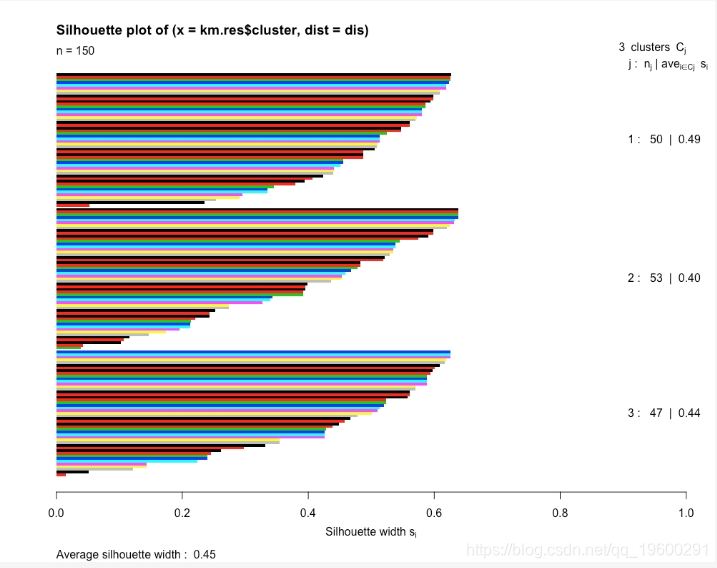
7. 图：每个群集中每个点的轮廓分数用单个条形表示

前面的图给出了数据集的平均轮廓分数为0.45。它还显示了聚类和点聚类的平均轮廓分数。

我们计算了三个聚类的轮廓分数。但是，要确定要拥有多少个群集，就必须计算数据集中多个群集的轮廓分数。

确定最佳群集数

针对k的各个值计算轮廓分数来确定最佳的簇数：

从前面的图中，选择得分最高的k值；即2。根据轮廓分数，聚类的最佳数量为2。

1. 将数据集的前两列（长度和宽度）放在  iris_data  变量中：

2. 导入  库

3. 绘制轮廓分数与簇数（最多20个）的图形：

   注意

   在第二个参数中，可以将k-means更改为k-medoids或任何其他类型的聚类。

   输出如下：

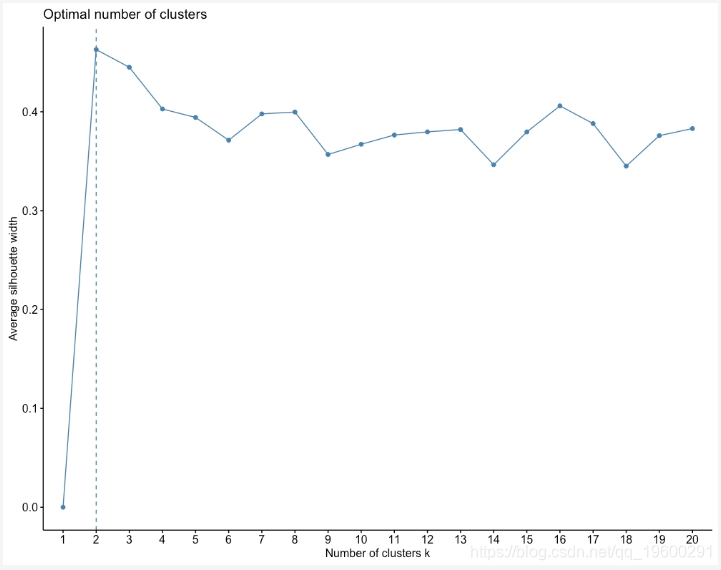
   图：聚类数与平均轮廓分数

WSS /肘法

为了识别数据集中的聚类，我们尝试最小化聚类中各点之间的距离，并且平方和（WSS）方法可以测量该距离  。WSS分数是集群中所有点的距离的平方的总和。

使用WSS确定群集数

在本练习中，我们将看到如何使用WSS确定集群数。执行以下步骤。

1. 将虹膜数据集的前两列（隔片长度和隔片宽度）放在  iris_data  变量中：

2. 导入  库

3. 绘制WSS与群集数量的图表

   输出如下：

4. 

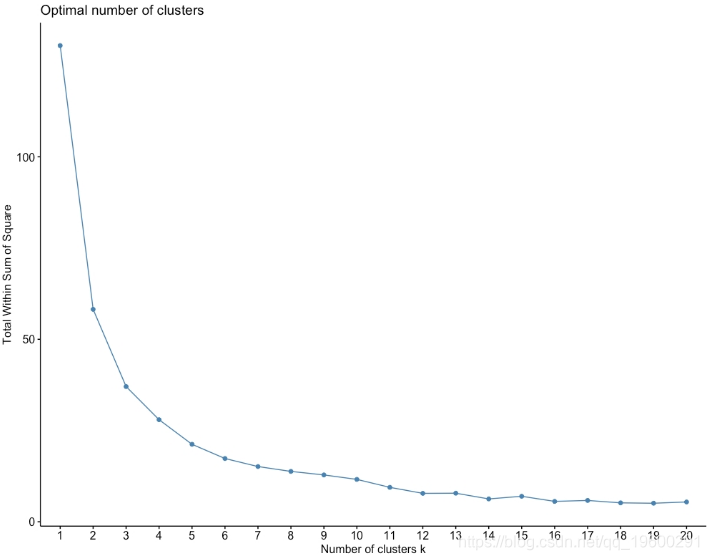
   图：WSS与群集数量

在前面的图形中，我们可以将图形的肘部选择为k = 3，因为在k = 3之后WSS的值开始下降得更慢。选择图表的肘部始终是一个主观选择，有时可能会选择k = 4或k = 2而不是k = 3，但是对于这张图表，很明显k> 5是不适合k的值，因为它们不是图形的肘部，而是图形的斜率急剧变化的地方。

差距统计

差距统计数据是在数据集中找到最佳聚类数的最有效方法之一。它适用于任何类型的聚类方法。通过比较我们观察到的数据集与没有明显聚类的参考数据集生成的聚类的WSS值，计算出Gap统计量。

因此，简而言之，Gap统计量用于测量观察到的数据集和随机数据集的WSS值，并找到观察到的数据集与随机数据集的偏差。为了找到理想的聚类数，我们选择k的值，该值使我们获得Gap统计量的最大值。

利用间隙统计量计算理想的簇数

在本练习中，我们将使用Gap统计信息计算理想的聚类数目：

1. 将Iris数据集的前两列（隔片长度和隔片宽度）放在  iris_data  变量中

2. 导入  factoextra  库

3. 绘制差距统计与集群数量（最多20个）的图表：

   

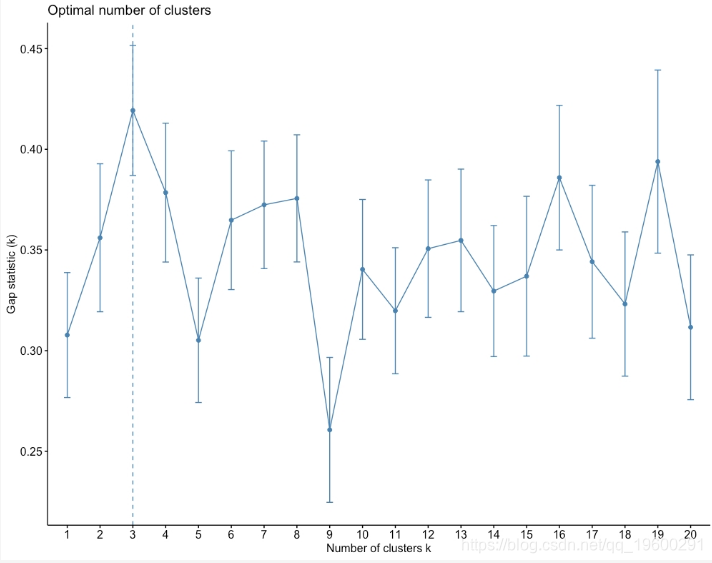
   图1.35：差距统计与集群数量

如上图所示，Gap统计量的最大值是k = 3。因此，数据集中理想的聚类数目为3。

找到理想的细分市场数量

使用上述所有三种方法在客户数据集中找到最佳聚类数量：

将变量中的批发客户数据集的第5列到第6列加载。

1. 用轮廓分数计算k均值聚类的最佳聚类数。

2. 用WSS分数计算k均值聚类的最佳聚类数。

3. 使用Gap统计量计算k均值聚类的最佳聚类数。

结果将是三个图表，分别代表轮廓得分，WSS得分和Gap统计量的最佳聚类数。