多目标关联(分配)最近邻法
- 最近邻数据关联
适用于两帧图片的中多目标位置关联,目标轨迹与新目标之间的关联、固定位置下的动目标跟踪关联等问题。
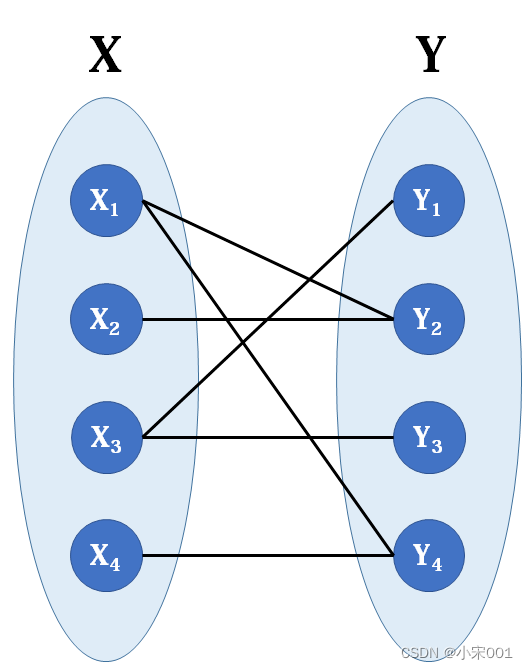
新目标与被跟踪目标的预测位置“最邻近”的观测点作为与航迹相关联的观测。
如有三批目标Tn和三个测量目标mn,所形成的关联矩阵为:
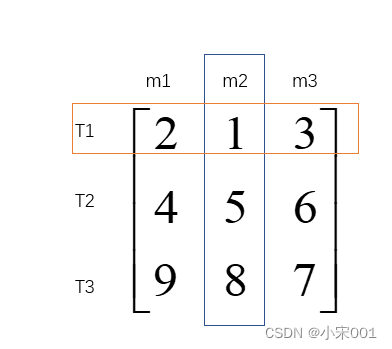
- m1,m2,m3表示关联矩阵每列,m1表示第一列,m2表示第二列,m3表示第三列,分别代表三个测量值。T1,T2,T3表示矩阵每行,T1表示第一行,T2表示第二行,T3表示第三行,分别代表三批目标值。
按最近邻分配结果: m2−>T1,m1−>T2,m3−>T3
注:测量与目标的分配是按最小值来分配的,分配完之后,则出掉那一行和那一列,剩下再按最小分配。
如:在关联矩阵中,第一行数字1最小,则配对,然后划掉矩阵第一行第二列,再看剩下的第二行中数字4最小,则再划掉第二行第一列,反复操作得到结果。
特点:一个目标最多只与跟踪门中一个测量相关,取跟踪门中距目标最近的测量与目标相关。
- 全局最邻近
使总的距离或关联代价达到最小,最优分配的问题
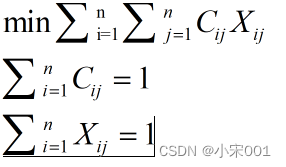
其中Xij为二值变量,为0表示不关联,为1表示关联,
Cij表示测量i与目标j之间距离。用矩阵表示时,矩阵的每行每列只能有一个元素为1.
例如:
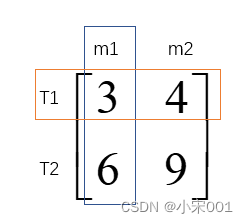
m1,m2表示关联矩阵第一列和第二列,代表2个测量数据,T1和T2表示关联数据第一行和第二行,代表2个目标。
关联结果:m2−>T1,m1−>T2,矩阵表示为:
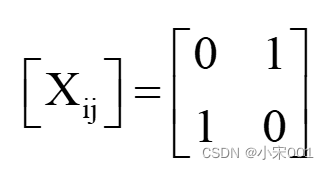
注:全局最近邻的关联结果即是在所有配对的结果中选取其总数最小的那一个。比如说第一个例子,有两种关联结果,第一种 m1−>T1,m2−>T2 ,3+9=12。 第二种 ,m2−>T1,m1−>T2 ,4+6=10。所以选择第二种关联结果。
关联矩阵较大时,二维分配的非NP问题可以选择使用匈牙利算法或者求解器进行求解。