0、摘要：

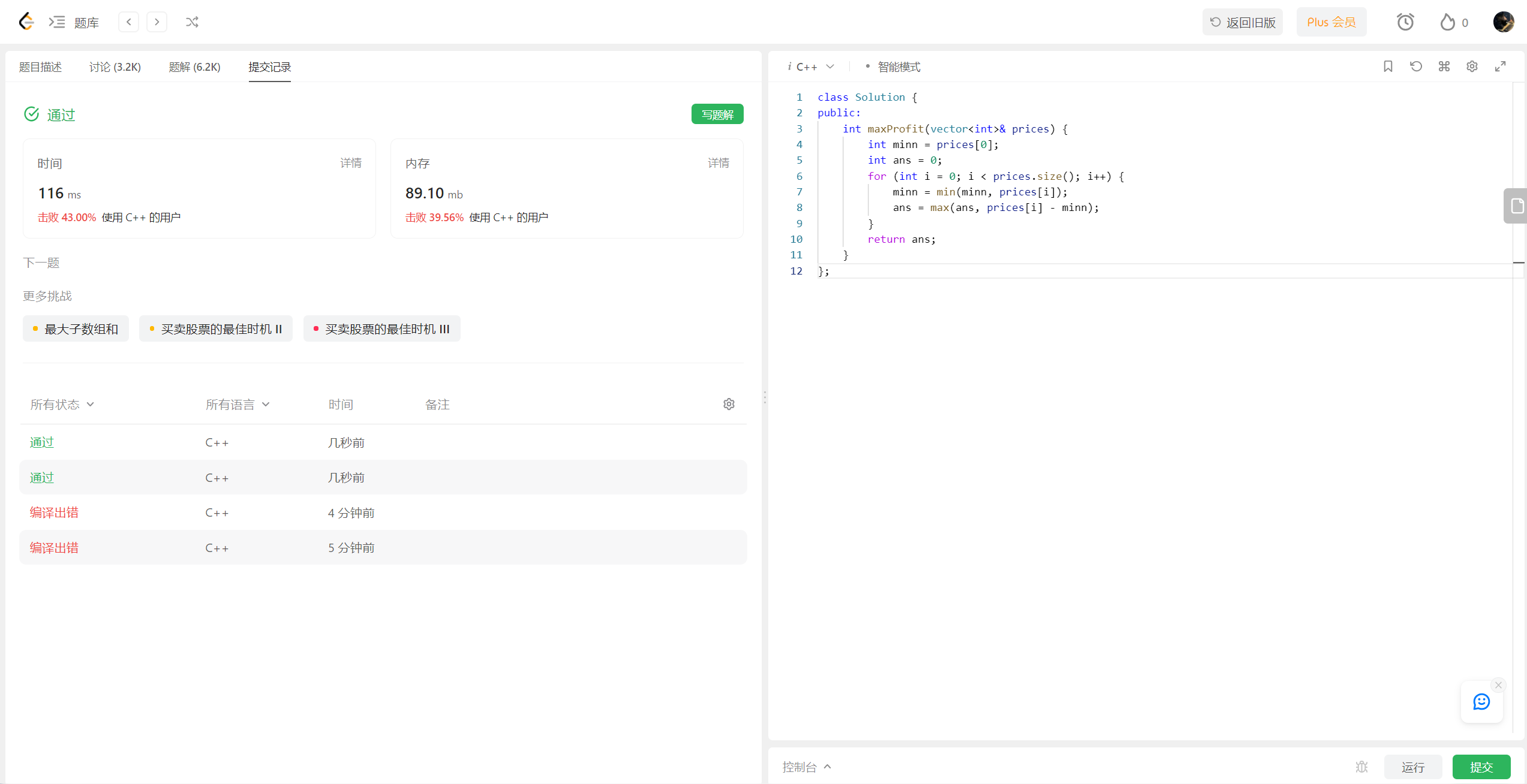
参考的文章提出了一种有效的不基于霍夫变换（HT）的随机圆检测算法（RCD）。提出的RCD的主要概念是，首先在图像中随机选择4个边缘像素，并定义一个距离准则来确定图像中是否存在可能的圆；在找到一个可能的圆后，应用证据收集过程来进一步确定可能的圆是否为真实的圆。对一些不同噪声水平的合成图像和一些含有一些遮挡圆和缺失边的圆形物体的真实图像进行了性能测试。实验结果表明，在光水平和中等水平之间的噪声水平上，所提出的RCD比其他基于HT的方法更快。对于高噪声水平，随机HT可能比提议的RCD更快，但以牺牲大量的内存需求为代价。

算法原理步骤
- 第一小节描述了所提出的RCD的基本思想。
- 第二小节展示了用于确定所选的四个边缘像素是否位于一个可能的圆上的距离准则。
- 第三小节描述了如何检查可能的圆是否为真实的圆，即所期望的圆。
- 第四小节展示所提出的RCD的形式化算法。

一、 Base Idea

设V表示图像中所有边缘像素的集合。在本文中，提出了一种非基于HT的随机圆检测算法。该算法算法每次随机选取4个边缘像素，并定义了一个距离准则来找到一个可能的圆。这种修改可以导致内存节省和计算效率的效果。如图1所示，四个边像素一般可以确定四个圆。
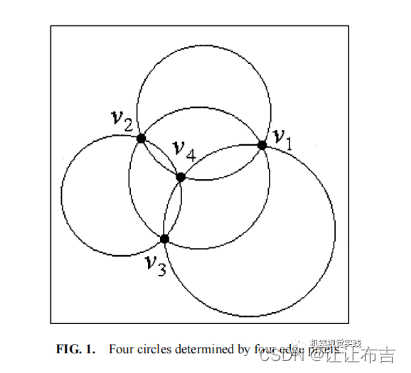
在这里插入图片描述

二、 Determining Possible Circle

将描述如何根据四个被选择的边缘像素来确定一个可能的圆。

2.1 判别条件

定义圆的表示方程：
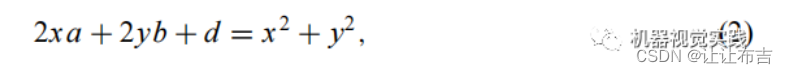
在这里插入图片描述
选取四个点中的三个点带入上面的公式中，并将其转换为矩阵形式，通过高斯消元法和克莱姆法则计算圆心和半径。在应用克莱姆法则时，因三个点是非线性关系，因此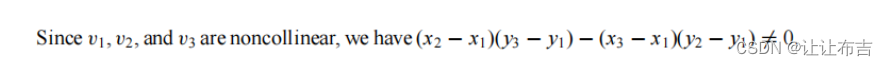
如果为0，则说明三点共线，不可能形成圆。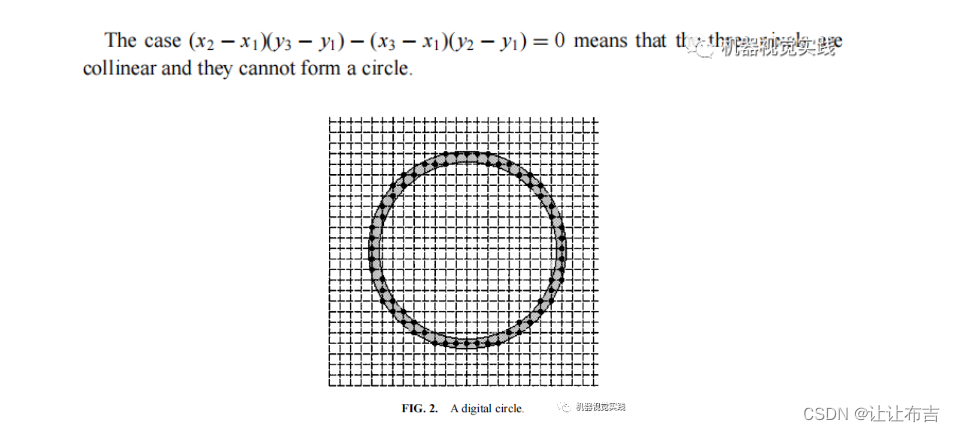在这里插入图片描述
计算第四个点到拟合圆心的距离，如果距离等于半径，说明该点在圆上。由于是数字图像，所以边缘像素很少恰好出现在一个圆上。因此，圆检测的目标是检测一组不精确而是大致位于数字圆上的边缘像素（见图2）。
在这里插入图片描述

2.2 圆的判别

依据上述内容，将四个点进行排列组合（4选3）拟合圆，并计算第四个点到圆心的距离，如果距离小于给定的距离阈值，则该圆可能是待求圆。
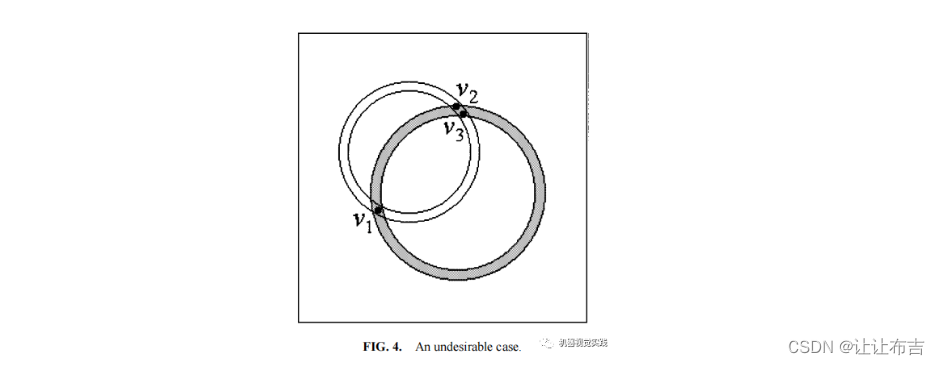
另一个弊端：其中两个圆太近，导致拟合的圆错误，如图4。为了避免这种情况，任意两个代理像素之间的距离必须大于给定的阈值Ta。如果是这样，这就意味着这三个代理像素有强有力的证据表明它们是可能的圆的代表。
在这里插入图片描述