重建二叉树

题目描述
给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。
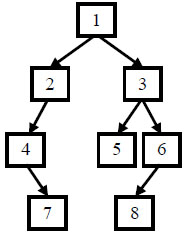
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

提示:
1.vin.length == pre.length
2.pre 和 vin 均无重复元素
3.vin出现的元素均出现在 pre里
4.只需要返回根结点，系统会自动输出整颗树做答案对比
数据范围：n≤2000，节点的值：−10000≤val≤10000
要求：空间复杂度 O(n)，时间复杂度 O(n)

思考了好几天没有想到解题方法，以下方案参考了大家的解题思路：

采用的方法：递归
递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程，最重要的就是查看能不能讲原本的问题分解为更小的子问题，这是使用递归的关键。

思路：二叉树的前序遍历，我们可以直到第一个元素是根节点，因为序列没有重复的元素，我们可以从中序遍历中找到根节点，将一个树分为左子树和右子树两个部分。
具体做法：

1. 先根据前序遍历第一个点构建根节点；
2. 然后根据中序遍历找到根节点在数组中的位置；
3. 再按照字数的节点数将两个遍历的序列分割成子数组，将子数组送入函数构建子树；
4. 直到子树的序列长度为0，结束递归。

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
#
# 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
#
# 
# @param preOrder int整型一维数组 
# @param vinOrder int整型一维数组 
# @return TreeNode类
#
class Solution:
    def reConstructBinaryTree(self , preOrder: List[int], vinOrder: List[int]) -> TreeNode:
        # write code here
        # 分别获取中序遍历和前序遍历的长度
        len_pre = len(preOrder)
        len_vin = len(vinOrder)
        # 判断这两个长度都不为0
        if len_pre == 0 or len_vin == 0:
        	return None
        # 构建根节点
        root = TreeNode(preOrder[0])
        
        # 从中序遍历中找到根节点所在的位置
        for i in range(len_vin):
        	if preOrder[0] == vinOrder[i]:
        		# 获取左子树的前序遍历
        		left_pre = preOrder[:i]
				# 获取左子树的中序遍历
				left_vin = vinOrder[1:i+1]
				# 构建左子树
				root.left = reConstructBinaryTree(left_pre, left_vin)
				# 获取右子树的前序遍历
				right_pre = preOrder[i+1:]
				# 获取右子树的中序遍历
				right_vin = vinOrder[i+1:]
				# 构建右子树
				root.right = reConstructBinaryTree(right_pre, right_vin)
				break
		return root