认识N( logN} 的排序

2.1归并排序
- 2.1.1代码实现归并排序
- - 2.1.1.1自己c++实现归并排序
  - 2.1.1.2gptc++实现归并排序
  - 2.1.1.3总结
  - 2.1.1.4比较行为
- 2.1.2归并排序使用master公式
- 2.1.3归并排序的扩展
- - 2.1.3.1小和问题
  - 2.1.3.2逆序对问题
2.2快排、荷兰国旗问题
- 2.2.1问题一
- 2.2.2问题二(荷兰国旗问题)
- - 2.2.2.1快排问题1.0
  - 2.2.2.2快排问题2.0
  - 2.2.2.3快排问题3.0

2.1归并排序

时间复杂度O(N*logN),额外空间复杂度O(N)

整体就是一个简单递归，左边排好序，右边排好序，让其整体有序
让其整体有序的过程里用了排外序方法
利用master公式来求解时间复杂度
归并排序的实质

二分，左边排好序，右边排好序，左1和右1比较，小的写入新内存，（如右1小，写入右1），左1和右2比较，（如右2小，写入右2），左1和右3比较，（如左1小，写入左1），此时新内存中为（右1，右2，左1），左2和右3比较……
在这里插入图片描述

2.1.1代码实现归并排序

2.1.1.1自己c++实现归并排序

自己实现c++代码

#include<iostream>
#include<vector>
#include<set>
#include<algorithm>
void print01(int val)
{
	std::cout << val << " ";
}
void test01()
{
	std::vector<int> Arr = { 5,6,9,4,2,3,7,5,6,8 };
	int length = Arr.size();
	std::multiset<int>Up;
	std::multiset<int>Down;
	if (length % 2 == 1)
	{
		for (int i = 0; i < (length + 1) / 2; i++)
		{
			std::vector<int>::iterator it = Arr.end()-1;
			Up.insert(*it);
			Arr.pop_back();
		}
		for (int j = 0; j < (length - 1) / 2; j++)
		{
			std::vector<int>::iterator it = Arr.end()-1;
			Down.insert(*it);
			Arr.pop_back();
		}
	}
	else
	{
		for (int i = 0; i < length / 2; i++)
		{
			std::vector<int>::iterator it = Arr.end()-1;
			Up.insert(*it);
			Arr.pop_back();
		}
		for (int i = 0; i < length / 2; i++)
		{
			std::vector<int>::iterator it = Arr.end()-1;
			Down.insert(*it);
			Arr.pop_back();
		}
	}
	
	std::vector<int>End;
	for (int q = 0; q < length; q++)
	{
		std::multiset<int>::iterator it1 = Up.begin();
		std::multiset<int>::iterator it2 = Down.begin();
		if (Up.size() != 0 && Down.size() != 0)
		{
			if (*it1 < *it2)
			{
				End.push_back(*it1);
				Up.erase(it1);
			}
			else
			{
				End.push_back(*it2);
				Down.erase(it2);
			}
		}
		else if(Up.size() != 0 || Down.size() != 0)
		{
			if (Up.size() != 0)
			{
				End.push_back(*it1);
				Up.erase(it1);
			}
			else
			{
				End.push_back(*it2);
				Down.erase(it2);
			}
		}
		else
		{
			break;
		}
	}

	for_each(End.begin(), End.end(),print01);
}
int main()
{
	test01();
	system("pause");
	return 0;
}

2.1.1.2gptc++实现归并排序

chatgpt实现

#include<iostream>
#include<set>
#include<algorithm>
#include<vector>

void print01(int val)
{
    std::cout << val << " ";
}

void test01()
{
    std::vector<int> Arr = { 5,6,9,4,2,3,7,5,6,8 };
    std::multiset<int> Up, Down;
    
    int length = Arr.size();
    int halfLength = (length + 1) / 2;
    
    for (int i = 0; i < halfLength; i++)
    {
        Up.insert(Arr.back());
        Arr.pop_back();
    }
    
    for (int i = 0; i < halfLength; i++)
    {
        Down.insert(Arr.back());
        Arr.pop_back();
    }

    std::vector<int> End;
    while (!Up.empty() && !Down.empty())
    {
        if (*Up.begin() < *Down.begin())
        {
            End.push_back(*Up.begin());
            Up.erase(Up.begin());
        }
        else
        {
            End.push_back(*Down.begin());
            Down.erase(Down.begin());
        }
    }

    // 处理剩下的元素
    for (const auto& val : Up)
    {
        End.push_back(val);
    }

    for (const auto& val : Down)
    {
        End.push_back(val);
    }

    std::for_each(End.begin(), End.end(), print01);
}

int main()
{
    test01();
    std::system("pause");
    return 0;
}

2.1.1.3总结

总结自己实现和gpt实现，给予gpt的要求是使用归并排序，减少代码行数
gpt没有使用迭代器来接收 Arr 中的值，将迭代器 it 初始化为 Arr 的最后一个元素的迭代器。而是直接使用Arr的迭代器begin

2.1.1.4比较行为

选择排序、冒泡排序、插入排序浪费了大量的比较行为
而归并排序虽然也进行了大量的比较，但是归并行为有效地利用对比，因为每一次比较行为都变成了有序的东西（有结果）

2.1.2归并排序使用master公式

master公式
T(N)=a* T(N/b)+O(N^d)
log(b,a)>d -> 复杂度为 O(N^log(b,a))
log(b,a)=d -> 复杂度为 O(N^d *logN)
log(b,a)< d -> 复杂度为 O(N^d)

logb^a<d 的时间复杂度O(N^d)
logb^a>d 的时间复杂度O(N^logb ^a )
logb^a==d 的时间复杂度O(Nd *logN)

上面例子中
T(N)=2T(N/2)+O(N),符合master公式
a=2,b=2,d=1
log2²==1,所以时间复杂度为O(N)

2.1.3归并排序的扩展

小和问题和逆序对问题

2.1.3.1小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和，求一个数组的小和
例：[1，3，4，2，5]1左边比1小的数，没有；3左边比3小的数，1；4左边比4小的数，1、3；2左边比2小的数，1；5左边比5小的数，1、3、4、2；所以小和为1+1+3+1+1+3+4+2=16

正常情况下时间复杂度为O(N²)

找寻更快的方法：
[1，3，4，2，5]1右边有4个数比1大14=4，3右边两个数比3大32=6,4右边1个数比4大14=4，2右边1个数比2大21=2；4+6+4+2=16
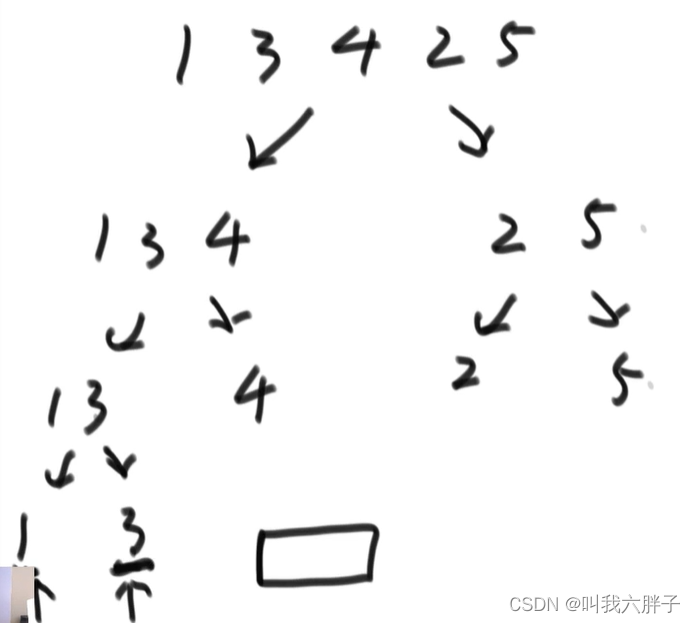
请添加图片描述
1，3对比产生1个1。返回排序13（排序，从小到大）
1，4对比产生1个1，3。4对比产生1个3，1，3，4.返回排序134

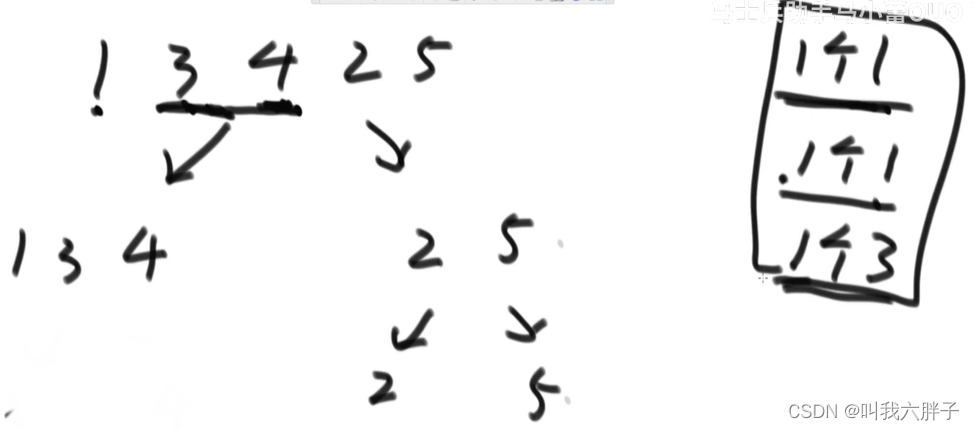
2，5对比产生1个2，返回排序25

134中指向1，25中指向2，对比产生2个1，拷贝1
134中指向3，25中指向2，对比3大，拷贝2，25中指向5，对比产生1个3，拷贝3
134中指向4，25中指向2，对比4大，25中指向5，对比产生1个4，拷贝4，拷贝5
12345
小和1+1+3+2+2+3+4=16

1和2对比产生的2个1不是通过遍历找到的2，而是直接通过下标begin() 和end()找到

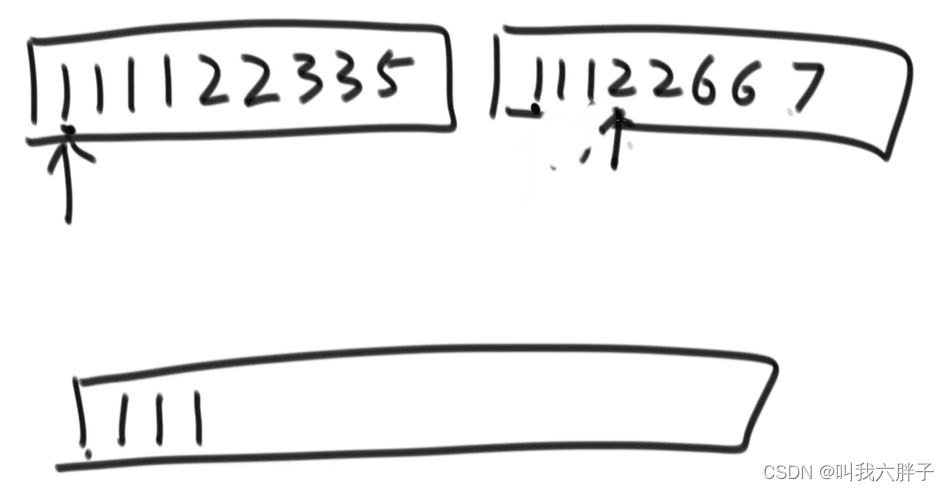
请添加图片描述
如图情况左右相对，一定要先拷贝右组的数，而不是左组

2.1.3.2逆序对问题

在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序对

例：3，2，4，5，0
32，30，20，40，50

2.2快排、荷兰国旗问题

2.2.1问题一

给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度0(N)

35674358 num=5
准备一个变量i
情况a，[i]<=num,[i]和<=区的下一个数交换，<=区右扩，i++
情况b，[i]>num,i++
3和num5比较，num5大，情况a执行
5和num5比较，等于num5，情况a执行
6和num5比较，6大，情况b执行
……

2.2.2问题二(荷兰国旗问题)

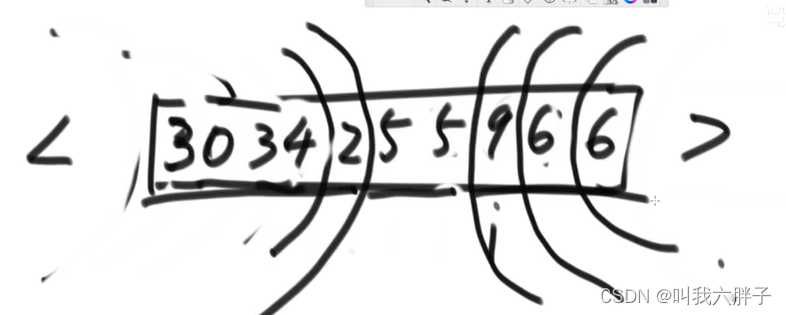
给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度O(N)

35674358 num=5
准备一个变量i
情况a，[i]<num,[i]和<区的下一个数交换，<区右扩，i++
情况b，[i]>num,[i]和>区的上一个数交换，>区左扩，i不动
情况c，[i]==num,i++
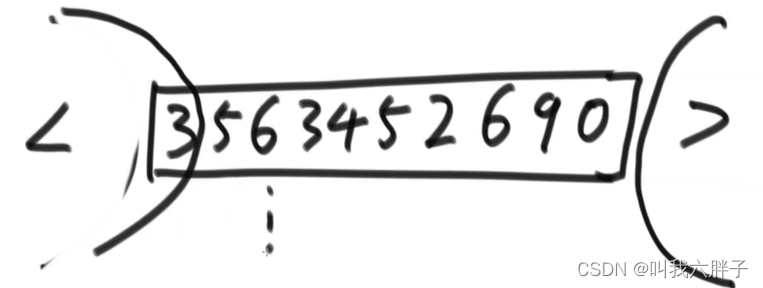
请添加图片描述

2.2.2.1快排问题1.0

时间复杂度O(N²)

在一串数里，拿最后一个数作为num，<=num放左边，>=num放右边，num和>=num区域的第一个数做交换。再次重复，取新的最后一个数num

2.2.2.2快排问题2.0

时间复杂度O(N²)
最好的情况为T(N)=2T(N/2)+O(N) , 时间复杂度为O(N*logN)
最坏的情况没有左侧部分或右侧部分，时间复杂度O(N²)

在一串数里，拿最后一个数作为num，<num放左边，>num放右边，==num放中间，最后一个数和>5区域第一个数交换。在<num，>num区域做递归

分析：
快排2.0比快排1.0稍快，因为快排2.0一次搞定一批数
划分值越靠近两侧，复杂度越高；划分之越靠近中间，复杂度越低
可以轻而易举的举出最差的例子，所以不改进的快速排序时间复杂度为O(N^2)
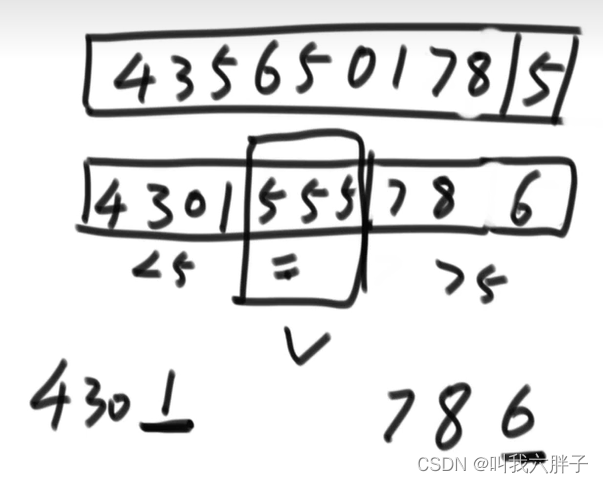
请添加图片描述
4356501785，取尾数5为num值，排序出三个区域
<5 ,=5 ,>5 5
尾数5和>5区域的第一个数互换
<5 （4301）,=5（555） ,>5（786）
4301取尾数1，排序出三个区域
<1 （0）,=1 （）,>1（43），1
0 1 43
43取尾数3，排出三个区域……
786取尾数6，排序出三个区域
<6 （） ,=6 （） ,>6（78）， 6
6 78
78取尾数8，排出三个区域……

2.2.2.3快排问题3.0

请添加图片描述
L到R位置上，随机取一个数，和最后一个数交换，然后用此数做划分
原理：
有可能
T(N)=T(N/5)+T(4/5*N)+O(N)
T(N)=T(N/3)+T(2N/3)+O(N)
T(N)=2T(N/2)+O(N)
T(N)=T(4N/5)+T(N/5)+O(N)
…………
所有情况都是等概率1/n的，所以汇总所有可能，把所有式子求概率累加，再求数学长期期望，得出结果O(N * logN)