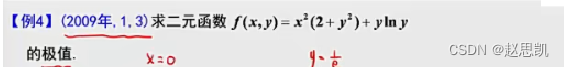目录

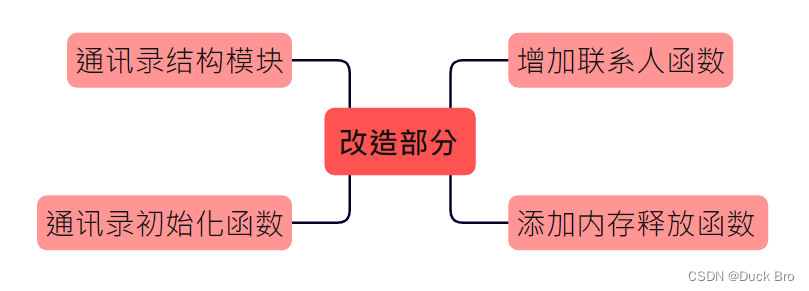
 无约束极值

极值的必要条件

驻点和极值点的关系

多元函数极值点可能取的点：

极值的充分条件

 条件极值与拉格朗日乘数法

 最大最小值

例题

例题1：

例题2：

 ​编辑

 例题3：

例题4：

 ​编辑

 例题5：

 例题6：

---

 

 无约束极值

 无约束极值的定义和普通的极值类似：在一个定点的去心领域内，如果这个定点对应的值始终大于等于邻域内部的所有值，那这一点就称为极大值，极小值的定义也是如此。

极值的必要条件

 如果函数在一定点内存在偏导数，并且这一点是函数的极值点，那么这一点的偏导数都等于0.

驻点和极值点的关系

驻点和极值点只有唯一一个关系：可导函数的驻点一定是极值点。

可偏导函数的驻点一定是极值点。

多元函数极值点可能取的点：

 可能的极值点可以分为两种：驻点或者至少一个偏导数不存在的点。

极值的充分条件

 

 简单的理解：二阶连续偏导数存在，两个一阶偏导数等于0，记A为对x的二阶偏导数，记B为对x和对y分别求一次偏导数，记C为对y的二阶偏导数。

如果AC-B^2小于0，没有极值点

等于0，不一定。

大于0，存在极值点，当A小于0时是极大值，当A大于0时是极小值。

 条件极值与拉格朗日乘数法

 最大最小值

 求驻点以及偏导数至少有一个不存在的点，然后求出边界上的最大最小值，比较得出最大值与最小值。

例题

例题1：

 

例题2：

 

 

 例题3：

 ​​​​​​​​​​​​​​

例题4：

 

 

 例题5：

 例题6：